精英数学大视野：第29讲抽屉原理与数学刺绣

在数学上,“包络”是指一系列的直线或曲线包围出另一个形状的情形,如左图中若干条直线组成了心脏线、抛物线．

20世纪初,西方的数学书上讲述了用直线画曲线的各种画法,当时形成了“数学刺绣”的时尚．

知能概述

若把8个物体放入7个抽屉,则一定有一个抽屉放了2个或2个以上的物体;若把8个物体放入2个抽屉,则一定有一个抽屉放了4个或4个以上的物体;若把8个物体放入3个抽屉,则一定有一个抽屉放了3个或3个以上的物体．

我们把“物体数与抽屉数”的关系概括为数学上的一个原理,即“抽屉原理”．抽屉原理的常用形式是:

原理1　把(n＋1)个元素放入n个抽屉,则一定有一个抽屉有两个或两个以上的元素．

原理2　把m个元素放入n(n＞1,m＞n)个抽屉,则一定有一个抽屉至少有k个元素,其中:

问题解决

例1　1011人参加考试,总得分为50501分(百分制),则至少有_________人的考试成绩是相同的．

(天津市竞赛题)

数学发明创造的动力不是推理,而是想象力的发挥．

——德·摩根

互素的判定

当代著名数学家厄尔多斯听说一个叫波萨的小孩很聪明,1959年就问了一个问题加以考察:

如果你有n＋1个正整数,这些正整数小于或等于2n,那么,你一定会有一对整数是互素的,你知道这是什么原因吗?

解题思路　把不同得分分别作为抽屉,参加考试的考生1011人视作元素．

例2　夏令营组织1995名营员去游览故宫、景山公园、北海公园,规定每人最少去一处,最多去两地游览,那么至少有(　)人游览的地方完全相同．

A．665　B．499　C．333　D．332

(北京市“迎春杯”竞赛题)

解题思路　把游览方式作为抽屉．

例3　从1到100这100个自然数中任取51个,求证:其中必有两个数,它们的差是50．

(上海市竞赛题)

解题思路　需构造50个抽屉,把1到100这100个自然数恰当分组．

例4　一副扑克牌有4种花色,每种花色有13张,从中任意抽牌．问:最少要抽多少张牌,才能保证有4张牌是同一花色的?

(“华罗庚金杯”少年数学邀请赛试题)

解题思路　将花色作为“抽屉”,现有4个“抽屉”,牌作为“元素”,要保证有4个“元素”在一个“抽屉”里,至少要多少个“元素”,即＝4,求m＝?

例5　任意给出五个整数,证明:必能从其中选出三个整数,使得它们的和能被3整除．

分析　任意一个整数被3除后余数或是0,或是1,或是2,可以利用五个整数被3除以后的余数进行分类,制造抽屉．

抽屉原理又称为鸽笼原理,它是德国数学家狄利克雷首先提出来的,因此也称为狄利克雷原理．这一原理对于解决数学中一些具有特殊性质的对象的存在问题,通常称为存在性问题,是一种强有力的工具．

运用抽屉原理解题的一般步骤是:

(1)指出元素,构造抽屉;

(2)把元素放入或取出抽屉;

(3)说明理由,推出结论．

能否合理、正确地制造出“抽屉”,是运用抽屉原理解决问题的关键．

证明　任一整数被3除后余数只有0,1,2三种可能,把余数0,1,2看作三个抽屉,则这五个数中至少有二个数被3除后有相同的余数．

(1)若每个抽屉均不空,则三个抽屉中各取一个数,这三个数被3除的余数分别为0,1,2,显然这三个整数的和能被3整除．

(2)若有一个抽屉是空着的,则五个整数放入二个抽屉,由抽屉原理可知,至少有一个抽屉有三个或三个以上的数,取这抽屉中的三个数,其和显然能被3整除．

综合(1)(2),本题得证．

例6　在一个边长为1的正方形内,任意给定9个点．证明:在以这些点为顶点的各个三角形中,必有一个三角形的面积不大于．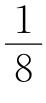

(江苏省竞赛题)

分析与解　以边长为1的正方形面积为12＝1(面积单位),三点A,B,C组成的三角形ABC面积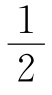＝×底×高≤,则这种三角形的底边长和高的乘积不大于,因而问题转化为9个点中至少有三个点落在面积为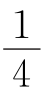的正方形的一个小区域内,以此来设计抽屉．

如图①、②,把正方形分成四个全等的正方形或小长方形,将每个小正方形或长方形看成抽屉,则9个点放入4个抽屉中,至少有一个抽屉,其中至少有3个点,设为A,B,C,则三角形ABC的面积≤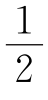×(小正方形或小长方形的面积)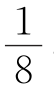＝,证毕．

例7　一个书架从上到下依次有五层,把15册书放到书架的各层上,有些层上可以不放．

求证:无论怎样放,在书架上每层图书的册数以及每相邻两层的图书册数之和中,至少有两个是相等的．

(浙江省竞赛题)

分析　初看题目,会觉得每层摆放图书册数的可能性太多,也是问题不易解决的主要障碍．

首先,如果有一层不放图书,不妨设第二层不放图书,那么第二、三层图书册数之和与第三层图书册数相等,命题成立．

其次,如果每层都放了图书,且有两层图书册数相等,显然命题也成立．

排除上述两种情况,各层图书册数只有唯一的可能性:1,2,3,4,5．

解与整数相关问题,构造抽屉的基本方式有:

(1)利用奇偶性构造;

(2)用剩余类构造;

(3)用数组构造,即把符合条件的数放在一起,组成一个数组,将这些数组作为抽屉．

等分图形、染色图形,是运用抽屉原理解几何问题,构造抽屉的常用方法．

证明　如果有任何两层图书册数相同,或有任何一层不放图书,本题结论显然成立．否则,各层图书册数只有唯一的可能性:1,2,3,4,5(但不一定顺次)．

设五层图书的册数依次为a,b,c,d,e,考虑a,b,c,d,e,a＋b,b＋c,c＋d,d＋e这9个数,最大的可能是9,最小的可能是1．

如果上述9个数中有某一个数为9,则必是由4＋5构成．此时,无论怎样放,都不会同时出现8册和7册,因此上述9个数只有8种可能,根据抽屉原理1,必有两个数相等．

云深不知处

许多科学论断只能确定现象或对象的存在,但不能指出存在的位置、证明存在的时刻、给出具体的样本．

抽屉原理、代数基本定理等都是纯粹存在性的定理．

“只在此山中,云深不知处”,贾岛诗句应是存在性定理最形象的描述．

例8　证明:任何6个人中,必有3个人互相认识,或者有3个人互相不认识．

(匈牙利数学竞赛题)

借助图形表示这一抽象的思想．

分析　用点A1,A2,…,A6代表6个人,两个人互相认识则在对应的两点间连一条红边,否则连一条蓝边,问题转化为图中必有三边同色的三角形．

证明　考虑A1与5条引线,因为只染了两种颜色,由抽屉原理知必有3条同色．不妨设A1A2,A1A3,A1A4同为红色;若A2A3,A3A4,A4A2中有红边,则有红色△A1AiAj(2≤i,j≤4);若A2A3,A3A4,A4A2无红边,则△A2A3A4为蓝色三角形．无论哪种情况,图中都有同色三角形．

例8是著名的同色三角形问题,本题也可以换一种说法:

平面上有A,B,C,D,E,F6个点,其中没有3点共线．每两点之间都用红线或蓝线连接．求证:不管怎样连接,至少存在一个三边同色的三角形．

此后几十年中这个问题被许多国家反复改造、变形、推广后用作竞赛题,如:

平面上有6点,任何3点都是一个不等边三角形的顶点,求证:这些三角形中一个的最短边同时是另一个三角形的最长边．(波兰数学竞赛题)

1．某校七年级有3个班,在一次数学竞赛中至少有________人获奖才能保证在获奖的同学中一定有4名学生同班．

(吉林省竞赛题)

2．新年晚会上,老师让每位同学从一个装有许多球的口袋中摸出两个球,这些球给人的手感都相同,只有红、蓝、黄、白、绿五种颜色之分(摸时看不到颜色),结果发现总有2人取的球的颜色完全相同,由此可知参加取球的人至少有_________人．

(“希望杯”邀请赛试题)

3．在8×8的方格纸中,每个方格内可以填上1～4四个自然数中任意一个,填满后,对每个2×2“田”字形内的4个自然数求和,在这些和中,相同的和至少有_________个．

(江苏省探索与应用能力竞赛题)

4．要在20米长的阳台上放上11盆花,不管怎么放,至少有_________盆之间距离不超过2米．

5．现有145颗棒棒糖,分给若干小朋友,不管怎样分,都至少有1个小朋友分到5颗或5颗以上,这些小朋友的人数最多有_________个．

(河南省竞赛题)

6．从117,118,119,…,2011,2012这1896个数中,至少要取出_________个不同的奇数,才能保证取出的数中一定存在和为2010的两个奇数．

(世界数学团体锦标赛试题)

7．18个小朋友中,(　)小朋友在同一个月出生．

A．恰好有2个　B．至少有2个　C．有7个　D．至多有7个

8．在边长为2厘米的等边三角形内随意取一些点,如果保证所取的点中一定存在距离小于1厘米的两点,那么取的点至少应有(　)．

A．4个　B．5个　C．6个　D．7个

(江苏省竞赛题)

9．有n个人报名参加甲、乙、丙、丁四项体育比赛活动,规定每人至少参加一项比赛,至多参加两项比赛,但乙、丙两项比赛不能同时兼报．若在所有不同的报名方式中,必存在一种方式至少有20个人报名,则n的最小值等于(　)．

A．171　B．172　C．180　D．181

(天津市竞赛题)

10．从1,2,…,2012中挑选一些数,其中没有两数之和能被其差整除,选出的这些数最多有(　)．

A．671个　B．672个

C．673个　D．以上都不对

(北京大学自主招生试题)

11．在1,4,7,10,13,…,97,100中任选20个不同的数,其中至少有4个不同的数a,b,c,d,使得a＋b＝c＋d＝104．

(美国普特南大学生数学竞赛题)

12．在100个连续自然数1,2,…,100中,任取51个数．证明:这51个数中一定有两个数,其中一个是另一个的倍数．

(莫斯科市竞赛题)

13．在10×10方格表中,若其中两个方格至少有一个公共顶点,则称这两个方格是“友好的”．将方格表中的每个方格填入小于或等于10的正整数,使得互为友好的方格中的数互素．证明:在方格表中,某些数出现的次数至少是17次．

(克罗地亚竞赛题)

14．一群小朋友购买售价是3元和5元的两种商品．每人购买的数量最少是一件,他们也可购买相同的商品,但每人的购买总金额不得超过15元,若小朋友中至少有三人购买的两种商品的数量完全相同,问这群小朋友最少有多少人?

(“华罗庚金杯”香港中学竞赛题)

15．在1,2,3,…,90,91这91个自然数中任取k个数,使得其中必有两个自然数p,q,满足,试确定自然数k的最小值,并说明理由．

(北京市竞赛题)

16．在边长为1的正方形内任取五个点,证明:总可以找到两点,它们之间的距离不大于正方形对角线长的一半．

(美国普特南大学生数学竞赛题)

17．有一列数,前两个数是1,2,从第三个数起,每个数都等于它前面相邻的两个数的和的个位数字,请回答以下问题:

(1)在这列数中能否依次出现相邻的2,0,1,2这四个数?说明理由．

(2)这列数中的第2012个数字是什么?说明理由．

(“希望杯”邀请赛试题)

18．从正35边形中选出15个顶点染为红色．问:对于任何一种染法,是否均能找到三个被染红的点,使得以这三个点为顶点的三角形是等腰三角形?

(德国数学竞赛题)

例1　11　把得分0,1,2,…,99,100分别作成101个抽屉,参加考试的考生1011视作元素,根据抽屉原理,一定有一个抽屉至少有＋1＝11个元素,即至少有11个人有相同的分数．

例2　C　营员游览方式有6种:故宫;景山公园;北海公园;故宫、景山公园;故宫、北海公园;北海公园、景山公园．将这6种游览方式视作6个抽屉,1995名营员视作元素,根据抽屉原理,至少有一个抽屉里至少有＋1＝333个元素,则至少有333人游览的地方完全相同．

例3　将1到100这100个自然数分成50组如下:{100,50},{99,49},{98,48},…,{51,1}．每一组中有两个数,它们的差恰好是50,将这50个组作为抽屉,任取的51个数中至少有2个数来自同一抽屉,这两个数的差就是50．

例4　在抽出13张牌时,由抽屉原理,至少有一种花色的牌张数≥＋1＝4,即有4张牌是同一花色的,另一方面,如果只抽出12张牌,可能每种花色恰好3张,故最少要抽13张牌．

1．10　3×(4－1)＋1＝10,故至少要有10名学生获奖才能保证一定有4名获奖学生是同班的．

2．16　颜色相同或不同的情形有15种,至少有16人参加摸球时,就能保证有＋1＝2人摸出的两球的颜色完全相同．

3．4　在8×8方格纸中,共有2×2的“田”字形7×7＝49个,在1～4中任取4个数(可重复)的和可以是4～16,共13种可能,49÷13＝3……10,根据抽屉原理,至少有3＋1＝4个“田”字形内的数字之和是相同的．

4．2　只要把阳台划分成每段2米的小间隔,这样共得10个小间隔,11盆花放入这10个小间隔,至少有2盆放入同一个小间隔内,这两盆花的距离不超过2米．

5．36　设最多有x个小朋友,这相当于x个抽屉,问题变为把145颗糖放进x个抽屉,至少有1个抽屉放了5颗或5颗以上,则4x＋1≤145,解得x≤36,所以小朋友的人数最多有36个．

6．504　从已知的1896个数中选出和为2010的两个奇数,共有如下444种情形:117＋1893,119＋1891,121＋1889,…,1003＋1007．

由抽屉原理可知,从117,119,121,…,1891,1893这889个数中,至少要取出445个不同的奇数,才能保证取出的数中一定存在两个和为2010的奇数．

又1894,1895,1896,…,2011,2012中共有(2012－1894)÷2＝59个奇数,

所以从117,118,119,…,2011,2012这1896个数中,至少要取出445＋59＝504个不同的奇数,才能保证取出的数中一定存在两个和为2010的奇数．

7．B

8．B　连该等边三角形三边的中点,将其分割为4个边长均为1厘米的等边三角形,以此作为抽屉．

9．B　用有序数组(a甲,b乙,c丙,d丁)表示每个人报名参加甲、乙、丙、丁四项体育比赛的方式,其中,若参加某项比赛,则相应的数记为1(如参加甲项比赛,则记a甲＝1),否则,相应的数记为0．

于是,每个人报名参赛的方式共有9种可能:

(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(1,1,0,0),(1,0,1,0),(1,0,0,1),(0,1,0,1),(0,0,1,1)．

故n个人共有9种报名参赛方式,以此作为9个抽屉．

由抽屉原理,知当n＝19×9＋r(r≥1)时,必有一种方式至少有20个人报名．

所以,当r＝1时,n取最小值19×9＋1＝172．

10．A　所有3k＋1型数有＋1＝671个,且满足任意两数之和不能被其差整除(因为其差能被3整除)．

若取数超过671个,则由抽屉原理知有两数之差为1或者2．

当两数之差为1时,两数之和能被其差整除;

当两数之差为2时,两数同奇偶,因此两数之和能被其差整除．

11．1,4,7,10,13,…,97,100共34个数,去掉1和52,其余的32个数配成16对;{4,100},{7,97},{10,94},…,{49,55}．所取的20个数中至少有20－2＝18个数选自上述16个数对．由抽屉原理知:其中必有两个数a,b选自同一个数对,它们的和a＋b＝104,剩下的18－2＝16个数选自剩下的16－1＝15个数对,同理知其中必有两个数c,d选自同一个数对,它们的和c＋d＝104．

12．因为自然数不是奇数就是偶数,二者必居其一,而任何偶数又必定能表示成:奇数×2n(其中n＝1,2,…)．

例如,16＝1×24,24＝3×23,100＝25×22．

因此,我们将1～100的全部自然数按奇数和奇数×2n分成下面50个组,每组的代号为Mi(i＝1,2,3,…,50),即

M1＝{1,1×21,1×22,1×23,1×24,1×25,1×26};

M2＝{3,3×21,3×22,3×23,3×24,3×25};

M3＝{5,5×21,5×22,5×23,5×24};

M4＝{7,7×21,7×22,7×23};

…

M49＝{97};M50＝{99}．

这样分类,很明显可以把1,2,…,100这100个自然数既无遗漏又不重复地分放在50个组Mi中,因此,不论用何种方式从中取出51个数时,必有两个数来自同一组,而在同一组中的任何两个数,其中的一个必然是另一个的整数倍．

13．将10×10方格表划分为25个2×2个子格表,在每个子格表中,至多有一个偶数,且至多有一个数可被3整除．因此,在此方格表中,至多有50个数可被2或3整除．于是,至少剩下50个数,且其中的每一个数为1,5或7．由抽屉原理知:其中至少一个数出现的次数不少于17次．

14．设购买3元商品a件,5元商品b件,则(a,b)只可能为(1,0),(2,0),(3,0),(4,0),(5,0),(0,1),(1,1),(2,1),(3,1),(0,2),(1,2),(0,3),共有12种购买组合．由抽屉原理可知人数至少有2×12＋1＝25．

15．将1～91这91个自然数分为9组,使每组中任两个自然数的比值均不小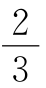于且不大于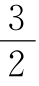,分组法如下:

A1＝{1};

A2＝{2,3};

A3＝{4,5,6};

A4＝{7,8,9,10};

A5＝{11,12,13,14,15,16};

A6＝{17,18,…,25};

A7＝{26,27,28,…,39};

A8＝{40,41,…,60};

A9＝{61,62,…,91}．

这样,1～91这91个自然数全部分放在这9个抽屉之中,而且同一抽屉中的任何两数之比的比值一定介于和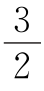之间．现从前91个自然数中任取10个数,必有两个数出于同一抽屉,因而命题成立,故k的最小值是10．

16．连接正方形两组对边的中点,得到四个小正方形——四只“抽屉”,由抽屉原理,必有一只“抽屉”里至少有两点,所以它们的距离不大于正方形对角线长的一半．

17．(1)否．假设能出现,则因为2＋0＝2,而2≠1,于是矛盾,故不会有2,0,1,2连续出现的情形．

(2)注意到数串出现的只是0到9的数字,其中5个奇数,5个偶数,所以不同的(奇,偶)对共有5×5＝25对,因此,根据抽屉原理,(奇,偶)对在这无穷数串中必定会重复出现,此后成周期循环．我们通过实验找规律:

我们发现,第61个数等于第1个数,第62个数等于第2个数,以下各数以60为周期循环出现．

因为2012÷60＝33……32,所以这列数中的第2012个数字等于第32个数字,即8．

18．对于任何一种染法均能找到三个被染红的点,使得以这三个点为顶点的三角形是等腰三角形．

易证明:对于任何一个正五边形,从其顶点中任意选出三个顶点,且以这三点为顶点的三角形必是等腰三角形．

于是,对于该正35边形,不妨设其顶点按顺时针方向依次为A1,A2,…A35,将Ai、Ai＋7、Ai＋14、Ai＋21、Ai＋28(i＝1,2,…,7)这五个点分成一组,共七组．

据抽屉原理,知当从正35边形的顶点中选出15个时,必有一组中选出了＋1＝3个点．而同一组中的五个点恰构成一个正五边形的顶点,因此,以这三点为顶点的三角形恰是等腰三角形．