七年级2020数学精英视野28讲：几何计数方法与规律总结

飞鸟、彩蝶、鱼、骑士,栩栩如生,妙手天成．数学艺术家埃舍尔是荷兰的一位版画大师,他在20世纪四五十年代创作了许多用单一的精美图形铺满平面的图案奇作．他的作品以优美的外表、丰富的内涵、浓郁的数学韵味而闻名于世．

知能概述

几何计数,即求满足一定条件的图形的个数．由于组合图形位置关系的多样性,常产生多个符合条件的图形且图形易重复或遗漏．解几何计数问题常用到以下方法原理:

1．分类穷举:即根据对象的特征,把它分成若干类,再一个一个地数出来．

2．分解转化:即把复杂的图形分解为常见的基本图形．

3．代数计算:即依据图形的特征规律,通过列代数式、方程、递推式等代数方法计算．

4．利用加法原理、乘法原理．

加法原理:做一件事,完成它有n类方法,在每类方法中分别有m1,m2,…,mn种不同的方法,那么完成这件事共有m1＋m2＋…＋mn种不同的方法．

乘法原理:做一件事,完成它需要分成n个步骤,在每步中分别有m1,m2,…,mn种不同的方法,那么完成这件事共有m1·m2·…·mn种不同的方法．

问题解决

例1　如果依次用a1,a2,a3,a4分别表示图①,②,③,④中的三角形个数,那么a1＝3,a2＝8,a3＝15,a4＝_________．如果按照上述规律继续画图,那么a9与a8之间的关系是:a9＝a8＋________．

(江苏省竞赛题)

我坚定地认为,任何一门自然科学,只有当它能应用数学工具进行研究时,才能算是一门发展渐趋完善的真实科学．

——康德

17线的交点

傅立叶(1768—1830),法国著名数学家,其主要成就是对热传导问题的研究,以及为此研究而引入的数学方法(傅立叶级数)．

一次,他写信给他的老师、朋友波纳,信中提出下面一个问题:

在平面上作17条直线,使它们交点总数为101个,这办得到吗?

解题思路　对几种简单情形进行分析,然后从中归纳猜想出一般的规律．

例2　图中可数出的平行四边形的个数为(　)．

A．123　B．114

C．108　D．105

(“五羊杯”竞赛题)

解题思路　m×n长方形棋盘可数出长方形(1＋2＋…＋m)×(1＋2＋…＋n)个,这是解本例的基础,注意图中两处重叠现象．

例3　将一个圆形纸片用直线划分成大小不限的若干小纸片,如果要分成不少于2003个小纸片,至少要画多少条直线?请说明理由．

(浙江省竞赛题)

解题思路　设至少要画n条直线,要使直线最少,应使n条直线将圆分成的块数最多,解题的关键是建立n的关系式．

有些几何计数问题可转化为方程、不定方程、不等式来求解,通过确定方程解的个数、不定方程整数解的个数或确定某个几何元素的取值范围来求解．

例4　已知三角形的三边长都是整数,最大边长为8,求满足这样条件的互不全等的三角形的个数．

(河南省竞赛题)

解题思路　确定三角形另两边中一边的取值范围,就可枚举计数．

例5　如图,在2×3的矩形方格纸上,各个小正方形的顶点称为格点．问:以格点为顶点的等腰直角三角形共有多少个?

(全国初中数学联赛题)

分析与解　等腰直角三角形有怎样的几何特征?这一问题的牵引,是解题“从何处入手”的一个切入点．三角形的一个内角为90°(显性或隐性),其两条夹边相等;三角形三边a,a,c,a2＋a2＝c2,即c＝;最大边的中垂线不通过格点的三角形一定不是等腰直角三角形,但反之不一定成立．

以格点为顶点的线段长度可取8个数值:,．以这些线段组成的等腰直角三角形按三边长来考虑可以分为以下四种情况:和,下面按斜边长分四类来进行计数．

(1)当斜边长为2时,斜边一定是小正方形的对角线,这样的线段有12条,每条这样的线段对应着两个等腰直角三角形,共有2×12＝24(个)．

(2)当斜边长为2时,图形中长为2的线段有10条,其中有6条在2×3矩形的四周上,每条这样的线段对应着一个等腰直角三角形;另有4条在2×3矩形的内部,每条这样的线段对应着两个等腰直角三角形,共有6＋2×4＝14(个)．

(3)当斜边长为2时,斜边一定是2×2正方形的对角线,这样的线段有4条,每条这样的线段对应着两个等腰直角三角形,共有2×4＝8(个)．

(4)当斜边长为时,这样的线段有4条,每条这样的线段对应着一个等腰直角三角形,共有4个．

故以格点为顶点的等腰直角三角形的个数为24＋14＋8＋4＝50(个)．

例5有效地考查思维的严谨性与清晰性．

思维的严谨性表现在:分类计算不重、不漏、不假,既不重复地不遗漏地计算等腰直角三角形,更不把非等腰直角三角形计算在内;

思维的清晰性表现在:构思一个层次分明的求解程序,逐层深入地进行几何图形的结构分析,逻辑清晰地进行分类．

思维的清晰与严密源于细致与坚韧,细节是一种长期潜心的准备,是一种日积月累的积淀,是一种精心雕琢的过程．

例6　某城市街道分布如图①,一个居民要从A处前往B处,为了使其所走距离最短,规定只能向右或向下走,那么该居民共有几条可选择的路线?

(“五羊杯”竞赛题)

分析与解　从单个的小正方形思考,寻找行走路线的一般规律．

图②中的小正方形,由A→C共有2种走法,图③中的情形,从A→D共有3种走法,由此得出:到右下角终点的走法等于它所在小正方形从左上角到右下角的走法之和,故依次标出每个小正方形的走法,即可获解．如图④可得该居民共有40条可选择的路线．

例7　平面上有若干个点,其中任意三点都不在同一直线上,将这些点分成三组,并按下面的规则用线段连接:

①在同一组的任意两点都没有线段连接．

②不在同一组的任意两点间一定有线段连接．

(1)若平面上恰好有9个点,且平均分成三组,那么平面上有多少条线段?

(2)若平面上恰好有9个点,且点数分成二、三、四组,那么平面上有多少条线段?

(3)若平面上共有192条线段,那么平面上至少有多少个点?

(“希望杯”邀请赛试题)

解(1)可以连出3×3＋3×3＋3×3＝27条线段;

(2)可以连出2×3＋2×4＋3×4＝26条线段;

(3)设平面上三组点数分别为m,n,p,S＝m＋n＋p,则可以连出mn＋mp＋np＝192条线段．

因S2＝(m＋n＋p)2＝m2＋n2＋p2＋2mn＋2mp＋2np≥mn＋mp＋np＋2mn＋2mp＋2np＝3(mn＋np＋np)＝3×192＝576＝242,故S≥24,S的最小值是24．事实上,当这24个点平分为三组,每组8个点,恰可以连出8×8＋8×8＋8×8＝192条线段．因此,平面上至少有24个点．

舒展思维

如图①,在3×3的方格图案中有多少个正方形?

此问题的精妙之处在于能快速地把我们带入丰富的数学世界,感知数学发现的基本路径:归纳、类比;诱发我们更为深刻地追问与探究．下面从不同的维度提出问题．

解几何计数问题常常需经历以下步骤:

(1)分析几何结构;

(2)依分析的几何结构运用计数方法求出结果．

分析几何结构,即对几何图形观察、分解(对部分图形视而不见)、组合(对图形的整体把握)．

运用枚举法进行列举时,必须注意无一重复、无一遗漏．因此,枚举法常与分类法结合使用,几何计数有以下常见分类方法:

(1)按图形的类型分类;

(2)按图形的大小分类;

(3)选定参照图形分类．

例8　(1)把图①中的3×3情形拓展到n×n的图形中,正方形的总数是多少?长方形的总数又是多少?对于m×n的图形,正方形与长方形的总数又分别是多少?

(2)类似上述问题,如图②,在3×3×3的立体图形中,正方体的总数是多少?长方体的总数又是多少?在n×n×n,l×m×n的图形中,立方体、长方体的总数又分别是多少?

(3)请你提出更一般的问题．

通过对基本图形2×2,3×3中正方形与长方形总数的计数可归纳发现规律．

1．在正方形格纸上有20个点,其分布如图所示,现用4个点作为正方形的4个顶点,这样总共可以组成_________个正方形．

(上海市竞赛题)

(第1题)

(第2题)

(第3题)

2．如图,是由5×5个小正方形组成的网格图,图中有36个格点,以这些格点为顶点的正方形一共有_________个．

(世界数学团体锦标赛试题)

3．如图所示,图中不包含阴影部分的正方形共有_________个．

(青少年国际城市数学邀请赛试题)

4．50条直线将平面分成n部分,若n≤98,则n可以取的值是_________．

(“五羊杯”竞赛题)

5．有长度分别为1,2,…,9的线段各一条,现从中选出若干条线段组成“线段组”,由这一组线段恰好可以拼接成一个正方形,则这样的线段组的组数为_________．

(全国初中数学联赛题)

科学的发展永远始于问题．

通过学习,学会发现问题和提出问题、探索问题和寻求一般规律．

让数学思维更加舒展,从而走向更深层次的发现．

数学是锻炼思维的体操,精湛的思维艺术常借助数学彰显其力量．

6．如图是由一些等腰直角三角形拼成的图形,若一只蚂蚁欲沿着三角形的边从A点爬到C点,规定在爬行的过程中只能向右方、上方或者斜右上方爬行．请问这只蚂蚁总共有_________条不同的爬行路径?

(国际中小学数学能力检测试题)

(第6题)

(第7题)

7．如图所示的图形中一共能数出(　)个长方形(正方形也算作长方形)．

A．64　B．63　C．60　D．48

(“五羊杯”竞赛题)

8．如图,连接边长为1的正方形各边的中点,连正方形的对角线,则图中共有(　)个等腰直角三角形．

A．16　B．32　C．22　D．44

(江西省南昌市竞赛题)

(第8题)

(第9题)

9．如图所示的阴影部分是由方格纸上三个小方格组成,称这样的图案为“L”形,那么,在由4×5个小方格组成的方格纸上可以画出不同位置的“L”形图案(　)个．

A．16　B．32　C．48　D．64

(浙江省竞赛题)

10．边长为整数、周长为20的三角形共有(　)个．

A．4　B．6　C．8　D．12

(江西省南昌市竞赛题)

11．设一个三角形的三边长为正整数a,n,b,其中b≤n≤a,则对于给定的边长n,所有这样的三角形的个数是(　)．

A．n　B．n＋1

C．n2＋n　D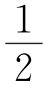．n(n＋1)

(江苏省竞赛题)

12．如图所示,点A1、A2、A3、A4是某市正方形道路网的部分交会点,且它们都位于同一条对角线上．A3处因修路不通,请问某人从点A1出发,不经过A3到达点A4的走法共有多少种?(规定只能向右或向下行走)

A．8　B．10　C．20

D．15　E．12

(第12题)

(美国数学竞赛题)

13．如图,平面上的64个点组成一个8×8点阵,同一行或同一列上相邻的两个点的距离都是1cm．请问以这6个点中的4个点为顶点,而且面积为12cm2的长方形有多少个?

(英国数学竞赛题)

(第13题)

(第14题)

(第16题)

14．在如图所示的5×8方格表中,有两个小方格内标上“”,而图中两个3×4的方格表内部都包含有这两个有记号的小方格．问:共有多少个不同位置的方格表内部包含至少一个有记号的小方格?

(青少年数学国际城市邀请赛试题)

15．在平面上画5条直线l1,l2,l3,l4,l5,使得其中任两条都不平行,任三条都不通过同一点．请你回答:

(1)这5条直线共有多少个交点?在每条直线上恰有几个交点?在这5条直线上共有多少条线段?

(2)以这些线段为边至多可形成多少个等腰三角形?请你简述理由并画出相应的图形．

(北京市竞赛题)

16．如图是由16个面积为1的等边三角形组成的一个大的等边三角形,这个大的等边三角形内部及边上共有15个交点．请回答:

(1)以这些交点为顶点,可以连成多少个等边三角形?

(2)所连成的全部等边三角形的面积的总和是多少?

17．在一个△ABC内部给出m个点,在这些点之间及这些点与A,B,C三点之间连接一些线段,这些线段在三角形内部没有这m个点以外的公共点,并恰将△ABC分成的小区域全部都是小三角形,请你证明:

(1)分成的小三角形区域的总个数必为奇数;

(2)位于三角形内部的所连接线段的条数是3的倍数．

(第17题)

(北京市竞赛题)

例1　24　19　a4＝52－1＝24;a8＝92－1＝80,a9＝102－1＝99,a9＝a8＋19．

例2　D　(1＋2＋3＋4)×(1＋2)×2＋(1＋2)×(1＋2＋3＋4＋5＋6)－(1＋2)×(1＋2)×2＝105．

例3　n条直线最多将圆分成1＋1＋2＋3＋…＋n＝1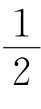＋n(n＋1)块．当n＝62时,1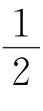＋n(n＋1)＝1954;当n＝63时,1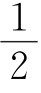＋n(n＋1)＝2017．故至少要画63条直线,可以将圆形纸片分成不少于2003个小纸片．

例4　设三角形另两边长分别为a,b,其中a,b为正整数,且a≤b,则0＜a≤b≤8．

∵a＋b＞8,　∴2b＞8,b＞4,得5≤b≤8,且8－b＜a≤b．

当b＝5时,a＝4,5;

当b＝6时,a＝3,4,5,6;

当b＝7时,a＝2,3,4,5,6,7;

当b＝8时,a＝1,2,3,4,5,6,7,8．

故满足条件的互不全等的三角形共有2＋4＋6＋8＝20(个)．

例8　(1)在n×n的图形中,正方形的总数是12＋22＋…＋n2,长方形的总数是13＋23＋…＋n3,在m×n的图形中,长方形的总数是(1＋2＋…＋m)(1＋2＋…＋n)．

(2)在n×n×n的立方体中,正方体的总数是13＋23＋…＋n3,长方体的总数是(1＋2＋3＋…＋n)3．

(3)如图①,图中有多少个平行四边形?更一般的规律是什么?

如图②,图中有多少个正三角形?更一般的规律是什么?

(例8)

1．21　边长由小到大正方形个数分别为9,4,2,4,2．

2．105　水平放置的正方形有52＋42＋32＋22＋12＝55(个),倾斜放置的正方形有0×52＋1×42＋2×32＋3×22＋4×12＝50(个),共有55＋50＝105(个)．

3．150　不包含阴影部分的正方形有大小不同的几种类型:

面积为1的正方形:9×9－3×3＝81－9＝72;

面积为4的正方形:8×8－4×4＝64－16＝48;

面积为9的正方形:7×7－5×5＝49－25＝24;

面积为16的正方形:6;

共有:72＋48＋24＋6＝150个．

4．98

5．9　正方形边长至少为7,不大于＝11．　7＝1＋6＝2＋5＝3＋4,8＝1＋7＝2＋6＝3＋5,9＝1＋8＝2＋7＝3＋6＝4＋5,10＝1＋9＝2＋8＝3＋7＝4＋6,11＝2＋9＝3＋8＝4＋7＝5＋6．组成边长为7,8,10,11的正方形各有一种方法;组成边长为9的正方形有五种方法．

6．42　如图,图中各点的数即为蚂蚁从起点到该点的不同路径数．

7．B

8．D　斜边长分别为的等腰直角三角形个数分别为4,16,8,16,共有4＋16＋8＋16＝44个等腰直角三角形．

9．C　每个2×2小方格中“L”形图案有4种不同画法,而位置不同的2×2小方格有12个,故共有12×4＝48个“L”形图案．

10．C　设三角形三边长为a,b,c(a≥b≥c),由a＋b＋c＝20又a＋b＞a,得7≤a≤19,可列出(a,b,c)＝(9,9,2),(9,8,3),(9,7,4),(9,6,5),(8,8,4),(8,7,5),(8,6,6),(7,7,6)．

11．D　见表．

(第6题)

故符合条件的所有三角形共有1＋2＋3＋…＋n＝(个)．

12．A　如图,每一点旁的数代表从A1走到该点的走法数．

13．连接同一行和同一列的点可构成一个网格．首先考虑边平行于网格线的长方形．对于形状为2×6的长方形,它的方向有2种选择(水平和铅直),其中一组对边有8－6＝2种选择,另外一组对边有8－2＝6种选择,所以这样的长方形一共有2×2×6＝24个．对于形状为3×4的长方形,它的方向也有2种选择,其中一组对边有8－4＝4种选择,另外一组对边有8－3＝5种选择,所以这样的长方形一共有2×4×5＝40个．除了这些长方形,还有边平行于网格的对角线的长方形,它们形状分别为和

(第12题)

这2种长方形也分别有2种方向可选择,首先考虑长方形的最长边从左下方伸到右上方的这个方向．第一种形状的长方形只有1个,如图所示;第二种形状的长方形有9个,其中一个已在图中标出．这9个长方形的左上角的顶点已在图中用黑点标出．所以这2种形状的长方形一共有2×(1＋9)＝20个．因为12＝22×3,而3不能表示为2个完全平方数的和,所以再也没有其他形状的长方形．因此要求的长方形一共有24＋40＋20＝84个．

(第13题)

14．对于包含左边记号小方格的方格表,其左边所在直线有四种选择,右边所在直线有五种选择,上边所在直线有两种选择,下边所在直线有四种选择．故这样的方格表总共有4×5×2×4＝160(种)．

同理,对于包含右边记号小方格的方格表,总共有6×3×3×3＝162(种);对于同时包含两个记号小方格的方格表,总共有4×3×2×3＝72(种)．

因此,包含至少一个记号小方格的方格表总数为160＋162－72＝250(种)．

15．(1)如图①,满足题设条件的5条直线共有10个交点;在每条直线上恰有4个交点;由于在每条直线上有6条线段,因此在这5条直线上共有30条线段．

(2)能够形成以这些线段为边的等腰三角形最多有10个．理由如下:

记la与lb的交点为Aab,我们考察底边在l1上的等腰三角形,l1上有4个交点A1k,k＝2,3,4,5,若底边为A12A13,则∠A23A12A13＝∠A23A13A12是锐角．

此时,线段A12A14不能再为某个等腰三角形的底边;否则,会出现l3∥l4或l2∥l4,与题设条件矛盾．类似的,A12A15,A13A14,A13A15均不能再为某个等腰三角形的底边．

又在A12A13为底边的情况下,A14A15也可以为等腰三角形的底边,于是,在每条直线上至多有两个等腰三角形的底边,它们是以两个端点均不同的两条线段为等腰三角形底边的．从而,在这五条直线上以形成的线段为底边的等腰三角形的个数至多为2×5＝10．

(第15题)

事实上,这样的10个等腰三角形的构图是存在的．

如图②的正五角形．

16．(1)面积是1的等边三角形,有16个,面积是4的等边三角形有7个,面积是9的等边三角形有3个,面积是16的等边三角形有1个．此外,面积是3的等边三角形有6个,面积是7的等边三角形有2个．故可以连成的等边三角形共有:16＋7＋3＋1＋6＋2＝35(个)．

(2)所连成的全部等边三角形面积的总和为:1×16＋4×7＋9×3＋16×1＋3×6＋7×2＝119．

17．(1)设小三角形的总数为n,这n个小三角形的边中有3条是原三角形的边AB,BC,CA,所以位于内部的小三角形的边数(位于三角形内部的所连线段的条数)为3n－3,而且这些边每一条属于两个小三角形．设e为位于△ABC内部的边的数目,则2e＝3n－3＝3(n－1),于是有3(n－1)是偶数,n－1是偶数,所以,分成的小三角形的数目n必为奇数个．

(2)显然3|2e,而(3,2)＝1,∴3|e．即位于三角形内部的所连线段的条数是3的倍数．