若r=1,则λ1=…......
2023-11-21
用一种多边形或几种多边形组合的平面镶嵌,都是按一定规则重复而铺镶,这种镶嵌称为匀称周期性镶嵌.英国数学家彭罗斯发现了只用两块拼板就能进行平面的非周期性镶嵌,这种拼板的一组是由两个角度不同的菱形组成,分别为72°,108°和36°,144°.
知能概述
在生活生产实践和科学研究中,我们既需进行严谨细致的精确计算,又常要对一些问题的数量进行估算,估算能让我们对所考察的事物迅即有一个全局的理解和把握,是我们研究和处理有关数量问题时经常运用的一种方法.
估算不是漫无目标的胡估乱算,必须仔细审题,充分理解题意,调动经验、知识、直觉,并常用到放缩、夹逼、排序等方法.
问题解决
例1 100名少年运动员胸前的号码分别是1,2,3,…,99,100,选出其中的k名运动员,使得它们的号码数之和等于2008,那么k的最大值是_________.
(少年数学精英邀请赛试题)
解题思路 选号码越小的,可以使选出的人数越多,故考虑选由1~n的连续n个自然数之和不超过2008的k的值.
纯粹数学与应用数学是理解世界及其发展的一把主要钥匙.
——联合国教科文组织
费米难题
费米,当代美国著名物理学家,因崇高的人格、优秀的品质而具有迷人的科学风采,1938年获诺贝尔物理学奖.
有一次费米问学生们芝加哥市一共有多少位钢琴调音师,见学生们茫然,费米提示把这个问题“分解成一些便于操作的小问题,然后鼓起勇气作猜测和假设”.
例2 如果自然数a,b,c满足29a+30b+31c=366,则a+b+c=( ).
A.10 B.12 C.14 D.16
(江苏省竞赛题)
解题思路 题设条件是三元不定方程,适当改变字母系数,放大或缩小求出a+b+c的取值范围.
例4 求![]() 中的数字x,y,z.
中的数字x,y,z.
(全俄中学生数学竞赛题)
解题思路 从估算![]() 值的大小,建立关于x的不等式组入手.通过夹逼,把多元问题转化为解一元一次不等式,逼近求解.
值的大小,建立关于x的不等式组入手.通过夹逼,把多元问题转化为解一元一次不等式,逼近求解.
所谓放缩法,就是将问题中的某些量放大或缩小,使各量之间的关系清晰地显现出来,是处理等式、不等式问题的一种重要方法.
所谓夹逼法,就是把问题的解限制在某取值范围内,通过解不等式、筛选讨论,得到问题的解.
例5 给出四个自然数a,b,c,d,其中每三个数之和分别是180,197,208,222,求a,b,c,d中最大的数的值.
(“希望杯”邀请赛试题)
解题思路 一般的解法是解关于a,b,c,d的四元一次方程组,由题意知a,b,c,d互不相等,不妨设a<b<c<d,思维定向,可优化解题过程.
例6 当x≤y≤z时,求方程![]() 的正整数解.
的正整数解.
(山西省太原市竞赛题)
排序
在解一些涉及多个变元的数学问题时,题设条件并没有给出变元的大小顺序,若给它们假设一个大小顺序,并不影响命题的成立,则给问题的解决增加了一个可供使用的条件,从而降低问题的难度,这种方法叫排序法.
例7 如果正整数x1,x2,x3,x4,x5满足x1+x2+x3+x4+x5=x1x2x3x4x5,求x5的最大值.
有序是系统的基本属性,是维持系统的重要条件.
相等与不等是矛盾的两方面.在一定条件下可以相互转化.
例6是利用不等关系研究相等关系的典型例题,通过排序与放缩,将多元不定方程转化为一元不等式,逼近求解.
数学家如何思考?他们的想法怎样与外部世界发生联系?数学是最纯粹的思想形式,其中外部世界几乎被隔离出去了.
解 因xi的地位轮换对称,故x5的最大值也就是x1,x2,x3,x4,x5中的最大值.为确定起见,不妨设x1≤x2≤x3≤x4≤x5(排序),则
于是得x4x5-x4-x5≤3,即(x4-1)(x5-1)≤4.
若x4=1,则x1=x2=x3=x4=1,与题设等式为4+x5=x5矛盾;
若x4>1,则x5-1≤4,即x5≤5.
当x5=5时,容易找到满足条件的数组(1,1,1,2,5),所以x5的最大值是5.
1.若实数a≥b≥c≥d≥0,且a+b+c+d=100,则b的最大值是_________,b+c的最大值是_________.
(“希望杯”邀请赛试题)
2.将2,3,4,5,…,10,11这10个自然数填到图中10个格子里,每个格子只填一个数,使得“田”字形的4个格子中所填数字之和都等于P,那么P的最大值是________.
(第2题)
(江苏省竞赛题)
3.设x1,x2,x3,x4,x5是正整数,任取其中四个求和后得到的结果是44,45,46,47,则这五个正整数分别是_________.
(清华大学自主招生试题)
4.有n个连续的自然数1,2,…,n,去掉其中的一个数x后,剩下的数的平均数是16,则满足条件的n和x的值分别是_________.
(天津市竞赛题)
5.如果一个两位数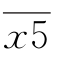 与一个三位数
与一个三位数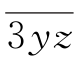 的积为29400,那么x+y+z=_________.
的积为29400,那么x+y+z=_________.
(上海市竞赛题)
6.已知长方体的长、宽、高都是整数厘米,将长、宽、高都增加1厘米,长方体的表面积可能增加( )平方厘米.
A.14 B.103 C.214 D.400
(“希望杯”邀请赛试题)
7.一个凸n边形,它的每个内角的度数都是整数,且任意两个内角的度数都不相同,则n的最大值是( ).
A.6 B.12 C.26 D.93 E.179
(美国数学竞赛题)
下面这个式子叫“反平方级数”:
数学家贝努利曾求出过许多级数的和,但对于上述问题却束手无策,曾向欧拉求教,欧拉用类比的方法求出这个级数的和为 .这个故事成为数学史上的一段佳话.
.这个故事成为数学史上的一段佳话.
请你估计一下,这个级数的前100项之和是否满足不等式:
8.在冬季篮球赛中,选手小明在第六、第七、第八、第九场比赛中分别得了23分、14分、11分和20分.他的前九场的平均成绩高于前五场的平均成绩,如果他的前十场的平均成绩高于18分,那么他的第十场的成绩至少为( ).
A.27分 B.29分 C.31分 D.33分
(广西壮族自治区竞赛题)
9.设正整数n可以等于4个不同的正整数的倒数之和,则这样的n的个数是( ).
A.1 B.2 C.3 D.4
(复旦大学自主招生试题)
10.x1,x2,…,x100是自然数,且x1<x2<…<x100,若x1+x2+…+x100=7001,那么,x1+x2+…+x10的最大值为( ).
A.2225 B.2226 C.2227 D.2228
(“希望杯”邀请赛试题)
11.已知由小到大的10个正整数a1,a2,a3,…,a10的和是2000,求a5的最大值.
(江苏省竞赛题)
12.设x,y,z为互不相等的正整数,且![]() =a,a为整数,求x,y,z的正整数解.
=a,a为整数,求x,y,z的正整数解.
(河南省竞赛题)
13.有5个数,每两个数的和分别为2,3,4,5,6,7,8,6,5,4(未按顺序排列),求这5个数的值.
(江苏省竞赛题)
14.一个三位数,将它的三个数字两两相乘、三个数字的乘积相加,其和恰好等于它本身,这样的三位数中最小的是多少?
(“华罗庚金杯”少年数学邀请赛试题)
15.设a1,a2,a3,…,an是各不相同的正自然数,a≥2,求证:![]()
![]()
(中国科学技术大学自主招生试题)
16.有位学生忘记写两个三位数间的乘号,得到一个六位数,这个六位数恰好为原来两个三位数的乘积的3倍,这个六位数是多少?
(全国初中数学联赛试题)
17.1995年以前,乌克兰足球锦标赛的计分规则为每支球队获胜得2分,打平得1分,输球得0分;从1995年开始,足球联盟决定将原来的计分规则改为:每支球队获胜得3分,打平得1分,输球得0分,并相信这样的改变不会大范围影响排名的分布情形.然而,在1927年的一届n支球队参加的锦标赛中,每支球队均要与其他球队恰比一场,最终A队获得总分最高,B队获得最低分;但若使用新规则,B队将获得最高分而A队获得最低分.求这各情形发生时n的最小值.
注:这里的“最高(低)分”指的是唯一的最高(低)分.
(乌克兰数学竞赛题)
例1 62 由1+2+3…+n=![]() <2008,得n(n+1)≤4016.
<2008,得n(n+1)≤4016.
∵60×60=3600,70×70=4900,故n是两位数,其十位数字是6,试算62×63=3906<4016,63×64=4032>4016,于是取n=62,即最多能选出62人.
例5 最大数为89.
1.50 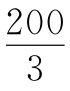 由2b≤a+b+c+d=100,得b≤50,当a=b=50,c=d=0时,等号成立.又a≤a+d=100-(b+c),2a≥b+c,a≥
由2b≤a+b+c+d=100,得b≤50,当a=b=50,c=d=0时,等号成立.又a≤a+d=100-(b+c),2a≥b+c,a≥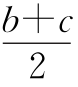 ,100-(b+c)≥
,100-(b+c)≥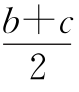 ,得b+c≤
,得b+c≤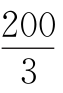 ,当a=b=c=
,当a=b=c=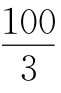 ,d=0时满足要求.
,d=0时满足要求.
2.28 设居中两个格子所填之数为x,y,则2+3+4+…+10+11+x+y=65+x+y=3P.要使P最大,必须x+y最大,由于x+y≤10+11=21,得3P≤65+21=86.解得P≤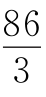 =28
=28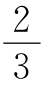 ,所以P取得最大整数值应为28.
,所以P取得最大整数值应为28.
(第2题)
3.10,11,11,12,13
226=44+44+45+46+47≤4(x1+x2+x3+x4+x5)≤44+45+46+47+47=229,x1+x2+x3+x4+x5=57.
6.C 设长方体的长、宽、高分别为acm,bcm,ccm,则长方体的表面积增加:2[(a+1)(b+1)+(b+1)(c+1)+(a+1)(c+1)]-2(ab+bc+ac)=4(a+b+c)+6,
∵4(a+b+c)+6≥4(1+1+1)+6=18,题设的选项中,只有214可表示成4×52+6的形式.∴选C.
7.C 要使n最大,只需让每个外角的度数尽可能小,可令外角分别是1°,2°,3°…,因1+2+3+…+26=351<360,1+2+3+…+27=378>360,故nmax=26.26个外角分别为1°,2°,3°…25°,35°,此时多边形的内角分别为179°,178°,177°,…,155°,145°.
10.B 7001=x1+x2+…+x100≥x1+(x1+1)+(x1+2)+…+(x1+99),解得x1≤20,又20+21+22+…+119=6950=7001-51,21+22+…+120=7050>7001,故当x1=20,x2=21,…,x49=68,x50=70,x51=71,…,x100=120时,x1+x2+…+x50有最大值,最大值为2226.
11.要使a5最大,需使a1,a2,a3,a4及a6,…,a10尽量小,又因a1<a2<…<a10,故先取a1,a2,a3,a4分别为1,2,3,4,于是有2000=1+2+3+4+a5+…+a10,即a5+a6+…+a10=1990.又a6≥a5+1,a7≥a5+2,a8≥a5+3,a9≥a5+4,a10≥a5+5,故a5+a6+…+a10≥6a5+15,即6a5≤1975,![]() ,故a5最大值可取329.
,故a5最大值可取329.
12.设x<y<z,则x≥1,y≥2,z≥3.所以![]() ,0<a≤1
,0<a≤1 ,得a=1.解方程
,得a=1.解方程![]() ,得(x,y,z)=(2,3,6),(2,6,3),(3,6,2),(3,2,6),(6,2,3),(6,3,2).
,得(x,y,z)=(2,3,6),(2,6,3),(3,6,2),(3,2,6),(6,2,3),(6,3,2).
13.设五个数为a≤b≤c≤d≤e,将和数从小到大重新排列为2,3,4,4,5,5,6,6,7,8,则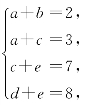
又a+b+c+d+e= (2+3+4+4+5+5+6+6+7+8)=12.5,
(2+3+4+4+5+5+6+6+7+8)=12.5,
进而可求得d=3.5,e=4.5,c=2.5,a=0.5,b=1.5.
14.设这个三位数为![]() ,则100a+10b+c=a+b+c+ab+bc+ca+abc,得c=
,则100a+10b+c=a+b+c+ab+bc+ca+abc,得c=![]() ,因c≤9,故99a+9b-ab≤9a+9b+9ab,得b=9,c=9,从而知这样的三位数中最小的数是199.
,因c≤9,故99a+9b-ab≤9a+9b+9ab,得b=9,c=9,从而知这样的三位数中最小的数是199.
15.设a1<a2<a3<…<an,则有ai≥i(i=1,2,3,…,n).
16.设两个三位数分别为x和y,由题设知 1000x+y=3xy. ①
由①式得y=3xy-1000x=(3y-1000)x,故y是x的整数倍,不妨设y=tx(t为正整数),代入①式得1000+t=3tx,所以x=![]() .因为是三位数,所以x=
.因为是三位数,所以x=![]() ≥100,从而可得t≤
≥100,从而可得t≤![]() ,又t为正整数,故t的可能的取值只能是1,2,3.
,又t为正整数,故t的可能的取值只能是1,2,3.
验证可知:只有t=2符合题意,所以t=2,x=167,y=334,所求的六位数为167334.
17.由题意,假设A队赢了x场,平了y场,B队赢了a场,平了b场,显然不止两支球队,其他球队的得分均介于A、B两队之间.
则![]()
⇒2(a-x)+2≤y-b≤3(a-x)-2⇒a-x≥4⇒y-b≥10⇒y≥10+b⇒y≥10.
而x≥1,从而,x+y≥11.
因此,至少有12支球队,n≥12.
下表构造说明n=12可以取到.
有关精英数学大视野·七年级2020的文章

由此就可求得设计流域年枯水流量的统计参数,从而近似估算出设计枯水流量。同时,还需通过野外查勘,观测设计站的枯水流量,并与参证站同时实测的枯水流量进行对比,以便合理确定设计站的设计枯水流量。......
2023-06-21

猪腰中含有丰富的钙、磷、铁等矿物质和维生素等,能够帮助人体补充维生素。食用猪腰,可以起到补肾气、通膀胱、消积滞、止消渴的作用。另外,食用猪腰时,应该避免与茄子搭配同食。储存猪腰时,最好用保鲜膜包裹好置于冰箱内冷藏,但是也应尽快食用。做法:剖开猪腰,去除白筋,用清水浸泡30分钟。......
2023-11-29

“解决问题”研究所谓应用题,就是“从实际生活中提取出来,让学生运用所学的数学知识来解决问题的习题。”但在《标准》颁布之后,“解决问题”的教学已成为小学数学教学的一个主要任务,而培养学生在模拟的现实情境中提出问题、分析问题、解决问题的能力是小学数学新课程标准的一个基本要求,也是小学数学教学的一个主要目标。为了解决这个难题,曾家岩小学在2010年申报了“小学数学解决问题的研究与实践”课题。......
2023-08-31

通常用于环境和能源政策实证研究的模型包括四类:项目级模型、局部均衡模型、可计算一般均衡模型以及集成评价模型。本文研究中采用的中国CGE模型是由国务院发展研究中心开发的DRC-CGE模型的2007版,DRCCGE2007包括42个生产部门和分城乡的14类居民家庭[3],以及五种初级生产要素,即农用土地、资本、农业劳动力、非熟练劳动力和专业劳动力[4]。......
2023-07-03

图4.35旋转头这种方法将机器上料的前后操作时间减少到最低限度,因为旋转可以在没有任何移动或操作装置很少移动的情况下运行。图4.42集成电路的旋转模块这些模块通过附加轴进行扩展,允许简单旋转的附加运动自由度。图4.43适用于不同应用的电动旋转变位模块机械手或工具旋转有关的一个主要问题是上料。......
2023-06-15

+n3.解题思路问题的解决为其他问题的解决提供帮助,而其解决的常用方法有:拆项相消、倒序相加、数形结合等.拆项相消具有一般性,需要突破分数拆项的思维定式,如n(n+1)].1.计算:“数学王子”高斯从小就善于观察和思考,在他读小学时就能在课堂上快速地计算出1+2+3+…......
2023-08-13

价钱、时间、质量、长度、面积、体积等在日常生活中可谓是随处可见、随时可遇、随地可用。经验之于教育、之于学习、之于学生成长的重要性是显然的。《课标》中,认识元、角、分的内容中提出“了解它们之间关系”的要求;认识年、月、日中也提出“了解它们之间关系”的要求。当然,这里提的解决实际问题的能力,不只是指解决问题的能力,也包括发现问题、提出问题、分析问题的能力,也就是《课标》中提出的“四能”。......
2023-08-11
相关推荐