数学大视野·七年级2020：第26讲，抽象与具体，分析与解题

上图是在世界数学光效应艺术绘画作品展中展出的,其构成方式是:假设在正多边形每个顶点处各有一只小狗,它们互相追逐,便构成了等角螺线的组合图形．

知能概述

苏联著名数学家柯尔莫哥洛夫在《数学:它的内容、方法和意义》一书中指出数学有三大特点,即抽象性、严谨性、应用的广泛性．

抽象,即从具体事物中抽取出来的相对独立的属性、关系等．数学抽象舍弃事物的一切方面而仅保留数量关系和空间形式．

数学是抽象的,但又是具体的．

抽象的数学来源于具体的例子,若能掌握丰富的具体例子,则能更好地理解数学,否则,抽象就变为无源之水,无本之木．

抽象与具体的关系在解决问题过程中体现于:

(1)从具体到抽象,更深刻地揭示问题的一般性;

(2)由抽象到具体,更清晰地呈现问题的特殊性．

问题解决

例1　已知x无论取什么值,式子必为同一定值,那么的值为_________．

(“华罗庚金杯”香港中学邀请赛试题)

解题思路　对x取特殊值,呈现定值,并求出a,b的关系．

一位好的数学家与一个蹩脚的数学家之间的差别,在于前者手中有很多具体的例子,而后者只有抽象的理论．

——陈省身

西班牙著名画家毕加索在画《公牛》时,数易其稿,从具体到抽象,从复杂到简单,笔简意赅,形似神更似．

例2　自然数a,b,c,d满足＝1,则＋＝(　)．

(北京市竞赛题)

解题思路　找出满足条件等式的a,b,c,d的具体值．

例3　设,求A的整数部分．

(北京市竞赛题)

解题思路　从揭示A中第n项的特征入手．

例4　有这样的两位数,交换该数数码所得到的两位数与原数的和是一个完全平方数．例如:29就是这样的两位数,因为29＋92＝121＝112,请你找出所有这样的两位数．

(江苏省竞赛题)

解题思路　设原数为,则新数为,发现的特点是解本例的关键．

由抽象到具体基本方法有:

(1)以退求进,考虑简单情形、特殊情形．

(2)恰当赋值,即在条件允许的范围内赋予字母以特殊值来计算、判断或探求解题思路．

由具体到抽象,常反映在用字母表示数,有利于揭示问题中的数量关系,便于找到数量的相依关系或相等不等关系．

例5　(1)桌面上有七只杯子,其中三只杯口朝上、四只杯口朝下,每人每次翻转四只杯子．问经过若干人翻动后,能否使这七只杯子杯口全部朝下?

(2)在操场上有101名学生面向南站成一排,每次口令使其中任意10名学生向后转,称为一次“反向运动”．证明:无论经过多少次“反向运动”,都不可能使得所有学生都同时面向北．

分析与解　电灯的亮与灭,开关的开与关,朝南与朝北,向上与向下……两态情形是现实世界中最简单最基本的运算状态,这类具有两态的量都有相反的意义,自然想到运用数学中的正数、负数来描述．我们用＋1与－1表示两态,以(－1)n表示这两态之间改变状态的n次操作,也就是将两态变化问题抽象为(－1)n的数学模型．

下面对(1)给出解答:

杯口朝上状态记为＋1,杯口朝下状态记为－1．

初始状态:标志量为(＋1)3×(－1)4＝＋1,

最终状态:标志量为(－1)7＝－1．

每次翻动4只杯子的操作相当于乘以(－1)4,n个人翻转的操作,相当于乘以

于是由初始状态经过n个人翻转变为[(＋1)3×(－1)4]×(－1)4n＝＋1．

无论n为何值,都不可能变为标志量－1,故永远不能按题设的操作使七只杯子杯口全部朝下．

(2)同理．

例6　华罗庚教授在一首诗文中勉励青少年:“猛攻苦战是第一,熟练生出百巧来．勤能补拙是良训,一分辛劳一分才．”现在将诗文中不同的汉字对应不同的自然数,相同的汉字对应相同的自然数,结果不同汉字所对应的自然数可以排列成一串连续的自然数．如果这28个自然数的平均值是23,问“分”字对应的自然数的最大可能值是多少?

(“华罗庚金杯”少年数学邀请赛试题)

分析与解　题中28个字,“分”出现2次,“是”出现2次,“一”出现3次,其他字均各出现一次．

28个自然数的平均数是23,其中有24个是连续的自然数．

先想一个由二十多个连续自然数组成,并且平均数是23的具体例子．

25个连续自然数　11,12,13,…,35　①的平均数就是23．①是由23开始,向左、向右各写12个数得到的,24个连续自然数的平均数不能是23．

因为只有24个不同的字,我们去掉①中最小的11(剩下的24个仍是连续的自然数),增加1个13、1个35．这样,总和比23×26多出(13－11)＋(35－23)＝14．

如果再增加两个16(16＝23－14÷2),那么28个数的平均数正好是23．

所以出现2次的“分”可以是35．

“分”能不能再大一些呢?

例5表明,许多不同的实例,经过抽象却有共同的本质,领悟不同问题的共同本质,就能对“形异而质同”的问题迅速识别,并提取相应的方法加以解决．

具体的例子可以帮助我们猜想结论,可以引出命题的证明．

解题还应学会将抽象问题具体化．

老子说:“天下难事,必作于易;天下大事,必作于细。”从简单的情形做起,是最基本的数学素养．

不能了．如果“分”≥36,那么这28个数的和至少是

13＋14＋…＋36＋36＋13＋13＋14

＝23×28＋(36－11)＋(36－12)－(23－13)－(23－13)－(23－14)

＝23×28＋20,

它们的平均数大于23,因此“分”最大是35．

数学的眼光

数学的眼光是观察世界的一种视角、认识世界的一种方式．精确的量化与严格的证明是数学区别于其他学科最显著的特点,抽象、化归、建模、推理是数学的基本思想．

数学的眼光是探寻的、洞察的、深邃的、辩证的．在复杂的表象中去发现数的规律,去寻找形的结构．

例7　甜饮料里有糖的质量分数,那么,给糖水添上一点糖,糖水就更甜了．请你把这一生活常识用数学式子表达出来．

分析与解　从生活常识到“数学不等式”历经以下三个步骤:

(1)用字母a,b,m表示相应的量;

(2)根据质量分数的定义,写出加糖前后的质量分数;

(3)将“更甜了”表示为不等式,其中b＞a＞0,m＞0．

进一步追问:

(1)怎样证明上述不等式?

(2)将一个分数的分子、分母同时加上一个正数,这个分数变大了吗?

数学是常识的精微化．荷兰著名数学家弗赖登塔尔说:“与其说教数学,不如说教数学化．”

例7是一个数学化的探究过程．我们不能说“糖水加糖更甜了”是数学,但提炼为真分数不等式就是数学了．

1．把(x2－x＋1)6展开后得a12x12＋a11x11＋…＋a2x2＋a1x＋a0,则a12＋a10＋a8＋a6＋a4＋a2＋a0＝_________．

(“祖冲之杯”邀请赛试题)

2．当a取符合na＋3≠0的任意数时,式子的值都是一个定值,其中m－n＝6,那么m＝_________,n＝_________．

(北京市“迎春杯”竞赛题)

3．在图中有8个顶点,每个顶点处各有一个数,每个顶点处的数正好等于3个相邻顶点(有线段相连的两个顶点称为相邻顶点)处的数的平均数,则a＋b＋c＋d－(e＋f＋g＋h)＝_________．

(第3题)

(“希望杯”邀请赛试题)

4．从十个英文字母A,B,C,D,E,F,G,X,Y,Z中任选五个字母(字母允许重复)组成一个“词”,将所有可能的“词”按“字典次序”(即英汉辞典中英语词汇排列的顺序)排列,得到一个“词表”:AAAAA,AAAAB,AAAAC,…AAAAZ,AAABA,AAABB,…,DEGXY,DEGXZ,DEGYA,…,ZZZZY,ZZZZZ,设位于词CYZGB与词XEFDA之间(这两个词本身除外)的词的个数是k,则k＝_________,“词表”中的第k个词是_________．

(“五羊杯”竞赛题)

5．现有一列数a1,a2,…,a100,其中a3＝9,a7＝－7,a98＝－1,且满足任意相邻三个数的和为同一常数,则a1＋a2＋…＋a100的值为(　)．

A．0　B．40　C．32　D．26

(湖北省武汉市竞赛题)

6．在黑板上按下面的方案写出数:第一行写数1;在第二行写两个数2和3;在第三行写3个数3,4和5;以此类推(在第n行写由n开始的n个连续的自然数)．一直写到2000行,这时在黑板上写出2018共有(　)次．

A．991　B．993　C．995　D．997　E．999

(国际中小学数学能力检测题)

7．设S是平面上的一个凹六边形,且它的任意3个顶点都不共线,称一个以S的某些顶点为顶点的多边形为一个S多边形,则下面的结果一定不正确的是(　)．

A．每个S四边形都是凸四边形

B．存在S五边形为凸五边形

C．每个S五边形都不是凸五边形

D．至少有两个S四边形是凸四边形

(复旦大学自主招生试题)

8．从长度分别是1,2,3,…,14的14条线段中任取出n条,其中必有3条线段能构成一个三角形,则n的最小值是(　)．

A．7　B．8　C．9　D．10

(“希望杯”邀请赛试题)

9．计算

(广西壮族自治区竞赛题)

(江苏省竞赛题)

10．已知a－b＝7,且ax＋2≠0,若不论x取何值,代数式的值都相等,求a,b的值．

(浙江省湖州市竞赛题)

11．有一张纸,第1次把它分割成4片,第2次把其中的1片分割成4片,以后每一次都把前面所得的其中一片分割成4片,如此进行下去,试问:

(1)经5次分割后,共得到多少张纸片?

(2)经n次分割后,共得到多少张纸片?

(3)能否经若干次分割后共得到2003张纸片?为什么?

(江苏省竞赛题)

12．有位学生漫不经心地作了下列错误的“约分”:闹出了大笑话,令人惊讶的是,约分虽然不合法,但结果却是对的．请找出分子、分母都是两位数且符合上述约分的真分数．

(摘自马克士威尔《数学中的谬误》)

13．17×17枚硬币按正方形摆放．起初,所有硬币都是正面朝上的,每一次翻转五枚相邻的(或水平或垂直或对角)硬币．如此有限多次翻转后,所有的硬币有无可能都是背面朝上?

(日本数学奥林匹克试题)

14．NBA常规赛有30支球队参加．问:可否将30支球队分为东部、西部两个联盟,及适当指定任意两队间比赛的场数,使得每支球队均恰参加了82场比赛且东部球队和西部球队之间比赛的场数恰是总比赛场数的一半?

(俄罗斯数学竞赛题)

15．若a1,a2,…,an均为正整数,且a1＜a2＜…＜an≤2007．为保证这些整数中总存在四个互不相同的数ai,aj,ak,al,使得ai＋aj＝ak＋al＝an,那么,n的最小值是多少?请说明理由．

(山东省竞赛题)

16．求所有正整数n,使得存在正整数x1,x2,…,x2012满足x1＜x2＜…＜x2012,且

(《数学周报》杯全国初中数学竞赛题)

17．圆周上标有40个红点、30个蓝点、20个绿点,圆周被分割成90段弧,每段弧依两端点的颜色写上一个数:红—蓝弧写1,红—绿弧写2,蓝—绿弧写3,两端点同色的弧写0．求所有数之和的最小值和最大值．

(全国初中数学竞赛题)

例4　(10a＋b)＋(10b＋a)＝11(a＋b),因而a＋b是11的倍数,则a＋b＝11·k,且k是完全平方数,由于a≤b,b≤9,得a＋b≤18,k＝1,从而a＋b＝11．推得这样的两位数有8个:29,38,47,56,65,74,83,92．

1．365　令x＝1,得a12＋a11＋…＋a2＋a1＋a0＝1,　①

令x＝－1,得a12－a11＋…＋a2－a1＋a0＝729,　②

①＋②,得2(a12＋a10＋…＋a2＋a0)＝730,即a12＋a10＋…＋a2＋a0＝365．

2．取a＝0,则,取a＝1,则,又m－n＝6,解得

3．0　符合题设条件的最简单的例子是取a＝b＝c＝d＝e＝f＝g＝h,原式＝0．

4．45568　EFFGX　将十个英文字母A,B,C,D,E,F,G,X,Y,Z,依次对应十个数字0,1,2,3,4,5,6,7,8,9,则每一个“词”对应一个“五位数”,例如:AAAAA对应00000,AAABC对应00012,这样,“词表”可改写为“五位数表”:00000,00001,00002,…,00009,00010,…,99999．

因为CYZGB对应28961,XEFDA对应74530,所以,这两个词之间的词的个数,等于五位数28961与74530之间的五位数的个数,即k＝74530－28961－1＝45568．

注意到00000是数表中的第一个数,故数表中的第k个“五位数”是45568－1＝45567,它对应“词表”中的第k个词就是EFFGX．

5．D　a1＝a4＝a7＝…＝a100＝－7,a2＝a5＝a8＝…＝a98＝－1,a3＝a6＝a9＝…＝a99＝9,原式＝33(9－7－1)－7＝26．

6．A　第n行最后一个数等于2n－1．所以由等式2n－1＝2017,n＝1009得出,在第1010行的数是从1010～2019,倒数第二个数是我们第一次遇到数2018．从1010行到2018行每行遇到数2018一次,这样一来将遇到2000－1010＋1＝991(次)．

7．A　如图①,A1A2A5A6这个四边形就不是凸的,故选项A不正确;如图②,A1A2A3A4A6是凸五边形,故B正确;又A1A2A3A4及A1A4A5A6都是凸四边形,故D也正确;如图③,选项C正确．

(第7题)

8．A　从极端情况思考,先估计n的下界,取长度为1,2,3,5,8,13,共6条线段,其中任意三条都不能作为同一个三角形的三边,n＞6．

9．(1)设,则a－b＝1,

(2)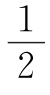　设20012000＝a．

10．a＝2,b＝－5．

11．(1)因为每分割1次,就要增加3张纸片,所以经5次分割,共得到1＋3×5＝16张纸片．

(2)经n次分割,共得到(1＋3n)张纸片．

(3)若能分割得到2003张纸片,则1＋3n＝2003,3n＝2002,无整数解,所以不可能经若干次分割后得到2003张纸片．

12．设这样的真分数为(x,y,a都是一位正整数)．

“非法约分”意味着下式成立:,解得, 讨论得(x,y,a)＝(1,4,6),(2,5,6),(1,5,9),(4,8,9),从而可求得这样的真分数为

13．不可能　如下标识每枚硬币:

则(1)每一次翻转的五枚硬币分别标识为A,B,C,D,E．

(2)同时,对于每个标识A,B,D,E有58枚硬币．而对于C有57枚硬币．

(3)若最后所有的硬币是背面朝上的,则每枚硬币必进行了奇数次翻转．

从(2)和(3)知,标识A的硬币共被翻转偶数次,而标识C的硬币共被翻转奇数次．所以,翻转标识A的硬币的次数不同于翻转标识C的硬币的次数．此与(1)矛盾．因此知是不可能的．

14．不可以．

令x、y、z分别表示东部球队之间、西部球队之间、东部球队与西部球队之间比赛的场数,k为东部球队的队数．则

故82k－2x＝z＝＝15×41,矛盾．

15．取a1＝1,a2＝3,…,a1003＝2005,a1004＝2007,共1004个奇数．显然,其中任何两数之和不等于2007．

若在上述1004个数中再加入数2006,即a1＝1,a2＝3,…,a1003＝2005,a1004＝2006,a1005＝2007,此时,只存在唯一的一对数a1＝1,a1004＝2006,其和为a1005＝2007．

所以,n的最小值不小于1006．

接下来证明:当n≥1006时,一定存在满足条件的四个数．

当an＝2007时,因为2007＝1＋2006＝2＋2005＝…＝1003＋1004,

这表明2007只能分解为1003个不同的两个正整数的和式,所以,当n≥1006,即n－1≥1005时,在除了an＝2007之外的不少于1005个数a1,a2,…,an－1中,至少包含了2007的上述1003个不同分解和式中的两个和式ai＋aj,ak＋al的全部四个加数ai,aj,ak,al,此即题设要求的四个正整数．

当an＜2007时,若an＝2m－1,则an可表示为m个两个不同正整数之和的不同和式;若an＝2m,则an可表示为m－1个两个不同正整数之和的不同和式．an＜2007,所以,m≤1003．除去an之外,在a1,a2,…,an－1这不少于1005个数中至少包含了不超过1003个不同和式中的两个的全部四个加数,此即题设要求的四个数．

综上所述,n的最小值为1006．

16．由于x1,x2,…,x2012都是正整数,且x1＜x2＜…＜x2012,所以x1≥1,x2≥2,…,x2012≥2012．

综上,满足条件的所有正整数n为1,2,…,2012．

17．将所写数之和记为S;分别为三色点赋值:红0,蓝1,绿2,将所赋的值之和记为T．

注意到,两端点异色弧上所写数等于端点两数之和．

于是,S＝2T－A,其中,A为两端点同色弧的端点赋值总和．

又T＝0×40＋1×30＋2×20＝70,显然,可使蓝点互不相邻,绿点互不相邻．

此时,A＝0,Smax＝140;

当蓝色、绿色分别连成一段时,A最大,有Amax＝(1＋1)×29＋(2＋2)×19＝134．

此时,Smin＝6．