第25讲归纳与猜想，探索数独游戏的智力潜能

“数独”是“独立数字”的省略,意为每个方格都是独立的个位数．“数独”是一种智力游戏,它要在事先给定部分数字的9个九宫格中,填入1～9的数字,让每个数字在每行、列及九宫格里都只出现一次．20世纪70年代,“数独”雏形发表在美国一家数学逻辑游戏杂志上,从此风靡全球．

知能概述

当一个问题涉及相当多的乃至无穷多的情形时,我们可以从问题的简单情形或特殊情况入手,通过对简单情形或特殊情况的观察试验,从中发现一般规律并作出某种猜想,从而找到解决问题的途径或方法．

观察是解决问题的先导,发现往往是从观察开始的,归纳与猜想是建立在细致而深刻的观察基础上的．

问题解决

例1　观察以下两组数

5,9,13,17,21,25,29,33,…

4,7,10,13,16,19,22,25,…

它们中间第15对相同的数是_________．

(吉林省竞赛题)

解题思路　从分析每串数的特征入手．

我们的科学知识,是通过未经证明和不可证明的预言,通过猜测,通过对问题的尝试性解决,通过猜想而进步的．

——波普尔

孪生素数猜想

3,5,7,11,13,17,19都是素数,3和5,5和7,11和13,17和19是成对的素数,它们的差都为2,可以说是一对对双胞胎,把它们叫作孪生素数．

猜想:存在无穷多个素数P,使得P＋2也是素数．

这就是与哥德巴赫猜想齐名,集令人惊异的简单表述与令人惊异的复杂证明于一身的著名猜想——孪生素数猜想．

例2　古希腊人常用小石子在沙滩上摆成各种形状来研究数．比如:他们研究过图①中的1,3,6,10,…由于这些数能够表示成三角形,故将其称为三角形数．类似地,称图②中的1,4,9,16,…这样的数为正方形数．下列数中,既是三角形数,又是正方形数的是(　)．

A．289　B．1024　C．1225　D．1378

解题思路　把图①,图②中的第n个图中的石子数用n的代数式表示．

例3　化简

(江苏省竞赛题)

解题思路　先考察n＝1,2,3时的简单情形,然后作出猜想,这样化简的目标更加明确．

例4　如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要_________枚棋子,摆第n个图案需要_________枚棋子．

(山东省青岛市中考题)

解题思路　观察数值,从特殊到一般;或分割图形,从部分到整体,因视角的变换,图形有多种分割方式．

观察时应调整观察的角度,从点到面,从局部到整体,以利于观察出有一定隐蔽性的内在规律．

规律探究题,常按照一定的顺序给出一系列量,要求根据已知量找出一般规律,解题的关键是把变量和序号联系起来．

图形生长规律探寻可从以下方面入手:

(1)整理数据,分析数据;

(2)把握图形结构、生长方式．

例5　图(a),(b),(c),(d)都被称作平面图．

(1)数一数每个图各有多少个顶点,多少条边,这些边围出了多少区域,将结果填入表中[其中(a)已填好]．

(2)观察表,推断一个平面图的顶点数、边数、区域数之间有什么关系?

(3)现已知某一平面图有999个顶点和999个区域,试根据(2)中推断出的关系,确定这个图有多少条边．

(“华罗庚金杯”少年数学邀请赛试题)

解题思路　从特殊情况入手,仔细观察、分析、试验和归纳,从而发现其中的共同规律．

例6　自然数按下表的规律排列:

(1)求上起第10行,左起第13列的数;

(2)数127应在上起第几行、左起第几列?

(北京市“迎春杯”竞赛题)

分析与解　“取其一翼”“直击命门”“奇取中军”,巧用兵法,妙破数阵．经观察可得这个自然数表的排列特点:①第一列的每一个数都是完全平方数,并且恰好等于它所在行数的平方,即第n行的第1个数为n2;②第一行第n个数是(n－1)2＋1;③第n行中从第一个数至第n个数依次递减1;④第n列中从第一个数至第n个数依次递增1．

这样可求:(1)上起第10行,左起第13列的数应是第13列的第10个数,即[(13－1)2＋1]＋9＝154．

(2)数127满足关系式127＝112＋6＝[(12－1)2＋1]＋5,即127在左起12列,上起第6行的位置．

例7　观察按下列规则排成的一列数:

(1)在(※)中,从左起第m个数记为F(m),当F(m)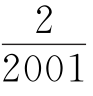＝时,求m的值和这m个数的积;

历史上著名的数学家欧拉曾研究过正多面体,他惊奇地发现了正多面体的顶点数(V)、面数(F)、棱数(E)存在一个奇妙的相等关系:V＋FE＝2,史称“欧拉公式”,它不仅在数学方法上有所创新,而且推动了现代数学的重要分支——拓扑学的发展．

观察、归纳出来的结论一般来说只是一种猜想,它是否正确,还有待于进一步证明．

1644年,法国修道士麦森宣布MP＝2P－1型的数,当P＝2,3,5,7,13,17,31,67,127,257时都是素数．1903年,美国著名数学家科尔做了一次无声的学术报告,他在黑板上先算出267－1,接着又把193707721×761838257287用竖式算了一遍,两个结果完全相同,顿时会场上响起雷鸣般的掌声,这个反例纠正了人们长达二百多年的错误．

(2)在(※)中,未经约分且分母为2的数记为c,它后面的一个数记为d,是否存在这样的两个数c和d,使cd＝2001000?如果存在,求出c和d;如果不存在,请说明理由．

(湖北省竞赛题)

分析与解　按分母递减而分子递增的变化规律,对原数列恰当分组,明确每组中数的个数与分母的关系．

递推

归纳总是与递推联系在一起的,所谓递推,就是在归纳的基础上,发现每一步与前一步或前几步之间的联系,更容易发现规律或证明通过归纳所猜测的规律的正确性．

例8　一楼梯共有n级台阶,规定每步可以迈1级或2级或3级,设从地面到台阶的第n级,不同的迈法为an种,当n＝8时,求a8．

(河南省竞赛题)

解题思路　先求出当n＝1,2,3,4时,a1,a2,a3,a4的值,解题的关键是,从某级开始,寻找an与an－1,an－2,an－3的联系．

爱因斯坦说过:你能观察到目前的什么现象,不仅取决于你的肉眼,还取决于你运用什么样的思维,思维决定了你到底能观察到什么,对于下图,读者你观察到了什么?

解决一类与自然数n相关的问题或涉及操作次数较多的问题时,通过寻找递推关系式,运用初始条件,化难为易,是一种从有限认识无限的重要方法．

1．分形之美

(1)把边长为1的正方形的每条边三等分,连成一个3×3的网格,再将中间的小正方形挖去,如图a①,则剩余阴影部分的面积为_________．如图a②,对图a①中每个阴影正方形执行同样的操作——分成3×3的小正方形并挖去中间一个,则剩余阴影部分的面积为_________．类似地做下去,如图a③,④,…,得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样．它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”．

(第1题图a)

(2)一个棱长为1的正方体木块,将其中的每个面分成3×3的正方形,然后沿与棱平行的面将中间完全“挖空”,如图b①,则剩余木块(阴影部分)的体积为________．

(第1题图b)

在图b①的基础上进行类似的操作,如图b②,③,经过多次操作后得到的几何体被称为“门杰海绵”．图b③是经过3次操作后得到的立体图,则图b③中木块的体积为________．

(《时代学习报》数学文化节试题)

2．斐波那契数列与上台阶问题

众所周知,数列1,1,2,3,5,8,13,21,…称为Fibonacci数列,其规律是:每个数等于它前面两数之和,即an＝an－1＋an－2．据说这个数列源自“大兔生小兔”的故事．

(第2题)

①:假设每次可上1级或2级台阶,则7级台阶共有_________种上法．

②:假设每次可上1级、2级或3级台阶,则5级台阶共有_________种上法．

(《时代学习报》数学文化节试题)

3．将奇数依顺序排成如图所示数阵,从上到下称为行,图中数11为第3行从左往右数的第2个数,数29为第4行第6个数,那么,2003为第________行第________个数．

(江西省竞赛题)

(第3题)

(第4题)

4．将正整数从1开始按图所示的规律排成一个数阵,其中,2在第一个拐弯处,3在第二个拐弯处,5在第三个拐弯处,7在第四个拐弯处……则在第2007个拐弯处的数是_________．

(北京市竞赛题)

5．观察下列等式:

12＝1,

12－22＝－3,

12－22＋32＝6,

12－22＋32－42＝－10,

……

按此规律,第n个等式为________．

(陕西省高考试题)

6．古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为,记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:

三角形数

正方形数　N(n,4)＝n2,

五边形数

六边形数　N(n,6)＝2n2－n,

……

可以推测N(n,k)的表达式,由此计算N(10,24)＝________．

(湖北省高考试题)

7．有以下两个数串1,3,5,7,…,1991,1993,1995,1997,1999和1,4,7,10,…,1990,1993,1996,1999,同时出现在这两个数串中的数的个数共有(　)．

A．333　B．334　C．335　D．336

(“希望杯”邀请赛试题)

8．一列数按某规律排列如下:,…,若第n个数为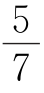,则n＝(　)．

A．50　B．60　C．62　D．71

(湖北省十堰市中考题)

9．令a＝0．123456789101112…998999,其中的数字是由依次写下正整数1至999得到的,则小数点右边第2007位数字是(　)．

A．0　B．4　C．5　D．6

(四川省竞赛题)

10．探索规律:31＝3,32＝9,33＝27,34＝81,35＝243,36＝729,…那么32005的个位数字是(　)．

A．3　B．9　C．7　D．1

(河南省竞赛题)

11．图中上边的4个图形呈现一定的规律性,根据这种规律,请你在下边给出的备选答案中选出一个最合理的答案作为上边的第五个图形(　)．

(第11题)

(武汉大学自主招生试题)

12．如图,A,B,C是固定在桌子上的三根立柱,其中A柱上穿有三个大小不同的圆片,下面的直径总比上面的大．现想将这三个圆片移动到B柱上,要求是每次只能移动一片(叫移动一次),被移动的圆片只能放入A,B,C三个柱之一且较大的圆片不能叠在小片的上面,那么完成这件事情至少要移动圆片的次数是(　)．

A．6　B．7　C．8　D．9

(第12题)

(重庆市竞赛题)

13．如图的图案均是用长度相同的火柴棍按一定的规律拼搭而成的:第1个图案需7根火柴,第2个图案需13根火柴……依此规律,第11个图案需多少根火柴?

(第13题)

(世界数学团体锦标赛试题)

14．将自然数按如图所示的顺序排列,在这样的排列下,数字3排在第二行第一列,13排在第三行第三列．问:1993排在第几行第几列?

(第14题)

(“华罗庚金杯”少年数学邀请赛试题)

15．在一列数中,a1＝0,a2＝1,从第2个数起,每个数的3倍等于这个数左右两个相邻的数之和,则这列数中的第2016个数被6除所得的余数．

(“希望杯”邀请赛试题)

16．将全体正整数按如下方式分组:{1,2},{3,4,5},{6,7,8,9},{10,11,12,13,14},…

(1)求第50组中最小的正整数;

(2)求满足下列条件的最大正整数:不大于2017,且是某组中最大的正整数．

(中法中学生数学交流试题)

17．若干个1与2排成一行:1,2,1,2,2,1,2,2,2,1,2,…规则是:第1个数是1,第2个数是2,第3个数是1．一般地,先写一行1,再在第k个1与第k＋1个1之间插入k个2(k＝1,2,3,…)．

试问:(1)第2005个数是1还是2?

(2)前2005个数的和是多少?

(3)前2005个数两两乘积的和是多少?

(江苏省竞赛题)

18．在2,3两个数之间,第一次写上＝5,第二次在2,5之间和5,3之间分别写上和＝4,如下所示:

第0次操作:2　3

第1次操作:2　5　3

第2次操作:2　　5　4　3

第3次操作:　……

第k次操作是在上一次操作的基础上,在每两个相邻的数之间写上这两个数的和的．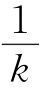

(1)请写出第3次操作后所得到的9个数,并求出它们的和;

(2)经过k次操作后所有数的和记为Sk,第k＋1次操作后所有数的和记为Sk＋1,写出Sk＋1与Sk之间的关系式;

(3)求S6的值．

(“希望杯”邀请赛试题)

例1　181　第一列数为4n＋1形式,第二列数为3n＋1形式,相同的数为12n＋1形式(n为正整数),当n＝15时,12×15＋1＝181．

例2　C　图①中第n个图共有石子1＋2＋…＋n＝(个),图②中第n个图共有石子n2(个),1225＝,1225＝352．

例3　原式＝102n．

例4　127　3n2＋3n＋1　列表填数,观察数值,体会从特殊到一般的数学思想．

a1＝7＝1＋6＝1＋1×6;

a2＝19＝1＋6＋12＝1＋(1＋2)×6;

a3＝37＝1＋6＋12＋18＝1＋(1＋2＋3)×6;

……

猜想an＝1＋(1＋2＋3＋4＋…＋n)×6＝3n2＋3n＋1,再将n＝6代入该代数式得127．

例5　(1)略;(2)顶点数＋区域数－边数＝1;(3)1997条．

例8　当n＝1时,a1＝1．当n＝2时,a2＝2．当n＝3时,a3＝4．则当n＝4时,若第一步1级,则其余3级有a3种方法;若第一步2级,则其余2级有a2种方法;若第一步3级,则其余1级有a1种方法．

故a4＝a3＋a2＋a1＝7,类似可得n＝5时,a5＝a4＋a3＋a2＝13;n＝6时,a6＝a5＋a4＋a3＝24;n＝7时,a7＝a6＋a5＋a4＝44;n＝8时,a8＝a7＋a6＋a5＝81．

1．(1)(2)

2．①21　②13

3．32　41　2003是数阵从上向下、从左往右数的第1002个数,前n行共有1＋3＋…＋(2n－1)＝n2个数,而312＝961,322＝1024,故2003位于第32行第1002－961＝41个数．

4．1008017　a1＝2,a2＝3,a3＝5,a4＝7,a5＝10,a6＝13,a7＝17,a8＝21,…,又a3＝a1＋3,a5＝a3＋5,a7＝a5＋7,…即后一拐弯数＝前一拐弯数＋后一拐弯次数．

9．C　1～9共9个数字;10～99共2×90＝180个数字;100～999共3×900＝2700个数字．由于2007－9－180＝1818,而1818÷3＝606,即第2007位数字为第606个三位数705的第3个数字．

10．A　34k＋1的个位数字是3．

11．A　题干每个单独图形中都有5个小图形元素．

12．B　an＝2n－1．

13．当数据规律不明显时,可从分析图形构成入手．为使图形结构清晰,可适当改变图形．

将图中各个图案右下角的一个正方形移除3根火柴后得如下图:

(第13题)

图中第1个图案需要横向火柴1＋1＝2(根),纵向火柴1＋1＝2(根),共需4根火柴;

第2个图案需要横向火柴1＋2＋2＝5(根),纵向火柴1＋2＋2＝5(根),共需10根火柴;

第3个图案需要横向火柴1＋2＋3＋3＝9(根),纵向火柴1＋2＋3＋3＝9(根),共需18根火柴;

……

第n个图案需要横向火柴的根数是1＋2＋3＋…＋n＋n＝,纵向火柴的根数也是,共需n(n＋3)根火柴．

故拼搭图中第11个图案需火柴11×(11＋3)＋3＝157(根)．

14．第n斜行中共有n个连续的自然数,其中最大的数是,第62斜行的最大数是＝1953,第63斜行的最大数是＝2016．因此,1993位于第63斜行．

又第63斜行中的数是由下向上递增的,左边第一个数是1954,则1993是位于第63斜行的由下向上数第1993－1954＋1＝40个位置的数,换成原图中行和列是第63－40＋1＝24行,第40列．

15．设这一列数是a1,a2,…,an,…,则这一列数的规律是3an＝an－1＋an＋1(n≥2),即

an＋1＝3an－an－1(n≥2)．

易知,这列数的前若干个是:0,1,3,8,21,55,144,…．可发现这列数的奇偶情况,由左向右,依次是:偶,奇,奇;偶,奇,奇;…的规律,并且是每3个数一循环．因为

2016÷3＝672,

故第2016个数为奇数．

再研究这列数被3除,所得的余数是:0,1,0,2;0,1,0,2;…的规律,并且每4个数为一循环．因为

2016÷4＝504,

故第2016个数被3除余2,这说明a2016是形式为3k＋2(k是0,1,2,…)的数,即

2,5,8,11,14,17,…

又因为a2016为奇数,所以a2016只能是其中的5,11,17,…中的数,而这些数被6除,所得的余数是5．

16．(1)显然,第1组中最小的正整数是1,第2组中最小的正整数是3,……,设第n组中最小的正整数为an,可归纳得a1＝1,a2＝3＝1＋2,a3＝6＝1＋2＋3,…,an＝1＋2＋…＋n＝,所以a50＝＝1275．

(2)设第n组中最大的正整数为bn,则有

因为b62＝＝2015＜2017,b63＝＝2079＞2017,所以2015是第62组中最大正整数．

17．(1)把该列数分为如下n组:

这n组共有1＋2＋…＋n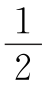＝n(n＋1)个数．当n＝62时,共有1953个数;当n＝63时,共有2016个数．可见,第2005个数位于第63组中,且不是最后一个数,从而第2005个数是2;

(2)在前2005个数中,共有62个1及2005－62＝1943个2．所以,前2005个数的和为62×1＋1943×2＝3948;

(3)不妨设这2005个数为a1,a2,…,a2005,其和为R,平方和为T,其两两乘积的和为S,则R＝a1＋a2＋…＋a2005＝3948,T＝＝62×12＋1943×22＝7834,S＝a1a2＋a1a3＋…＋a1a2005＋a2a3＋a2a4＋…a2a2005＋…＋a2004a2005．于是2S＝a1a2＋a1a3＋…＋a1a2005＋a2a1＋a2a3＋…＋a2a2005＋…＋a2005a1＋a2005a2＋…＋a2005a2004＝＝R2－T,从而S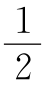＝(39482－7834)＝7789435．故所求的和为7789435．