图形面积计算方法及应用

我们如果只凭直观感受进行判断,那么很可能产生错觉或错误的判断,我们把看上去的情况和实际有偏差的图形,称之为错视图形．

知能概述

面积是平面几何中一个重要概念,计算图形面积是平面几何中最基本的问题之一,常用的计算方法有:和差法、运动法、等积变形法．

面积的计算主要是求一些非常规图形的面积,非常规图形面积的计算往往可转化为常规图形面积的计算．在转化的过程中,常用到恰当连线、图形割补、等积变形、线段比与面积比互化、代数化等技巧方法．

熟悉下列基本图形:

问题解决

例1　如图,若长方形APHM,BNHP,CQHN的面积分别为7,4,6,则阴影部分的面积是_________．

(“五羊杯”邀请赛试题)

解题思路　从寻找三角形与长方形面积关系入手．

几何学有形象化的好处,几何会给人以数学直观,不能把几何学等同于逻辑推理．只会推理,缺乏数学直觉,是不会有创造性的．

——吴文俊

两弯新月

如图,以直角三角形两直角边为直径向外作两个半圆,以斜边为直径向外作半圆,则三个半圆所围成的两个月牙形面积之和等于该直角三角形的面积．

这是古希腊数学家希波克拉底发现的定理．

例2　正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为(　)．

A．10　B．12　C．14　D．16

(广西壮族自治区南宁市中考题)

解题思路　延长AE,PK交于点H,把△DEK的面积转化为规则图形的面积之和或差;或恰当作出辅助线,运用等积变形转化问题．

例3　如图,设E,F分别是△ABC的边AC,AB上的点,线段BE,CF交于点D．已知△BDF,△BCD,△CDE的面积分别为3,7,7．求四边形AEDF的面积．

(青少年数学国际城市邀请赛试题)

解题思路　设S△DEF＝x,S△AEF＝y,把线段比转化为对应的三角形面积比．

例4　如图,已知△ABC中,,三角形PQR的面积为20cm2,求△ABC的面积．

(美国数学邀请赛试题)

解题思路　连BR,CP,把线段比转化为对应三角形面积比,分别把△APR,△BPQ,△QRC的面积用△ABC的面积表示．

求一些关系复杂的图形面积,代数化是一个重要技巧,利用代数化,能清晰明了地表示图形面积之间的关系,从而可以化解或降低问题的难度．代数化的常见形式是:

(1)设而不求,整体求解;

(2)借助方程、方程组．

促使面积比与对应线段比之间的相互转化,是求图形面积的一个常用技巧,解题的关键是加强对图形结构的分析,寻找共高或共底或共角的三角形．

如图①,

例5　如图①,已知正方形ABCD的面积为1,M为AB的中点．求图中阴影部分的面积．

(湖北省武汉市竞赛题)

解法1　如图①,S△AMD＝S△AMC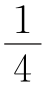＝,S△AMG为公共部分,所以S△AGD＝S△MCG,因为△AMG与△AMD的高相等(以A为顶点作高),△MCG与△MCD的高相等(以C为顶点作高),

解法2　如图②,连接GB,由正方形的对称性得S△ABG＝S△AGD,

又

所以

解法3　如图③,连接BD,BG,设BD,AC交于点O,S△AMG＝x,

因为

所以　S△GOD＝S△AOD－S△AGD＝S△AMD－S△AGD＝S△AMG＝x．

又　S△BOG＝S△GOD＝x,S△BMG＝S△AMG＝x,

因为　S△AOB＝S△AGM＋S△GOB＋S△BMG,

即　＝x＋x＋x,所以　x＝．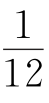

所以　S阴影＝S△AGD＋S△MCG＝2(S△AMD－S△AMG)＝．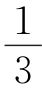

例6　直角三角形的两条直角边长分别为5和12,斜边长为13,P是三角形内或边界上的一点,P到三边的距离分别为d1,d2,d3,求d1＋d2＋d3的最大值和最小值,并求当d1＋d2＋d3取最大值和最小值时,P点的位置．

(“创新杯”邀请赛试题)

充分利用正方形的特征、中点,探寻知识的关联,从特殊到一般,从面积比到代数化,由点到面,生成例5的不同解法．

解　如图所示,在△ABC中,∠C＝90°,BC＝5,AC＝12,BA＝13,P到BC,CA,AB的距离分别为d1,d2,d3,连接PA,PB,PC,由三角形的面积公式知:

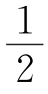×5d1＋×12d2＋×13d3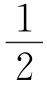＝×5×12,即5d1＋12d2＋13d3＝60．

显然有5(d1＋d2＋d3)≤5d1＋12d2＋13d3≤13(d1＋d2＋d3),

故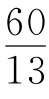≤d1＋d2＋d3≤12．

当d2＝d3＝0时,有d1＋d2＋d3＝12,即d1＋d2＋d3取最大值时,P与A重合;当d1＝d2＝0时,有d1＋d2＋d3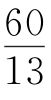＝,即d1＋d2＋d3取最小值时,P与C重合．

井田

一块不规则的四边形田地,在每条边都取三等分点,再把两组对边上的三等分点连接起来,成为一个“井”字形,“井”字把这块田分成了九小块．

例7　(1)如图①,已知四边形ABCD中,E,F是DC边的三等分点,G,H是AB边的三等分点．

求证:S四边形GHFE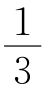＝S四边形ABCD．

(2)如图②,已知四边形ABCD中E,F,G,H,M,N,R,S分别是四边三等分点．

求证:S阴影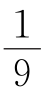＝S四边形ABCD．

(3)请你提出类似问题．

解题思路　作辅助线,充分利用等分点,把四边形面积转化为三角形面积．

有些几何问题,虽然题目中没有直接涉及面积,但由于面积关联着边、角两个重要元素,所以我们可从面积角度思考问题,这就是常说的面积法．

用面积法解题的基本步骤是:

(1)用不同方法或从不同角度计算某一图形面积,得到一个含边或含角的关系式．

(2)化简这个面积关系式,直至得到求解或求证的结果．

1．(1)如图a,一个大正方形被2条线段分割成2个小正方形和2个长方形,如果S1＝75cm2,S2＝15cm2,那么大正方形的面积S＝_________cm2．

(第1题)

(江苏省竞赛题)

(2)如图b,大长方形中有5个小长方形面积的数值已标出,那么,左上角小长方形的面积是_________．

(“华罗庚金杯”少年数学邀请赛试题)

2．如图,△ABC中,∠ACB＝90°,AC＝1厘米,AB＝2厘米．以B为中心,将△ABC顺时针旋转,使得点A落在边CB延长线上的A1点,此时点C落到点C1．则在旋转中,边AC变到A1C1所扫过的面积为_________平方厘米(结果保留π)．

(第2题)

(“希望杯”邀请赛试题)

3．如图,对于一个8×5的长方形,图中的阴影部分的面积为________．

(美国数学竞赛题)

(第3题)

(第4题)

4．正方形ABIJ,BCGH,CDEF的边长依次为10厘米、8厘米和6厘米．它们和一个长方形LTJK放在一起组成如图所示的阴影多边形．其中A,B,C,D在一条直线上,K,J,I也在一条直线上．已知KL＝5厘米,KD平分阴影图形的面积,则KJ＝________厘米,阴影多边形的面积＝_________厘米2．

(“希望杯”邀请赛试题)

5．如图,大圆中有4个面积相等的小圆,已知小圆半径为5cm,大圆半径等于小圆直径,则空白部分的面积是_________cm2(π取3)．

(世界数学团体锦标赛试题)

6．如图所示,AF＝7cm,DH＝4cm,BG＝5cm,AE＝1cm．若正方形ABCD内的四边形EFGH的面积为78cm2,则正方形的边长为________cm．

(世界数学团体锦标赛试题)

(第5题)

(第6题)

(第7题)

7．如图所示,在正方形ABCD的BC边上有一动点E,以DE为边作矩形DEFG,且FG边通过点A,请问当点E从点B移动到点C的过程中矩形DEFG的面积是如何变化的?(　)

A．一直变大　B．一直变小　C．先变小后变大

D．先变大后变小　E．保持不变

(国际中小学数学能力检测试题)

8．如图,已知正方形ABCD和CEFG的边长分别为m,n,那么△AEG的面积的值(　)．

A．只与m的大小有关　B．只与n的大小有关

C．与m,n的大小都有关　D．与m,n的大小都无关

(江苏省竞赛题)

(第8题)

(第9题)

(第10题)

9．如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BC＝4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为(　)．

A．3　B．4　C．6　D．8

(全国初中数学竞赛题)

10．如图,在△ABC中,∠BAC＝90°,AB＝12cm,AC＝6cm,D,E分别为AB,AC上的点,且AD＝8cm,AE＝5cm．连接BE,CD相交于点G,则四边形ADGE的面积是(　)．

A．21．5　B．22．5　C．23．5　D．24．5

(“华罗庚金杯”少年数学邀请赛试题)

11．如图,若P为平行四边形ABCD内一点,且S△PAB＝5,S△PAD＝2,则S△PAC＝(　)．

A．5　B．4　C．3　D．2

(湖北省武汉市竞赛题)

(第11题)

(第12题)

12．如图,延长△ABC的三边,使得BD＝AB,CE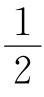＝BC,AF＝CA,则△DEF与△ABC的面积之比是(　)．

A．3∶1　B．7∶2　C．10∶3　D．13∶4　E．14∶15

(美国数学竞赛题)

13．皮克公式

各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形,如何计算它的面积?奥地利数学家皮克(G．Pick,1859—1942)证明了格点多边形的面积公式:S＝ma＋nb－1,其中m,n为常数．a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积．

(1)在下面的方格纸中各画出一个面积为6的格点多边形,依次为三角形、平行四边形;

(2)利用(1)中的格点多边形确定m,n的值．

(浙江省宁波市中考题)

14．如图,已知ABCD是长为3、宽为1的长方形,BE＝EG＝GC,AH＝2HD,AG,AC,BH,EH交成阴影四边形PNQM,求四边形PNQM的面积．

(“华罗庚金杯”少年数学邀请赛试题)

(第14题)

(第15题)

(第16题)

15．如图,△ABC中,已知,求的值．

(“华罗庚金杯”少年数学邀请赛试题)

16．如图,已知△ABC的面积为1,D,E为AC的三等分点,F,G为BC的三等分点．求:

(1)四边形PECF的面积;

(2)四边形PFGN的面积．

(“希望杯”邀请赛试题)

17．如图,在△ABC中,AB＝13,BC＝14,CA＝15,P是△ABC内部或边界上的一点,P到三边AB,BC,CA的距离分别是x,y,z,记u＝x＋y＋z．

(1)使得u＝13的点P是否存在?若存在,请找出所有满足条件的P点;若不存在,请说明理由．

(第17题)

(2)使得u＝12．5的点P是否存在?若存在,请找出所有满足条件的P点;若不存在,请说明理由．

(“创新杯”邀请赛试题)

18．如图,△ABC中,AB＝AC,∠BAC＝120°．△ADE是正三角形,点D在BC边上,BD∶DC＝2∶3．当△ABC的面积是50平方厘米时,求△ADE的面积．

(第18题)

(日本算术奥林匹克决赛试题)

有时直接求图形面积有困难,可通过平移、旋转、割补等方式,将图形或部分图形运动起来,把图形转化为易观察或易解决的形状,动中求解．

类似于第18题,有一些涉及30°,45°,60°,90°,120°的图形问题,由于这些角的度数的整数倍形成360°,因此运用旋转一周的方法有时能简捷解决问题,并富有美感．

例1　8．5　S阴影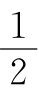＝(7＋4＋6)＝8．5．

例2　D

如图,连DB,GE,FK,则∠DBA＝∠GEB＝45°,

∴DB∥GE,得S△GED＝S△GEB,

同理GE∥FK,得S△GEK＝S△GEF．

∴S△DEK＝S△GED＋S△GEK＝S△GEB＋S△GEF＝S正方形BEFG＝16．

(例2)

例7　(1)如图①,连FG,DG,FB,DB,

∵S△EGF＝S△EGD,S△HFG＝S△HFB,

∴S四边形DGBF＝2S四边形GHFE．　①

又∵DE＝EF＝FC,AG＝GH＝HB,

∴S△DBC＝3S△FBC,S△DBA＝3S△DGA,

∴S四边形ABCD＝3(S△FBC＋S△DGA),

(例7)

得S△FBC＋S△DGA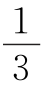＝S四边形ABCD．　②

①＋②,得S四边形ABCD＝2S四边形GHFE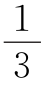＋S四边形ABCD,故S四边形GHFE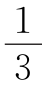＝S四边形ABCD．

(2)可证明O,P与K,T分别是EG,FH的三等分点,进一步可证明S四边形OPKT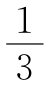＝S四边形GHFE,

从而S阴影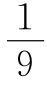＝S四边形ABCD．

(3)下面问题供参考:

如图②是一个凸四边形,各边上的点都是五等分点．请在25小块四边形中寻找面积等于四边形面积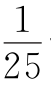的那一块,并加以证明．

(例7)

1．(1)108　(2)12

2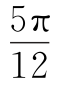．如图,边AC变到A1C1所扫过的面积＝部分圆环CDAD1C1的面积．

3．6如图,过长方形的对称中心作两边的平行线．

(第2题)

(第3题)

(第4题)

4．8　240　作出如图所示的辅助线,完形得长方形KPDM,设KJ＝x,则5x＝16＋24．

5．150　如图,因为1与2,3与4,5与6,7与8,9与10,11与12部分的面积相等,所以空白部分的面积为半个大圆的面积,即0．5×π×102＝50π＝150(平方厘米)．

(第5题)

(第6题)

6．12　用竖直线和水平线将正方形分割为如图所示的5个长方形,正方形面积为(78－12)×2＋12＝144cm2．

7．E　连接AE,S矩形DEFG＝S正方形ABCD．

13．(1)略　(2)m＝1,n＝．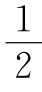

14．连接HG,HC和AE,见图．

在四边形ABCH中,由三角形面积公式,可知:

(第14题)

(①式表示4个三角形面积成比例,常被称为共边定理．)由①和已知条件可得:

类似地,由共边定理,在四边形AEGH中,可得三角形EGN的面积是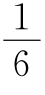;在四边形AECH中,可得三角形ECQ的面积是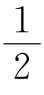;在四边形ABGH中,三角形BGP的面积是．

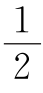所以,四边形PNQM的面积＝

于是有13x＋14y＋15z＝168(*)．

(1)若x＋y＋z＝13,则13x＋13y＋13z＝169＞13x＋14y＋15z,显然矛盾,故不存在这样的点,使u＝13;

(2)若x＋y＋z＝12．5,将(*)式化为14(x＋y＋z)＋z－x＝168,于是x－z＝7,作直线DE∥AB,且使DE与AB的距离等于7,DE分别交AC,BC于点D,点E,再作∠CDE的角平分线,交CE于点T,则线段DT上任一点P都满足条件．

18．直接解题有困难,将△ABC绕A点顺时针旋转120°,240°拼成正△MBC,则正△ADE变为正△AD1E1和正△AD2E2．易知六边形DED1E1D2E2是正六边形,△DD1D2是正三角形,S△DD1D2＝3S△ADE(图②)．因此,设法由正△MBC面积为150,求出△DD1D2的面积,问题就解决了．

因为　BD∶DC＝CD1∶D1M＝MD2∶D2B＝2∶3,

所以连DM(如图②),则

(第18题)

S△MBD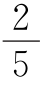＝S△MBC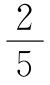＝×150＝60(平方厘米),

而S△D2BD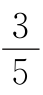＝S△MBD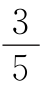＝×60＝36(平方厘米)．

同理可得S△MD1D2＝S△DCD1＝36(平方厘米)．

因此S△DD1D2＝150－3×36＝42(平方厘米),

S△ADE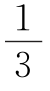＝S△DD1D2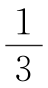＝×42＝14(平方厘米)．