多边形边角及对角线的基本概念及性质

1796年,年仅19岁的高斯给出了正十七边形可以用尺规作图的证明．这一问题的证明不仅震撼了数学界,也震撼了高斯自己的心灵．高斯逝世后,人们按照他的遗嘱,在他的雕像下面建立了一座正十七边棱柱的底座．1989年,第三十届国际数学奥林匹克在高斯曾执教的哥廷根大学举行,也是用正十七边形作为会徽,以示纪念．

知能概述

边、角、对角线是多边形中最基本的概念．

多边形的性质常转化成三角形来说明,连对角线或向外补形,是把多边形问题转化为三角形问题来解决的基本策略．

多边形内角和随着边数的变化而改变,而多边形的外角和性质反映出更本质的规律:外角和是360°的一个常数,把内角问题转化为外角问题,以静制动是解多边形相关问题的常用技巧．

问题解决

例1　(1)如图①,∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝_________．

(河南省竞赛题)

(2)如图②,∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝_________．

(全国初中数学竞赛题)

解题思路　对于(1),运用三角形外角的性质,或连线运用对顶三角形的性质,把分散的条件加以集中;对于(2),将问题转化为四边形、三角形内角和的计算．

你,大自然,我的女神,我要为你的规律而献身．

——高斯

甜蜜的问题

20世纪30年代几位数学家在讨论着这样一个问题:“平面上任给5个点,若其中任意3个点不共线．求证:必有4点能构成凸四边形．”

数学家埃丝特·克莱因证明了这个问题,恩德雷·麦凯证明了:为保证能构成凸五边形至少需要9个点．他们因上述问题而结为百年之好．大数学家保罗·埃尔德什给这问题起了一个好听的名字——“甜蜜的问题”．

例2　凸多边形恰好有三个内角是钝角,这样的多边形边数的最大值是(　)．

A．4　B．5　C．6　D．7

(全国初中数学联赛题)

解题思路　把凸多边形内角问题转化为外角问题．

例3　美在其中　有一副由正三角形与正方形(它们的边长相等)组成的拼板玩具,用它们可以拼成若干种凸多边形(任意一个内角都小于180°的多边形)．这类多边形中的五边形、六边形和七边形如图所示:

这类多边形中边数最多的是几边形?试画出一个这样的多边形．

(《时代学习报》数学文化节试题)

解题思路　正三角形和正方形的内角分别为60°和90°,故由它们拼成的凸多边形的内角只可能是60°,90°,120°和150°这四种,这是解本例的关键．

例4　在一个凸五边形内选取一点,将其与各顶点相连．在所有的10条线段(5条连线以及五边形的5条边)中,最多可有多少条线段的长度为1?

(俄罗斯竞赛题)

解题思路　所有10条线段的长度能均为1吗?以退为进,构造符合要求的图形．

善于综合运用平行线、三角形、多边形的相关知识,并能充分认识图形,是现阶段解决相关问题的基础．

在《骑士》中,一队人马向左,一队人马向右,相反相成,相映成趣．在埃舍尔的镶嵌图案中,他用几何学中的反射、旋转、平移等变换来获得更多的变化图案．杨振宁著作《基本粒子发现简史》的封面用的就是这幅画作．这幅作品与物理学中对称性的结构对应论相吻合．

例5　设有一个凸多边形,除去一个内角以外,其余n－1个内角和为1993°,求n的值．

(安徽省竞赛题)

解法1　设除去的内角度数为x,由题意得(n－2)180＝1993＋x．

∴

∵n－2为整数,且0＜x＜180．

∴13＋x＝180,得n－2＝11＋1,从而n＝14．

解法2　∵0°＜x＜180°,

∴

解得

∵n为正整数．∴n＝14．

例6　一个凸11边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成,求此凸11边形各个内角的大小,并画出这样的凸11边形的草图．

(全国初中数学竞赛题)

分析与解　设凸11边形的内角中有60°,90°,120°,150°的个数分别为x,y,z,s．列出它们满足的关系式,并求出x,y,z,s的值．

设此凸11边形的各个内角中有x个60°,y个90°,z个120°,s个150°,

依题意有

由①得s＝11－x－y－z,代入②,化简得3x＋2y＋z＝1,

因为x,y,z均为非负整数,所以x＝y＝0,z＝1,故s＝10．

则这个凸11边形有一个内角是120°,有10个内角都是150°．

大自然的青

自然界中的对象已经提供并且还在提供着激励数学发现的模型,数学是我们用来试图了解、解释和再现自然现象的手段．

平面镶嵌就是平面图形无缝隙又不重复地铺满整个平面．

镶嵌的实质在于,围绕一点拼在一起的若干个多边形的内角和为360°．

对于例6,可进一步思考:用边长相等的正三角形和正方形(无重叠无间隙)拼凸多边形,能拼成怎样的凸多边形?

其实,要得到完整的解答,需将问题转化为解方程组．

六边形是备受自然界青睐的基本图形之一,干裂的土地、晶体结构、雪花形状、三重联结、摆放物体、蜂房结构等,可以发现六边形在自然界中的广泛存在形式．

例7　定义:六个内角相等的六边形叫等角六边形．

(1)研究性质

①如图①,等角六边形ABCDEF中,三组正对边AB与DE,BC与EF,CD与AF分别有什么位置关系?证明你的结论;

②如图②,等角六边形ABCDEF中,如果有AB＝DE,则其余两组正对边BC与EF,CD与AF相等吗?证明你的结论;

③如图③,等角六边形ABCDEF中,试判断AB＋BC与DE＋EF的大小,并证明你的结论．

(2)探索判定

三组正对边分别平行的六边形,至少需要几个内角为120°,才能保证该六边形一定是等角六边形?

(浙江省台州市中考题)

解题思路　经计算得等角六边形每一内角为120°,120°给人以丰富的联想,通过对内分割或向外补形,将六边形问题转化为基本图形或特殊三角形、特殊四边形．

1．(1)一个多边形一共有14条对角线,则它的内角和为_________．

(“五羊杯”竞赛题)

(2)从凸n边形的一个顶点出发引出的所有对角线把这个凸n边形分成了m个小三角形,若m等于这个凸n边形对角线条数的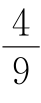,则此n边形的内角和为________．

(“希望杯”邀请赛试题)

2．正方形ABCD的内部有17个点,它们与正方形的4个顶点共计21个点,其中任意三点都不共线,以这21个点为顶点,将该正方形剪成小三角形,最多可以剪出_________个小三角形,此时共剪_________刀．

(“希望杯”邀请赛试题)

研究几何图形,我们往往先给出这类图形的定义,即按照一定规则的约定,用下定义的方式给出一个新图形的概念,运用新定义的图形概念探索新图形的性质,并运用新图形的性质解决问题．

例7从边、角元素出发,研究新图形的性质,探索其判定方法．由易到难,环环相扣,每一问题的解决都为下面新问题的探索积累经验和提供思考方向．

3．如图是一个多边形,则∠A1＋∠A2＋∠A3＋…＋∠A23＋∠A24的度数是_________．

(世界数学团体锦标赛试题)

(第3题)

4．用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面,设正多边形的边数为x,y,z,则的值为_________．

(四川省竞赛题)

5．一个多边形截去一个(三角形状的)角后,形成另一个多边形,其内角和是3060°,则原多边形是________边形．

(《时代学习报》数学文化节试题)

6．凸n边形恰有7个钝角,这7个钝角的和等于1100°,则n＝________．

(国际中小学数学能力检测题)

7．凸n边形中有且仅有两个内角为钝角,则n的最大值是(　)．

A．4　B．5　C．6　D．7

8．已知α是一个凸n边形的一个内角,和它对应的外角为β,除α外,其余内角的和为p°,除β外,其余外角的和为q°．若p＝13q,则n的值为(　)．

A．13　B．15　C．20　D．22

(“希望杯”邀请赛试题)

9．如图,∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝(　)．

A．100°　B．120°　C．150°　D．180°

(江苏省南京市竞赛题)

(第9题)

(第10题)

10．如图,将六边形ABCDEF沿直线GH折叠,使A,B落在六边形CDEFGH的内部,则下列结论一定正确的是(　)．

A．∠1＋∠2＝900°－2(∠C＋∠D＋∠E＋∠F)

B．∠1＋∠2＝1080°－2(∠C＋∠D＋∠E＋∠F)

C．∠1＋∠2＝720°－(∠C＋∠D＋∠E＋∠F)

D．∠1＋∠2＝360°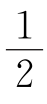－(∠C＋∠D＋∠E＋∠F)

(湖北省武汉市竞赛题)

11．在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的边数为(　)．

A．12　B．12或13

C．14　D．14或15

(江苏省竞赛题)

12．一张三角形纸片的长为1的边仅与一个边长为1的正12边形纸片的一条边重合,平放在桌面上,则所得到的凸多边形的边数一定不是(　)．

A．11　B．12　C．13　D．14

(北京市竞赛题)

13．(1)如图①,求∠A1＋∠A2＋…＋∠A8的度数．

(《时代学习报》数学文化节试题)

(第13题)

(2)如图②,求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠J的度数．

(天津市竞赛题)

14．如图,在凸六边形ABCDEF中,已知∠A＋∠B＋∠C＝∠D＋∠E＋∠F．试证明:该六边形必有两条对边是平行的．

(第14题)

(俄罗斯萨温市竞赛题)

15．美国华盛顿大学研究团队卡西·曼夫妇在2015年发现了一种新的不规则五边形(如图①),相互组合后可完全铺满平面(如图②),不会出现重叠或任何空隙,是全球第15种能做到此效果的五边形,而距上次发现类似效果的五边形已时隔30年,这项发明相当于在科学领域中寻获了新原子粒子．设此五边形ABCDE中AE＝10cm,则此五边形周长为多少?

(国际少年数学精英大会试题)

(第15题)

16．有四个边长分别为3cm,4cm,5cm的木三角形,用所有这些三角形能拼成多少种凸多边形(只需画出凸多边形,不需要证明)．

(伊朗几何奥林匹克试题)

17．把一个多边形沿着几条直线剪开,分割成若干个多边形．分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1．3倍．问:(1)原来的多边形是几边形?

(2)把原来的多边形分割成了多少个多边形?

(日本算术奥林匹克试题)

18．已知凸n边形A1A2…An(n＞4)的所有内角都是15°的整数倍,且∠A1＋∠A2＋∠A3＝285°,求n的最大值．

(世界数学团体锦标赛试题)

19．凸n边形中最多有多少个内角等于150°?请说明理由．

(全国初中数学竞赛题)

例1　(1)360°　连BC,则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝四边形EFBC的内角和＝360°．

(2)540°　∠A＋∠C＋∠1＋∠F＝360°,∠B＋∠D＋∠2＋∠G＝360°,

又∠1＋∠2＝180°＋∠E,由此得∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°＋360°－180°＝540°．

例2　C　设凸多边形的边数为n(n为自然数),由题意知n个外角中恰好有三个是锐角,那么其余n－3个外角将是钝角或直角,而外角中钝角的个数不超过3,即n－3≤3,n≤6,故n的最大值为6．

(例1)

例3　凸n边形的内角和为(n－2)×180°．若n≥13,则其内角和至少为(13－2)×180°＝1980°,从而各内角的平均度数大于150°,故这类凸多边形的边数n≤12．当n＝12时,(n－2)×180°＝1800°,这时该凸多边形各内角都等于150°,这样的凸十二边形是存在的．

例4　先证明:不可能所有10条线段的长度均为1．

假设不然．设有五边形ABCDE,O为其内部一点,使得所有的10条线段长度均为1,如图①．

(例3)

于是,△OAB,△OBC,△OCD,△ODE,△OEA均为正三角形．

故∠AOB＝∠BOC＝∠COD＝∠DOE＝∠EOA＝60°．

注意到,这些角的度数之和应为360°．但与5×60°＝300°矛盾．

(例4)

再举例说明:可以有9条线段长度为1,如图②．

在平面上取定点A与O,使它们的距离为1,再依次取点B,C,D,E,使得△OAB,△OBC,△OCD,△ODE均为正三角形．此时,点O必在凸五边形ABCDE内部,且所有的10条线段中,仅有AE长度不为1．

例7　(1)①略

②如图,延长BA,ED,EF,BC,两两分别相交于点P,点Q,则四边形EPBQ为平行四边形,△AFP,△DCQ都为等边三角形．

∴PB＝EQ,即AB＋AP＝ED＋DQ,

∴AB＋AF＝ED＋DC．

故AF＝DC,同理BC＝EF．

③同②,向外补形可证得AB＋BC＝DE＋EF．

(2)至少需要三个内角为120°．

(例7)

7．B

8．D　设∠α＝x°,∠β＝180°－x°．(n－2)180°－x°＝13(360°－180°＋x),n＝＋15,n,都为整数,x＜180,x＝90,n＝22．

9．D　连AC,EF,利用对顶三角形性质计算．

10．B　设FA的延长线与CB的延长线相交于P,GA′的延长线与HB′的延长线相交于P′,由对称性知,∠1＝2∠APP′,∠2＝2∠BPP′,

∴∠1＋∠2＝2∠APB．

又∠APB＝540°－(∠C＋∠D＋∠E＋∠F),

∴∠1＋∠2＝1080°－2(∠C＋∠D＋∠E＋∠F)．

11．D　设这个多边形为n边形,由2002°＜(n－2)×180°＜2002°＋360°,得13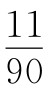＜n＜15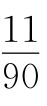,n＝14或15．

12．D　12边形和三角形加起来一共有15条边,其中重合的两条边肯定不是新的凸多边形的边,因此新的凸多边形的边最多为13条．

易知,正12边形纸片每个内角为＝150°．

(第10题)

若拼接的△ABC中,BC＝1,∠ABC＝∠ACB＝90°,拼接后是个11边形;

若拼接的△ABC中,BC＝1,∠ABC＝30°,∠ACB＜30°,拼接后是个12边形;

若拼接的△ABC中,BC＝1,∠ABC＜30°,且∠ACB＜30°,拼接后是个13边形．

因此所得到的凸多边形的边数一定不是14．

13．(1)360°　连A2A5,A5A8．

(2)1080°　连DE,BG,原式＝六边形CDEFIJ的内角和＋四边形ABGH的内角和．

14．可以证明CD∥AF．

15．(1)观察图①,可得∠E＝90°,2∠B＋∠E＝360°,由此得∠B＝135°,又

由此得∠A＝105°,∠D＝150°,∠C＝60°．

(第15题)

(2)在图②中,连接AD,BD,作DP⊥AB与AB交于点P,由图①可知AE＝DE＝BC,CD＝2AE＝2DE＝2BC,故∠1＝∠2＝45°,从而∠3＝60°,∠4＝30°．

(3)在△BCD中,由∠C＝60°和CD＝2BC得∠8＝90°,从而∠7＝30°,∠5＝45°,∠6＝45°．

(4)由此得,故,因此五边形周长为

16．可拼成如下16种凸多边形．

(第16题)

17．把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边．于是,当将原多边形分割成4个小多边形,最多可以增加4×3＝12条边;当将原多边形分割成8个小多边形,最少可以增加2×7＝14条边．所以分割后的多边形的个数是5,6,7中的一个．设原多边形的边数是n,分割成边数为a1,a2,…,am的m个多边形,则m个多边形的总边数为a1＋a2＋…＋am．由题意,有a1＋a2＋…＋am＝n＋13,180(a1－2)＋180(a2－2)＋…＋180(am－2)＝1．3·180(n－2),得20m＝156－3n＝3(52－n)．所以m是3的倍数,于是m＝6,n＝12．故原来的多边形是12边形,把原来的多边形分割成了6个多边形．

18．∠A4,∠A5,…,∠An的外角和为360°－255°＝105°,

于是∠A4＋∠A5＋…＋∠An＝(n－3)180°－105°＝180°n－645°,

又∠A4＋∠A5＋…＋∠An＝15°(k1＋k2＋…＋kn－3)(ki为整数,i＝1,2,…,n－3),

得180°n－645°＝15°(k1＋k2＋…＋kn－3),即12n－43＝k1＋k2＋…＋kn－3．

由15°ki＜180°,得ki＜12,ki最大只能取11,

∴12n－43≤11(n－3),得n≤10．

故n的最大值为10．

19．假设凸n边形中有k个内角等于150°．则不等于150°的内角有(n－k)个．

(1)若k＝n,由n×150°＝(n－2)×180°,得n＝12．于是,正十二边形的12个内角均为150°．

(2)若k＜n,且n≥13,由k×150°＋(n－k)×180°＞(n－2)×180°,可得k＜12,即k≤11．

当k＝11时,存在凸n边形,其中的11个内角为150°,其余(n－k)个内角均为

(3)若k＜n,且8≤n≤11,当k＝n－1时,存在凸n边形,其中的n－1个内角为150°,另一个内角为

α＝(n－2)×180°－(n－1)×150°＝(n－7)×30°∈[30°,120°]．

(4)若k＜n,且3≤n≤7,由(3)可知k≤n－2,当k＝n－2时,存在凸n边形,其中n－2个内角为150°,另两个内角均为(n－2)×15°．

综上,当n＝12时,k的最大值为12;

当n≥13时,k的最大值为11;

当8≤n≤11时,k的最大值为n－1;

当3≤n≤7时,k的最大值为n－2．