全等三角形和相似三角形的研究是重要的,因为它与运动、相似这些几何变换密切相关。但作为解题的基本工具,全等三角形与相似三角形的方法就暴露出明显的不足。我们着眼于那些任何几何图形中都会出现的三角形对,这就是“共边三角形”和“共角三角形”。两个三角形如果有一条公共边,我们就说这两个三角形是共边三角形。这样有一组对应角相等或互补的一对三角形,叫做共角三角形。......
2023-10-17
将点、线、面体不同形态的基本图形加以组合,便构成一个新的图形.基本图形有规律地、渐渐地演变,又构成新的图形.埃舍尔创作的《天与水》运用异形渐变的构成方法,使天上的飞鸟和水中的游鱼有机结合在一起,埃舍尔是荷兰版画家,他把自己称为一个“图形艺术家”.
知能概述
三角形是最简单、最基本的几何图形,是研究其他复杂图形的基础.
边与角是三角形的基本元素,与边与角相关的知识有:三角形三边关系定理、三角形内角和定理及推论,它们在相关计算、图形计数等方面有广泛的应用.
解与三角形的边与角有关的问题时,常常用到数形结合及分类讨论法,即用方程、不等式解边与角的计算及简单推理题,按边或角对三角形进行分类讨论.
问题解决
例1 如图,∠CAD和∠CBD的平分线相交于点P,设∠CAD,∠CBD,∠C,∠D的度数依次为a,b,c,d,用仅含有2个字母的代数式表示∠P的度数_________.
(江苏省竞赛题)
解题思路 运用对顶三角形的性质,可得到含∠P,a,b,c,d的等式.
几何学会给你带来许多幸福的时刻,几何学不仅是发展智慧的手段,而且也是医治心灵和肉体的良药.
——依·沙雷金
质数角度的直角三角形
罗巴切夫斯基(1792—1856),俄国数学家,他一生的重要贡献是创立了“非欧几里得几何”,他曾思考过下面的问题:
有无锐角角度均为质数的直角三角形?若有,有多少个?进一步问:三个角度均为质数的不等边三角形存在吗?这样的等腰三角形存在吗?
例2 已知△ABC的三个内角的比是m∶(m+1)∶(m+2),其中m是大于1的正整数,那么△ABC是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
(“希望杯”邀请赛试题)
解题思路 设∠A=mt,则∠B=(m+1)t,∠C=(m+2)t(t>0),比较∠A+∠B与∠C的大小.
例3 若三角形一个角与90°相差不大于15°,称之为几乎直角三角形;若三角形两个角相差不大于15°,称之为几乎等腰三角形.任一锐角三角形是否要么几乎直角要么几乎等腰?
(环球城市数学竞赛试题)
解题思路 从肯定或否定切入,解题的关键是建立或导出与定义相关的不等式.
例4 (1)已知三角形的三边a,b,c的长都是整数,且a≤b<c,b=7,问:这样的三角形有多少个?
(湖北省武汉市竞赛题)
(2)周长为30,各边长互不相等且都是整数的三角形共有多少个?
(河南省竞赛题)
解题思路 对于(2),不妨设三角形三边为a,b,c,且a<b<c,由三角形三边关系定理及题设条件可确定c的取值范围,以此作为解题的突破口.
确立三角形个数是与三角形三边关系相关的一类重要问题,解题的基本方法有:
(1)已知边长(次长边或最长边),通过穷举确定三角形个数;
(2)已知周长确定三角形个数,解题的关键是先求出最长边的取值范围,可以证明:三角形的最长边介于周长的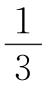 和
和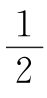 之间.
之间.
三角形是一个从简单情形出发,逐步走向深刻的最具典型性的数学研究对象,人们一定是掌握了某些三角学知识,才能建造起宏伟的金字塔,让它历经千年风雨依然威严耸立.
例5 在三角形纸片内有2008个点,连同三角形纸片的3个顶点,共有2011个点,在这些点中,没有三点在一条直线上.问:以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形?
(天津市竞赛题)
解法1 我们不妨先退一步,考察三角形内有一个点,两个点,三个点…的简单情形,有下表所示的关系:
不难发现,三角形内有一个点时,连线可得到3个小三角形,以后每增加一个点,这个点必落在已连好的某一个小三角形内,它与该三角形的三个顶点可得到三个小三角形,从而增加了两个小三角形,于是可以推出,当三角形内有2008个点时,连接可得到小三角形的个数为:3+2×(2008-1)=4017(个).
解法2 整体核算法.设连线后把原三角形分割成n个小三角形,则它们的内角和为180°·n,又因为原三角形内每一个点为小三角形顶点时,能为小三角形提供360°的内角,2008个点共提供内角2008×360°,于是得方程180n=360×2008+180,解得n=4017,即这2008个点能将原三角形纸片分割成4017个小三角形.
例6 (1)用长度相等的100根火柴杆,摆放成一个三角形,使最大边的长度是最小边长度的3倍,求满足此条件的每个三角形的各边所用火柴杆的根数.
(山西省太原市竞赛题)
(2)现有长为150cm的铁丝,要截成n(n>2)小段,每段的长为不小于1cm的整数.如果其中任意3小段都不能拼成三角形,试求n的最大值,此时有几种方法将该铁丝截成满足条件的n段?
(江苏省竞赛题)
分析与解 对于(1),设三角形各边需用火柴杆数目分别为x,y,3x,综合运用题设条件及三角形三边的关系等知识,建立含等式、不等式的混合组,这是解本例的突破口;对于(2),因n段之和为定值150cm,故欲n尽可能的大,必须每段的长度尽可能的小,这样依题意可构造一个数列.
(1)依题意,有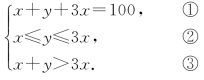
由①,②得![]() ≤x≤20,由③得x<
≤x≤20,由③得x<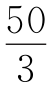 ,因x为正整数,故x=15或16.所以,满足条件的三角形有两组,需用火柴杆数目分别为15,40,45或16,36,48.
,因x为正整数,故x=15或16.所以,满足条件的三角形有两组,需用火柴杆数目分别为15,40,45或16,36,48.
华罗庚曾说:“善于‘退’,足够地‘退’,‘退’到原始而不失去重要的地方,是学好数学的一个诀窍.”
对于例5,如果用剪刀沿着这些小三角形的公共边剪开来(一条公共边算一刀),那么要剪成这些小三角形要剪几刀?
解与三角形的边与角相关的问题时,常常要根据等式和不等式的性质,用不等值替换,通过放缩(放大求下界、缩小求上界)确定三角形的边或角的范围.
(2)这些小段的长度只可能分别是1,1,2,3,5,8,13,21,34,55,89…但1+1+2+…+34+55=143<150,1+1+2+…+34+55+89=232>150,故n的最大值为10,共有以下7种方式:(1,1,2,3,5,8,13,21,34,62),(1,1,2,3,5,8,13,21,35,61),(1,1,2,3,5,8,13,21,36,60),(1,1,2,3,5,8,13,21,37,59),(1,1,2,3,5,8,13,22,35,60),(1,1,2,3,5,8,13,22,36,59),(1,1,2,3,5,8,14,22,36,58).
规形探究
例7 (1)如图①,凹四边形ABDC形似圆规,这样的凹四边形称为“规形”,易证∠BDC=∠A+∠B+∠C.
(2)如图②,在凹四边形ABDC中,已知∠ABD与∠ACD的平分线交于点E.求证:∠E=![]() .
.
拓展
“规形”有四个内角,任取两个内角的平分线,有六种组合情形,于是,可提出下列问题:
(1)如图③,若∠ABD,∠BAC的平分线交于点E,则∠C,∠D与∠E之间有怎样的数量关系?
(2)如图④,若∠BAC,∠BDC的平分线交于点E,则∠B,∠C与∠E之间有怎样的数量关系?
解题思路 当角平分线与三角形相遇可生成内涵上有关联性、解法上有共通性的组图.引入字母,设而不求,充分体现代数化方法在解与角平分线相关问题时的广泛应用.
角是平面图形的基本元素,突破角的关系是解平面几何问题的关键,你熟悉下列图形中角的关系吗?
1.如图,在△ABC中,O是△ABC三条角平分线的交点,若∠AOB∶∠BOC∶∠AOC=4∶5∶6,则∠ABC=________度.
(“希望杯”邀请赛试题)
2.如图,加油站A和商店B在马路MN的同一侧,A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走.问:当P到A的距离与P到B的距离之差最大时,这个差等于_________米.
(“华罗庚金杯”少年数学邀请赛试题)
(第1题)
(第2题)
(第5题)
3.将长度为25cm的细铁丝折成边长都是质数(单位:厘米)的三角形,若这样的三角形的三边的长分别是a,b,c,且满足a≤b≤c,则(a,b,c)有_________组解,所构成的三角形都是_________三角形.
(“希望杯”邀请赛试题)
4.已知△ABC的三边长分别为a,b,c,有以下四个命题:
(1)以![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
(2)以a2,b2,c2为边长的三角形一定存在;
(3)以![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
(4)以|a-b|+1,|b-c|+1,|c-a|+1为边长的三角形一定存在.其中,正确的命题是_________(填序号).
(北京大学博雅计划数学测试题)
5.三角形内角平分线的交点称为内心.如图,D是△ABC的内心,E是△ABD的内心,F是△BDE的内心.若∠BFE的度数为整数,则∠BFE至少为_________度.
(上海市竞赛题)
6.长为![]() 的三条线段可以构成一个三角形,则自然数n=_________.
的三条线段可以构成一个三角形,则自然数n=_________.
(世界数学团体锦标赛试题)
7.如图,∠ABD与∠ACD的角平分线交于点P.若∠A=50°,∠D=10°,则∠P的度数为( ).
A.15° B.20°
C.25° D.30°
(第7题)
8.已知△ABC的三个内角∠A,∠B,∠C满足3∠A>5∠B,3∠C≤2∠B,则这个三角形是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
(“希望杯”邀请赛试题)
9.如图,将纸片△ABC沿着DE折叠展平,则( ).
A.∠A=∠1+∠2
B.∠A=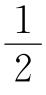 (∠1+∠2)
(∠1+∠2)
C.∠A=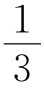 (∠1+∠2)
(∠1+∠2)
D.∠A=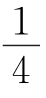 (∠1+∠2)
(∠1+∠2)
(第9题)
(北京市竞赛题)
10.已知一个三角形的三条边长均为正整数,若其中仅有一条边长为5,且它又不是最短边,则满足条件的三角形有( ).
A.4个 B.6个 C.8个 D.10个
(天津市竞赛题)
11.7条长度均为整数的线段a1,a2,…,a7满足a1<a2<…<a7,且这7条线段中的任意三条线段都不能构成三角形,若a1=1,a7=21,则a6=( ).
A.18 B.13 C.8 D.5
(浙江省竞赛题)
12.边长为整数,周长为20的三角形共有( )个.
A.4 B.6 C.8 D.12
(江西省南昌市竞赛题)
13.不等边△ABC的两条高长度分别为4和12,若第三条高的长也是整数,试求它的长.
(美国数学邀请赛试题)
14.有长度分别为1,2,3,4,5,6,7,8,9(单位:cm)的细木棒各一根,利用它们(允许连接加长但不允许折断)能够围成多少种周长不同的等边三角形?
(江苏省竞赛题)
15.如图,在△ABC中,已知三条内角平分线AD,BE,CF相交于I,IH⊥BC,求证:∠BID=∠HIC.
(湖北省武汉市竞赛题)
(第15题)
(第16题)
16.如图,已知射线Ox⊥Oy,A,B为Ox,Oy上两动点,∠A平分线与∠B的外角平分线交于C,试问:∠C的度数是否随A,B运动而发生变化?若变化,请说明理由;若不变化,求出∠C的值.
(四川省竞赛题)
17.从1,2,…,2004中任选k个数,使所选的k个数中,一定可以找到能构成三角形边长的3个数(这里要求三角形三边长互不相等).试问:满足条件的k的最小值是多少?
(山东省竞赛题)
18.若三角形的三条边长a,b,c为整数,且一边上的高恰为另两条边上的高之和,则称这样的三角形为“玲珑三角形”.证明:
(1)存在玲珑三角形;
(2)玲珑三角形中,a2+b2+c2为完全平方数.
(北京市竞赛题)
19.如图①,点D,点E分别在△ABC边AB,AC上,∠CBD=∠CDB,DE∥BC,∠CDE的平分线交AC于F点.
(1)求证:∠DBF+∠DFB=90°;
(2)如图②,如果∠ACD的平分线与AB交于G点,∠BGC=50°,求∠DEC的度数;
(3)如图③,如果H点是BC边上的一个动点(不与B,C重合),AH交DC于M点,∠CAH的平分线AI交DF于N点.当H点在BC上运动时,![]() 的值是否发生变化?如果变化,说明理由;如果不变,试求出其值.
的值是否发生变化?如果变化,说明理由;如果不变,试求出其值.
(第19题)
20.在边长都是正整数的三角形中,周长是2009的三角形与周长是2012的三角形哪一种的个数多?说明理由.
(北京市竞赛题)
21.给定n(n>4)条线段,已知用其中任意的n-1条线段均可作成一个n-1边形.求证:可用其中的某三条线段为边作成一个三角形.
(俄罗斯圣彼得堡市竞赛题)
22.是否存在这样的三角形,其三边之长x,y,z满足x3+y3+z3=(x+y)(y+z)(z+x)?
(俄罗斯数学竞赛题)
例1 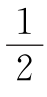 (c+d) 在△ADE和△EPB中有:
(c+d) 在△ADE和△EPB中有: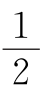 a+d=∠P+
a+d=∠P+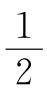 b,在△BCF和△PAF中有:
b,在△BCF和△PAF中有: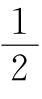 b+c=∠P+
b+c=∠P+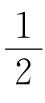 a,两式相加,得c+d=2∠P,∠P=
a,两式相加,得c+d=2∠P,∠P=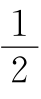 (c+d).
(c+d).
例2 A ∠A+∠B=(2m+1)t=(m+2)t+(m-1)t.因m>1,t>0,故∠A+∠B>∠C,∠C<90°,∠C是△ABC最大的角.
例3 是.设三个角A≥B≥C,若不是几乎等腰,则A-B,B-C>15°,A-C>30°,由180°=A+B+C<A+A-15°+A-30°=3A-45°,A>75°,|A-90°|<15°,故是几乎直角.
例4 (1)分a=1,2,…,7情形讨论,又a+b>c,列表如右:
(2)不妨设a<b<c,则
得10<c<15.
因c为整数,故c=11,12,13,14.
当c=11时,b=10,a=9.当c=12时,b=11,a=7;b=10,a=8.当c=13时,b=12,a=5;b=11,a=6;b=10,a=7;b=9,a=8.当c=14时,b=13,a=3;b=12,a=4;b=11,a=5;b=10,a=6;b=9,a=7.
例7 (1)略
(2)题图②可分解为两个“规形”,
∵BE,CE分别平分∠ABD,∠ACD,
∴可设∠ABE=∠DBE=x,∠ACE=∠DCE=y.
由(1)得∠E=∠A+x+y, ①
∠D=∠E+x+y, ②
②-①得∠D-∠E=∠E-∠A,
∴∠E=![]()
拓展:略
1.108 2.7 |PA-PB|≤AB,当A,B,P在一条直线上时,等号成立.
3.两 等腰 最长边介于周长的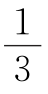 和
和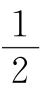 之间,故最长边可取整数12,11,10,9,又三边长都是质数,则最长边为11,另两边的和为14.其中符合条件的有11+11+3=25,7+7+11=25.
之间,故最长边可取整数12,11,10,9,又三边长都是质数,则最长边为11,另两边的和为14.其中符合条件的有11+11+3=25,7+7+11=25.
4.(1)(3)(4) 对于(3)(4),设a≥b≥c,则 ,|c-a|+1分别大于或等于其余两边,只需说明
,|c-a|+1分别大于或等于其余两边,只需说明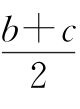 +
+![]() ,|a-b|+1+|b-c|+1>|c-a|+1.
,|a-b|+1+|b-c|+1>|c-a|+1.
9.B
10.D 当5是最长边时,有(2,4,5),(4,4,5),(3,4,5),(3,3,5);当5是次长边时,有(2,5,6),(3,5,6),(3,5,7),(4,5,6),(4,5,7),(4,5,8),共10个.
11.B 只有当a2=2,a3=a1+a2=3,a4=a2+a3=5,a5=a3+a4=8,a6=a4+a5=13时,7条线段中的任意三条都不能构成三角形.
12.C 参见例4.
13.设长度为4和12的高分别是边a,b上的,边c上的高为h,△ABC的面积为S,则a=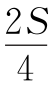 ,b=
,b=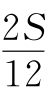 ,c=
,c=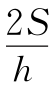 ,由
,由![]() ,得3<h<6,故h=5.
,得3<h<6,故h=5.
14.因所有线段的和为45,故最大的等边三角形边长为15.依据周长列表如下:
15.设∠CAB=2α,∠ABC=2β,∠BCA=2γ,则α+β+γ=90°.因为∠BID=α+β,∠HIC=90°-γ=α+β,故∠BID=∠HIC.
16.不变化,∠C=90°-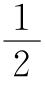 ∠AOB=45°为一定值.
∠AOB=45°为一定值.
17.这一问题等价于:在1,2,…,2004中选k-1个数,使其中任何3个数都不能成为一个三角形三边(互不相等)的长.试问:满足这一条件的k的最大值是多少?
符合上述条件的数组中,当k=4时,最小的3个数就是1,2,3,由此可不断扩大该数组:只要加入的数大于或等于已得数组中最大的两个数之和.所以,为使k达到最大,可选加入之数等于已得数组中最大的两数之和,于是得到:1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597…①共16个数,对符合上述条件的任一数组a1,a2,…,an,显然,总有ai大于或等于①中的第i个数,所以,n≤16≤k-1,从而,k的最小值为17.
18.(1)如:三边长为6,10,15的三角形为一个玲珑三角形.
(2)设玲珑三角形的三边长为整数a,b,c,面积为S,三条边上的高分别为ha,hb,hc.
不妨设ha=hb+hc.
由关系式aha=bhb=chc=2S,得
⇒bc-(ac+ab)=0
⇒a2+b2+c2
=a2+b2+c2+2[bc-(ac+ab)]
=(b+c-a)2.
从而,a2+b2+c2为完全平方数.
19.(1)略 (2)∠DEC=100° (3)原式的值不变,为2.
20.两种三角形的个数相等.
设正整数k≥n≥m是周长为2009的三角形边长.则正整数k+1,n+1,m+1是周长为2012的三角形边长.这样的三角形存在,因为由m+n>k⇒(m+1)+(n+1)>(k+1),即每个周长为2009的三角形都有周长为2012的三角形与之对应.
下面证明:每个周长为2012的三角形都有周长为2009的三角形与之对应.
设K≥N≥M是周长为2012的三角形边长.
(1)其所有边长大于1.
事实上,三角形的每条边大于另两边的差,若某边长为1,则另外两条边应当是彼此相等的,并且在这种情形下三角形的周长是奇数.
(2)M+N>K.
由此得(M-1)+(N-1)≥(K-1).
当等式成立时,得M+N+K=2K+1(奇数),它等于2012,这意味着数M-1,N-1,K-1中两个较小数的和大于第三个,且这些数是某个三角形的三边长.
故周长是2009的三角形与周长是2012的三角形的个数一样多.
21.设a1,a2,a3,…,an-1,an表示题设的n条线段,不妨设a1≤a2≤a3≤…≤an-1≤an,
假设以所给的n条线段中任三条为边均不能构成三角形,则有
a3≥a1+a2,a4≥a2+a3,a5≥a3+a4,…,an≥an-2+an-1,
相加得 an≥an-2+an-3+an-4+…+a3+2a2+a1,
更有 an≥an-2+an-3+an-4+…+a3+a2+a1,
这表明,以an,an-2,an-3,an-4,…,a3,a2,a1这n-1条线段为边不能构成一个n-1边形,与已知矛盾!因此,可用其中的某三条线段为边作成一个三角形.
22.不存在
假设存在这样的三角形,不妨设x≥y≥z,则y+z>x.
∴(x+y)(z+x)(y+z)>(x+y)(z+x)x
=x3+x2y+x2z+xyz
>x3+x2y+x2z
≥x3+y3+z3.
这与题设矛盾.
有关精英数学大视野·七年级2020的文章

全等三角形和相似三角形的研究是重要的,因为它与运动、相似这些几何变换密切相关。但作为解题的基本工具,全等三角形与相似三角形的方法就暴露出明显的不足。我们着眼于那些任何几何图形中都会出现的三角形对,这就是“共边三角形”和“共角三角形”。两个三角形如果有一条公共边,我们就说这两个三角形是共边三角形。这样有一组对应角相等或互补的一对三角形,叫做共角三角形。......
2023-10-17

在数学上,“包络”是指一系列的直线或曲线包围出另一个形状的情形,如左图中若干条直线组成了心脏线、抛物线.20世纪初,西方的数学书上讲述了用直线画曲线的各种画法,当时形成了“数学刺绣”的时尚.知能概述若把8个物体放入7个抽屉,则一定有一个抽屉放了2个或2个以上的物体;若把8个物体放入2个抽屉,则一定有一个抽屉放了4个或4个以上的物体;若把8个物体放入3个抽屉,则一定有一个抽屉放了3个或3个以上的物体......
2023-08-13

璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西.”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意.知能概述图形有具体的,有抽象的;有平面的,有立体的.它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录.立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方......
2023-08-13

+|x-1997|的最小值.分析与解由于x具有任意性、无限性,所以通过逐个求出代数式的值来解题显然较难,不妨借助数轴,从绝对值的几何意义入手.从数轴上看,求|x-1|+|x-2|+|x-3|+…+|x-1997|的最小值,即在数轴上找出表示x的点,使它到表示数1,2,3,…+|x-an|值最小.质点运动运动与静止是哲学中的一对矛盾体,运动中蕴含了事物的相对静止,而在静止中又蕴含了事物的绝对运动.质点在数轴上运动,使点表示的有理数、线......
2023-08-13

命题41 若一个平行四边形和一个三角形既同底又在两平行线之间,则平行四边形面积是三角形的2 倍。图3.12.7《几何原本》卷一命题43若AC 为ABCD 的对角线,则其所谓平行四边形补形为BGKE 和KFDH。利用三角形全等可以证明之。图3.12.8《几何原本》卷一命题44若已知线段为AB,直线角为D,三角形为C,求作以AB为一边、某底角等于∠D、面积等于三角形C 的平行四边形。连接BD,则问题就转化为作两个平行四边形,其面积分别等于两个三角形的面积。......
2023-11-23

图一图二活动目标1.感知三角形的多种变式,体验图形的翻转与变化。活动准备不同形状三角形共18个;城堡拼图底板2幅(见图四);磁性板3块(见图五)。活动难点运用翻转、旋转变化等方法变换三角形,解决游戏中的问题。活动过程一、游戏“找朋友”1.认识不同变式的三角形提问:看看这些三角形都相同吗?虽然它们长得不一样,但它们都有三条边、三个角,都是三角形。......
2023-08-15

陈省身认为最重要的定理是“三角形内角和定理”与“勾股定理”。我们熟知的“三角形内角和定理”仅在平面上成立,而一般曲面上的三角形其内角和就不是常数了。高斯于1827 年证明了曲面上的三角形内角和公式,后法国数学家博内推广了该公式。1944 年陈省身完成了高斯-博内公式的简单内蕴证明,攻克了“几何学中极其重要和困难的问题”,该论文被誉为数学史上划时代的杰作。......
2023-11-23
相关推荐