相交线与平行线的数学知识大揭秘

利玛窦与徐光启

明代徐光启与意大利传教士利玛窦合作,翻译出版了欧几里得的《几何原本》,西方数学开始传入中国．左图即为利玛窦与徐光启合影．徐光启评价该书说:“此书有四不必:不必疑,不必揣,不必试,不必改．有四不可得:欲脱之不可得,欲驳之不可得,欲减之不可得,欲前后置之不可得．”

知能概述

相交或平行是同一平面内两条直线的基本位置关系．

当两条直线相交或分别与第三条直线相交,就产生对顶角、同位角、内错角、同旁内角等位置关系角,进一步丰富了角的知识,它们在角的计算与证明中有广泛的应用．

与平行线相关的问题一般都是平行线判定与性质的综合运用,有以下两方面的应用:角的计算与证明;两条直线位置关系的确定．

问题解决

例1　(1)O为平面上一点,过O在这个平面上引2005条不同的直线l1,l2,l3,…,l2005,则可形成_________对以O为顶点的对顶角．

(山东省聊城市竞赛题)

(2)若平面上4条直线两两相交,且无三线共点,则一共有_________对同旁内角．

(江苏省竞赛题)

解题思路　对于(1),从简单情形出发,利用递推关系;对于(2),4条直线两两相交,每两个交点之间就有一条线段,而每条线段的两侧各有一对同旁内角,于是将问题转化为确定线段的条数．

几何学的光荣,在于它从很少几条独立自主的原则出发,而得以完成如此之多的工作．

——牛顿

交点几何

平面上有5条不同的直线,这5条直线共形成n个交点,则n有多少个不同的数值?

例2　如图,两直线AB,CD平行,则∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝(　)．

A．630°　B．720°

C．800°　D．900°

(“希望杯”邀请赛试题)

解题思路　分别过E,F,G,H作AB,CD的平行线,运用同旁内角互补求解．

例3　如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠C,∠AEC之间具有怎样的关系?并说明理由．

解题思路　这是一道结论开放的探究性问题,由于E点位置的不确定性,可引起对E点不同位置的分类讨论(如夹在AB,CD之间或之外、内折或外折等),这是解本例的关键．

例4　如图,已知AF∥CD,∠A＝∠D,∠B＝∠E,求证:BC∥EF．

解题思路　怎样利用条件AF∥CD?如何证明BC∥EF?需作辅助线,对内连线或向外补形可得到不同的证法．

例3的问题提出与解决涉及由特殊到一般、运动变化、归纳类比的思想方法,充分展示了一题多变的魅力．过折点作平行线是解这类问题的基本方法．

当从已知条件无法直接推得结论时,我们可以在图中添出新的线,为几何图形性质的运用创造条件,像这样添置的线叫辅助线．辅助线在解题中起着沟通已知与未知、化分散为集中等作用．

例5　平面上有6条两两不平行的直线,试证:在所有的交角中,至少有一个角小于31°．

(莫斯科市竞赛题)

分析与解　把平面上的直线平行移动,则移动后的直线所成的角与移动前的直线所成的角是相等的,这样,我们就可将所有的直线移动后,使它们相交于同一点．此时,情况就相对简单得多．

在平面上任取一点O,过O点分别作这6条直线的平行线l′1,l′2,l′3,l′4,l′5,l′6,则由平行线的特性,知l′1,l′2,l′3,l′4,l′5,l′6之间互成的角与原来的6条直线l1,l2,l3,l4,l5,l6之间互成的角相等．

现在我们考虑l′1,l′2,…,l′6的情况．我们只考察l′1与l′2,l′2与l′3,…,l′5与l′6,l′6与l′1所成的角,由图不难发现这6个角成一个平角,即这6个角的和为180°．

假设这6个角没有一个小于31°,则这6个角都大于或等于31°,从而这6个角的和至少为31°×6＝186°,这是不可能的．所以,这6个角中至少有一个小于31°,不妨设l′1与l′2所成的角小于31°,则原来的直线l1与l2所成的角也必小于31°．

例6　(1)请你在平面上画出6条直线(没有3条共点),使得它们中的每条直线都恰与另3条直线相交,并简单说明画法．

(2)能否在平面上画出7条直线(任意3条都不共点),使得它们中的每条直线都恰与另3条直线相交?如果能,请画出一例;如果不能,请简述理由．

(“希望杯”邀请赛试题)

解(1)如图,在平面上作两组平行直线,m1∥m2∥m3,n1∥n2∥n3．由于彼此平行的直线不相交,所以图中每条直线都恰与另3条直线相交．

(2)在平面上不能画出没有3线共点的7条直线,使得其中每条直线都恰与另3条直线相交．理由如下:

假设平面上可以画出7条直线,其中每一条都恰与其他3条相交,因为两直线相交只有一个交点,又没有3条直线共点,所以每条直线上恰有与另3条直线交得的3个不同的交点．

平行线的本质在于传递角．

过点恰当地作平行线,是现阶段常用辅助线,这是为平行线性质或判定的运用创造了条件;而恰当地平移直线,能把分散的角加以集中．

北大一学生在听了数学素质课后,写下如下的体会:

所有直线表眷恋,

前后延伸情无限．

所有交叉表歧路,

人生处处有考验．

我们按直线去计数这些交点,共有3×7＝21个交点,但每个交点分属两条直线,被重复计数一次,所以这7条直线的交点总数为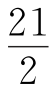个．因为交点个数应为整数,矛盾．

所以,满足题设条件的7条直线是画不出来的．

基本图形分析法

平面图形是平面几何的研究对象,复杂的图形是由一个或者若干个最简单、最基本的图形复合而成,发现这些基本图形也就找到了解决问题的关键所在．

所谓基本图形是指组成一个图形中最基本却又具有特定性质、能彰显应用条件和应用方法的图形;基本图形是图形化的公式,是结论化的图形．

平行线的折线连接,有下面基本形式:

了解相关结论、解决问题的方法是解相关问题的关键．

例7　已知直线AB∥CD．

(1)如图①,若GN平分∠CNE,FM平分∠AMG,F,M,E在同一条直线上,且∠G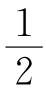＋∠E＝60°,求∠AMG的度数;

(2)如图②,若直线BM平分∠ABE,直线DN平分∠CDE,BM,DN相交于点F,求∠F∶∠E的值．

解题思路　过折点作平行线是解决问题的关键,而恰当地引入字母代数化,能使解题过程清晰明了．

基本图形常见表现形式为:

(1)与概念、公理、定理推论所对应的图形;

(2)重要结论对应的图形;

(3)具有典型性的例题、习题所对应的图形．

埃舍尔对平面镶嵌图案非常感兴趣．如图,鸟和鱼毫无间隙地镶嵌起来,令人赏心悦目．仔细一看,如此复杂的镶嵌只是由一只鸟和一条鱼通过平移而生成．

1．如图,已知AB∥CD,BC∥DE,若∠A＝20°,∠C＝120°,则∠AED的度数是_________．

(浙江省金华市中考题)

(第1题)

(第2题)

(第3题)

2．如图,若AB∥FE,BC⊥ED,∠ABC与∠DEF的角平分线交于点G,则∠BGE的度数是_________．

(“希望杯”邀请赛试题)

3．如图是一块电脑主板模型,每一个转角处都是直角,其数据如图所示(单位:cm),则该主板的周长是________cm．

(重庆市竞赛题)

4．已知∠A的两条边和∠B的两条边分别平行,且∠A比∠B的3倍少20°,则∠B＝________．

(北京市“迎春杯”竞赛题)

5．如图,已知平行直线AB,CD与相交直线EF,GH相交,则图中的同旁内角有________对．

(全国初中数学联赛题)

(第5题)

(第6题)

(第7题)

6．如图,∠AOB的一边OA为平面镜,∠AOB＝37°36′,在OB上有一点E,从点E射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是(　)．

A．75°36′　B．75°12′　C．74°36′　D．74°12′

(山东省枣庄市中考题)

7．如图,若AB∥CD,则∠1＋∠3－∠2的度数等于(　)．

A．90°　B．120°　C．150°　D．180°

(北京市竞赛题)

8．某人在练车场上练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则这两次拐弯的角度可能是(　)．

A．第一次向左拐40°,第二次向右拐40°

B．第一次向右拐50°,第二次向左拐130°

C．第一次向右拐70°,第二次向左拐110°

D．第一次向左拐70°,第二次向左拐110°

(“希望杯”竞赛题)

9．如图,若K∥L,∠4－∠3＝∠3－∠2＝∠2－∠1＝d°＞0,其中∠3＜90°,∠1＝50°,则∠4最大可能的整数值是(　)．

A．107　B．108　C．109　D．110

(北京市竞赛题)

(第9题)

(第10题)

(第12题)

10．如图,将Rt△ABC沿着点B到点C的方向平移到△DEF的位置,AB＝10,DO＝4,平移距离为6．则阴影部分的面积为(　)．

A．48　B．30　C．38　D．50

(广东省中山市中考题)

11．平面上有10条直线,无任何三条交于一点．欲使它们出现31个交点,怎样安排才能办到?(只要求画出符合条件的10条直线)

(吉林省竞赛题)

12．如图,已知CD∥EF,∠1＋∠2＝∠ABC,求证:AB∥GF．

(重庆市竞赛题)

13．已知AB∥CD,点P是直线AB,CD之间一动点．

(1)如图①,求证:∠A＋∠APC＋∠C＝360°;

(2)如图②,若PQ平分∠APC,CQ平分∠PCD,求证:∠A＝2∠PQC;

(3)如图③,若∠A＝144°,∠QPC＝3∠APQ,∠QCP＝3∠QCD,求∠PQC的度数．

(第13题)

14．已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F．

(第14题)

(1)如图①,若∠E＝80°,求∠BFD的度数;

(2)如图②,已知∠ABM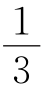＝∠ABF,∠CDM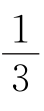＝∠CDF,写出∠M和∠E之间的数量关系并证明你的结论;

(3)若∠ABM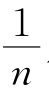＝∠ ABF,∠CDM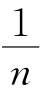＝∠CDF,设∠E＝m°,直接用含有n,m°的代数式表示∠M＝_________．

15．平面上有5条直线,其中任意两条都不平行,那么在这5条直线两两相交所成的角中,至少有一个角不超过36°,请说明理由．

(“华罗庚金杯”少年数学邀请赛试题)

16．两条直线相交,四个交角中的一个锐角(或一个直角)称为这两条直线的“夹角”(如图),如果在平面上画L条直线,要求它们两两相交,并且“夹角”只能是15°,30°,45°,60°,75°,90°之一,问:

(1)L的最大值是多少?

(2)当L取最大值时,问所有的“夹角”的和是多少?

(第16题)

(“华罗庚金杯”少年数学邀请赛试题)

17．已知五个城市两两相连所得的10条道路中,至少有一个交叉路口(如图①),又已知三个村庄和三个城市相连所需的9条道路中,至少有一个交叉路口(如图②)．利用上述结论,用15条道路把6个城市两两相连,至少会产生多少个交叉路口?

(第17题)

(青少年数学国际城市邀请赛试题)

18．平面上画11条水平线段和11条竖直线段．求证:不可能每条水平线段恰与10条竖直线段相交,而每条竖直线段恰与10条水平线段相交．

(俄罗斯圣彼得堡数学奥林匹克试题)

19．点线的乐章

点与线是构成图形的最基本元素,点动成线,线动成面,面动成体,点与线的运动、组合、变化、数字化,可生成复杂的图形,宛如演奏出气势磅礴的优美乐章．

简单地看,连点得线,线交于点,深入地想,屏幕是如何呈现图像的?计算机是怎样画图的?归根到底是基于点的显示．

(1)平面上有6条直线,共有12个不同的交点,画出它们可能的位置关系(画三种图形)．

(江苏省竞赛题)

(2)平面上n条直线中每条恰与另外的1999条相交,求n的所有可能值．

(环球城市数学奥林匹克试题)

(3)伟大的物理学家牛顿在诸多领域均有跨时代的贡献,提出下面这道名题:

9棵树栽9行,每行栽3棵,如何栽?

(4)英国数学家、逻辑学家道奇森在其童话名著《艾丽丝漫游仙境》中也提出过下面一道植树问题:

10棵树栽5行,每行栽4棵,如何栽?

例1　(1)4018020　设过O点的n条不同直线可形成an对对顶角,n＝2时,a2＝2,n＝3时,a3＝a2＋2×2,n＝4时,a4＝a3＋2×3,…,a2005＝a2004＋2×2004＝2×2004＋2×2003＋…＋2×4＋2×3＋2×2＋2×1＝2005×2004＝4018020．

(2)24　共有12条线段,有2×12＝24对同旁内角．

例2　D　所作的平行线与AB,CD都两两互相平行,所求的角的和构造为5对同旁内角的和,即5×180°＝900°．

例3　如图,可分别得到下列关系(证法同①):

(例2)

①∠AEC＝∠A＋∠C;②∠AEC＋∠A＋∠C＝360°;③∠AEC＝∠C－∠A;

④∠AEC＝∠A－∠C;⑤∠AEC＝∠A－∠C;⑥∠AEC＝∠C－∠A．

例4　如图,连接BE,AD．

∵AF∥CD,∴∠1＝∠2．

又∵∠BAF＝∠CDE,∴∠3＝∠4．

∴AB∥DE,得∠5＝∠6,而∠ABC＝∠FED,

∴∠7＝∠8,故BC∥EF．

(例4)

例7　(1)作GS∥AB,ET∥AB,则GS∥AB∥ET∥CD,设∠CNG＝∠GNE＝x,∠FMA＝∠FMG＝y,∠AMG＝40°．

(2)

1．80°

2．135°　延长BC,ED交于点H,则∠BHE＝90°,过点H作HI∥AB,则HI∥AB∥EF,∠BGE＝360°－90°－(∠ABH＋∠HEF)＝360°－90°－135°＝135°．

3．96

4．10°或50°　5．16

6．B　7．D　8．D

9．C　∠2＝50°＋d,∠3＝50°＋2d,∠4＝50°＋3d,d＜20°,50°＋3d为整数．

10．A　S阴影＝S梯形ABEO．

11．可有多种方案,以下仅供参考．

(第11题)

12．作CK∥FG,延长FG,CD交于H点,则∠H＋∠2＋∠BCK＝180°,因∠1＋∠2＝∠ABC,故∠ABC＋∠BCK＝180°,即CK∥AB,AB∥GF．

13．(1)略

(2)过点Q作MN∥PC,设∠APQ＝∠QPC＝x,∠QCP＝∠QCD＝y,则∠PQC＝180°－x－y,∠A＝360°－2x－2y,故∠A＝2∠PQC．

(3)∠PQC＝18°．

14．(1)140°　(2)∠M＝(3)∠M＝

15．①在平面上任取一点O,过O点作已知的5条直线的平行线l1,l2,l3,l4,l5(右图以3条直线为例,说明作平行线的方法)．

②将以O为中心的圆周分解为10个彼此依次相邻的小角,它们的和为360°,故至少有一个小角不超过36°．

(第15题)

16．(1)如图a,固定平面上一条直线,其他直线与此条固定直线的交角自这条固定直线起逆时针计算,只能是15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°这11种角度之一,所以,平面上最多有12条直线．否则,必有两条直线平行．

(第16题)

(2)如图b,将所有直线做平行移动,使它们交于同一个点,这样的平行移动显然不改变两条直线的“夹角”．不妨设其中一条直线水平,从水平直线开始,逆时针将12条直线分别记为第1条、第2条……第12条直线．

①第2条至第12条直线与第1条直线的“夹角”和是:15＋30＋45＋60＋75＋90＋75＋60＋45＋30＋15＝540(度);

②第3条至第12条直线与第2条直线相交的“夹角”和是:15＋30＋45＋60＋75＋90＋75＋60＋45＋30＝(540－15)(度);

③第4条至第12条直线与第3条直线相交的“夹角”和是:15＋30＋45＋60＋75＋90＋75＋60＋45＝(540－15－30)(度);

……

⑩第11条和第12条直线与第10条直线相交的“夹角”和是:(30＋15)(度);

⑪第12条直线与第11条直线相交的“夹角”和是:15(度);

将②和⑪,③和⑩,④和⑨,⑤和⑧,⑥和⑦配对,得到所有的“夹角”之和是6×540＝3240(度)．

17．如图,至少会有3个交叉路口．

(第17题)

假设最多只有两个交叉路口,可以去掉两条路使其余的路不产生交叉路口,考虑以下两种情况:

(1)去掉的路与同一个城市相连．

考虑其余的5个城市,它们两两相连．但是根据已知条件,至少有一个交叉路口,矛盾．

(2)去掉的两条路不与同一个城市相连．

选取其中一条去掉的路所关联的两个城市,再取一个与去掉的路不相连的城市,称这3个城市为村庄．则这3个村庄和3个城市有路相连．由已知条件,必有一个交叉路口,矛盾．

18．反设题目所述情形出现,则对于每条水平线段,有且只有一条竖直线段不与它相交,将它们配成一对．每条线段(水平或竖直)都属于且只属于一个这样的对．故所有线段划分为11个水平—竖直对．同一对中的两线段不相交,而不同属一对的水平线段与竖直线段相交．

作出所有水平线段所在的直线,设L1,L2分别是其中最上,最下一条(允许L1＝L2)．任取L1上的线段a1和L2上的线段a2(若L1＝L2,应取a1≠a2)．设与它们配对的竖直线段为b1,b2．则其余9条竖直线段应当与a1,a2都相交,即穿越带域L1—L2．设它们依左右次序为b3,b4,…,b11．现在考虑与b4配对的水平线段a4,它位于带域L1—L2中,又与b3,b11都相交,故与b3,b4,…,b11全相交,矛盾．

19．(1)

(第19题)

(2)依平行关系分类,设共有k类,各类的条数为．同类的直线不相交,不同类的均相交．第i类的线与其他类的n－ai条都相交,故由题设条件得到n－a1＝n－a2＝…＝n－ak＝1999．于是a1＝…＝ak＝a,n＝ka,1999＝n－a＝(k－1)a．因为1999是素数,只有两组解(2,1999)和(2000,1)．得出n＝3998或2000．

把树看作点,行抽象成线,问题的实质是探讨点与线的关系,画图、实验、调整．

(3)有不同栽法,如图:

(第19题)

图②表示:9棵树每行栽了3棵,可栽行数的最大值是10．

(4)下列栽法仅供参考．

(第19题)