七年级数学第20讲：线段与角

欧几里得的《几何原本》

给出点、线、面等23个定义,提出5个公式和5个公理,以此作为推理的基础,古希腊数学史上最具影响的是大数学家欧几里得和他的巨著《几何原本》．《几何原本》是由公理法建立起来的数学演绎体系的最早典范,其中不少内容仍为当今人们学习几何的材料．这本书一直以手抄本形式流传了1800多年,直至1482年首次以印刷形式发行．

知能概述

线段与角是构成几何图形的最基本元素,是从现实的相关形象中抽象出来,为现实问题的解决提供有力的工具,使得许多问题的研究可以转化为直观、简明的几何图形的研究．

解线段与角相关问题,常用到中点、角平分线、代数化、枚举与分类讨论等概念与方法．

问题解决

例1　(1)平面内两两相交的6条直线,其交点个数最少为________个,最多为_________个．

(“希望杯”邀请赛试题)

(2)如图,∠BOD＝45°,∠AOE＝90°,那么不大于90°的角有________个,它们的度数之和是_________．

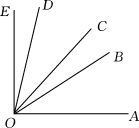
(“希望杯”邀请赛试题)

解题思路　对于(1),画图探求,从简单情形考虑,从特殊情形考虑;对于(2),求它们的度数和,关键是把一些角重组,用∠BOD,∠AOE表示．

几何学中无王者之道．

——欧几里得

植树问题

道奇森,英国数学家、逻辑学家,还是一位童话作家,曾以笔名L．卡洛尔发表了风靡世界的《爱丽丝漫游仙境》,他在这本书中提出下面的问题:

10棵树栽成5列,怎样栽可使每列有4棵树．

例2　(1)如图①,已知B是线段AC上的一点,M是线段AB的中点,N是线段AC的中点,P为NA的中点,Q为MA的中点,则MN∶PQ等于(　)．

A．1　B．2　C．3　D．4

(“五羊杯”邀请赛试题)

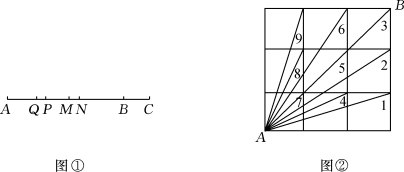
(2)如图②,是一个3×3的正方形,则图中∠1＋∠2＋∠3＋…＋∠9的度数是(　)．

A．270°　B．315°　C．360°　D．405°

(广东省竞赛题)

解题思路　对于(1),利用中点,设法把MN,PQ用含相同线段的代数式表示;对于(2),除∠3＝∠5＝∠7＝45°,其他各角的度数无法求出,故不能顺序求和,关键是对图形进行恰当地处理．

例3　摄制组从A市到B市有一天的路程,计划上午比下午多走100千米到C市吃午饭,由于堵车,中午才赶到一个小镇,只行驶了原计划的三分之一,过了小镇,汽车赶了400千米,傍晚才停下来休息,司机说,再走从C市到这里路程的二分之一就到达目的地了,问A,B两市相距多少千米?

(“华罗庚金杯”少年数学邀请赛试题)

解题思路　条件中只有路程,而没有给出时间与速度,所以应当集中注意于各段路程之间的关系,画线段图分析,借助图形思考．

数学既研究数,也研究形,许多数学问题既可以从代数角度来思考,也可以从形的角度加以解决．

线段图能直观形象地表示数量关系、位置关系或其他意义,恰当地画出线段图,常有助于问题的解决．

“谋定而后动”,解题方法的选择建立在分析的基础上,切忌“慌不择路”,扎进“死胡同”．

例4　如图,A是数轴上表示－30的点,B是数轴上表示10的点,C是数轴上表示18的点．点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒．设三个点运动的时间为t(秒),

(1)当t为何值时,线段AC＝6(单位长度)?

(2)当t≠5时,设线段OA的中点为P,线段OB的中点为M,线段OC的中点为N．求2PM－PN＝2时t的值．

解题思路　把相关点表示的数、相应线段长用t的代数式表示,建立方程．因多个点以不同速度在运动变化中,故注意多种位置关系,全面讨论是解题的关键．

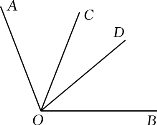
例5　已知∠AOB＝120°(本题中的角均大于0°且小于180°)

(1)如图①,在∠AOB内部作∠COD,若∠AOD＋∠BOC＝160°,求∠COD的度数;

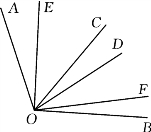
(2)如图②,在∠AOB内部作∠COD,OE在∠AOD内,OF在∠BOC内,且∠DOE＝3∠AOE,∠COF＝3∠BOF,∠EOF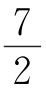＝∠COD,求∠EOF的度数;

(3)射线OI从OA的位置出发绕点O顺时针以每秒6°的速度旋转,旋转时间为t秒(0＜t＜50且t≠30)．射线OM平分∠AOI,射线ON平分∠BOI,射线OP平分∠MON．若∠MOI＝3∠POI,则t＝_________秒．

图①

图②

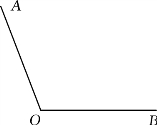
备用图

解题思路　对于(2),引入字母表示角,将问题代数化;对于(3),设旋转n°,随着t的变化,∠IOM、∠POI分别对应着关于n的不同表达式,故注意t的限制、多次画图、分类讨论是解题的关键．

例4通过赋予点的运动,把问题引向深刻．解动态性问题的常用策略是:

(1)动中觅静

即寻找不变量或不变性．

(2)以静制动

即关注特殊状态并建立方程．

(3)以动制动

即建立代数式或关系式．

例6　一条直线上顺次排列着1990个点:P1,P2,…,P1990,已知点Pk是线段Pk－1Pk＋1的k等分点当中最靠近Pk＋1的那个分点(2≤k≤1989),如P5是线段P4P6的5等分点当中最靠近P6的那个分点．如果线段P1P2的长度是1,线段P1989P1990的长度为l．

求证: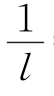＝ 1988·1987·…·3·2．

(浙江省竞赛题)

分析与解　从简单情形入手,寻找线段PkPk＋1与Pk－1Pk的关系．

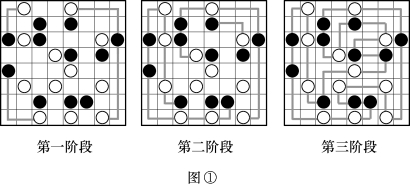
例7　请在图中绘出一条通过每一个小方格一次且不与自身相交的封闭路径,使得路径上的两个相邻的圆圈之间的线段满足下列条件:

(1)若两个圆圈同色,则它们之间由一条直线段相连接;

(2)若两个圆圈异色,则它们之间由相交为直角的两条直线段相连接．

(所绘出的封闭路径必须由水平线段或垂直线段所构成)

(青少年数学国际城市邀请赛试题)

分析与解　可先从位于四个角落的方格都必须是由两条互交为直角的直线段相连接而成来判断出图①中第一阶段的连接方式,接着便可依序判断出第二阶段、第三阶段而完成绘图．

直线段上的n个点至多可将它分成n＋1个部分．

瑞士出生的德国数学家斯坦纳将上述问题稍作推广:

平面上的n条直线至多可将平面分成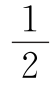(n2＋n＋2)个部分．

你能证明吗?

数学中的严谨推理和一丝不苟的计算,使得每一个数学结论都是牢固的、不可动摇的．关于欧几里得的严密体系,爱因斯坦曾说:“世界第一次目睹了一个逻辑体系的奇迹,这个逻辑体系如此精密地一步一步推进,以至它的每一个命题都是绝对不容置疑的——我这里说的是欧几里得几何。推理的这种可赞叹的胜利,使人类理智获得了为取得以后成就所必需的信心．”

钟表上的角度

我们常常把抽象的时间问题转化为具体的平面几何问题,再根据角度间的等量关系建立方程求解;或运用时针和分针的不同运动速度,转化为行程问题中的追及问题来求解．

例8　在0时到12时之间,钟面上的时针与分针在什么时候成60°的角?试尽可能多地找出答案,又秒针与时针共有几次成60°的角?

解题思路　直觉作答或近似估计,可得到一些答案,而通过方程可使我们找到问题全部的解．

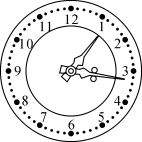
而列方程解答,又有几种不同的解题策略:

(1)分别对两个整点之间的答案列出方程求解;

(2)在上述基础上寻找规律求出全部解;

(3)将问题看成圆周追及问题．设分针的速度为每分钟1个单位长度,则时针的速度为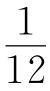．将时针、分针看成两个不同速度的人在环形跑道上同时(从0时开始)同向而行,要求使两者相距10个单位长度所用的时间．

1．平面内有若干条直线,当下列情况时,可将平面最多分成几部分?

(1)有一条直线时,最多可分成2部分;

(2)有两条直线时,最多可分成4部分;

(3)有三条直线时,最多可分成_________部分;

(4)有n条直线时,最多可分成________部分．

(广西壮族自治区竞赛题)

2．从长度为1的线段开始,第一次操作将其三等分,并去掉中间的一段;第二次操作将余下的线段各三等分,并去掉所分线段中间的一段．此后每次操作都按这个规则进行．如图是最初几次操作的示意图．当完成第六次操作时,余下的所有线段的长度之和为_________．

(“希望杯”邀请赛试题)

(第2题)

解钟表上的问题,常用到以下知识:

(1)钟表上相邻两个数字之间有5个小格,每个小格表示1分钟,如与角度联系起来,每小格对应6°;

(2)秒针每分钟转过360°,分针每分钟转过6°,时针每分钟转过0．5°;

(3)画示意图把这类问题看成是行程问题中的追及问题来解决．

为什么说几何是神圣的?因为几何是推理的最具体,同时也是最抽象的形式;几何是许多事物,甚至是全部事物的原型模式,无论那事物是实体的、概念的、数学的、自然的或者建筑的．

平面几何知识不仅是人类支配自身的力量,而且优化了人类自身的发展——人类理性思维的进步．

3．平面上不重合的两点确定1条直线,不同3点最多可确定3条直线．若平面上不同的n个点最多确定21条直线,则n的值为________．

(湖北省黄石市中考题)

4．如图,“回”字形的道路宽为1米,整个“回”字形是一个长16米、宽8米的长方形场地．如果你沿着小路的中间从内部出发走完这条小路,共走________米．

(《美国数学月刊》试题)

5．王明在早晨6点至7点之间外出晨练,出门和回家的时候,时针与分针的夹角都是110°,则王明晨练的时间为_________分钟．

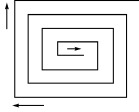
(第4题)

(“希望杯”邀请赛试题)

6．在一个圆形时钟的表面,OA表示秒针,OB表示分针(O为两针的旋转中心)．若现在时间恰好是12点整,则经过_________秒后,△OAB的面积第一次达到最大．

(全国初中数学竞赛题)

7．摇摆不定

已知线段OP＝1,取OP的中点P1,取PP1的中点P2,取P1P2的中点P3,取P2P3的中点P4,……．

(1)比较线段OPn与OPn－1的大小:_________(n为大于1的整数);

(2)若OP＝1m,则从n＝________开始,线段Pn－1Pn＜1mm．

(《时代学习报》数学文化节试题)

8．以∠AOB的顶点O为端点引射线OC,使∠AOC∶∠BOC＝5∶4,若∠AOB＝15°,则∠AOC的度数是________．

(北京市“迎春杯”竞赛题)

9．公园里准备修5条直的甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设(　)．

A．9个　B．10个　C．11个　D．12个

(“希望杯”邀请赛试题)

10．如图,点A,B,C顺次在直线上,M是线段AC的中点,N是线段BC的中点,若想求出MN的长度,则只需条件(　)．

A．AB＝12　B．BC＝4　C．AM＝5　D．CN＝2

(海南省竞赛题)

(第10题)

(第11题)

11．如图,点B在线段AC上,且BC＝2AB,D,E分别是AB,BC的中点,则下列结论:①AB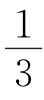＝AC;②B是AE的中点;③EC＝2BD;④DE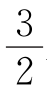＝AB．其中正确结论的个数有(　)．

A．1个　B．2个　C．3个　D．4个

对于问题4,读者可能会发现结果与已知数据的联系,是巧合还是必然?若是巧合,怎样解释;若是必然,如何证明．

12．如图,点O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE＝60°,∠BOE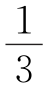＝∠EOC,则下列四个结论:①∠BOD＝30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对．则正确的个数有(　)．

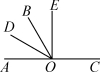
(第12题)

A．1个　B．2个　C．3个　D．4个

13．某手表每小时比准确时间慢3分钟,若在清晨4点30分与准确时间对准,则在当天上午手表指示时间为10点50分,则准确时间应是(　)．

A．11时　B．11时10分　C．11时20分

D．11时30分　E．11时40分

(国际中小学数学能力检测试题)

14．在图示的方格纸中,点A,B,C都在方格纸的交点上,则∠ACB＝(　)．

A．120°　B．135°

C．150°　D．165°

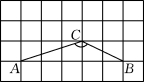
(第14题)

15．如图,某公司员工住在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一直线上,如图所示．公司的接送车打算在此间只设一个停靠点,为了使所有员工步行到停靠点的路程总和最小,那么停靠点的位置应在(　)．

A．A区　B．B区　C．C区　D．A,B两区之间

(江苏省竞赛题)

(第15题)

(第16题)

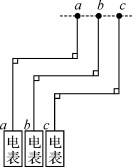
16．如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线(　)．

A．a户最长　B．b户最长

C．c户最长　D．三户一样长

(江西省南昌市中考题)

17．已知在直线上有n(n≥2的正整数)个点,每相邻两点之间的距离为1,从左边第1个点起跳,且同时满足以下三个条件:①每次跳跃均尽可能最大;②跳n次后必须回到第1个点;③这n次跳跃将每个点全部到达．设跳过的所有路程之和为Sn,求S25的值．

(四川省资阳市中考题)

18．小明在平面上标出了2007个点并画了一条直线l,他发现:这2007个点中的每一个点关于直线l的对称点仍在这2007个点中．请你说明:这2007个点中至少有1个点在直线l上．

(“希望杯”邀请赛试题)

19．已知∠AOB＝100°,∠COD＝40°,OE平分∠AOC,OF平分∠BOD(本题中的角均为大于0°且小于等于180°的角)．

(1)如图①,当OB,OC重合时,求∠EOF的度数;

(2)当∠COD从图①所示位置绕点O顺时针旋转n°(0＜n＜90)时,∠AOE－∠BOF的值是否为定值?若是定值,求出∠AOE－∠BOF的值,若不是,请说明理由;

(3)当∠COD从图①所示位置绕点O顺时针旋转n°(0＜n＜180)时,满足∠AOD＋∠EOF＝6∠COD,则n＝________．

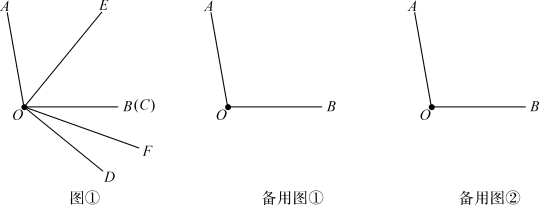
(第19题)

20．如图,A是数轴上表示数11的点,B是数轴上表示数28的点,C为数轴上一点,点C从点A出发,以每秒3个单位长度在数轴上匀速运动．

(第20题)

(1)当点C从点A出发,以每秒3个单位长度沿数轴正方向匀速运动,①点C运动3秒时,B,C两点间的距离为________(单位长度);

②若点M为线段OC的中点,点N为线段AC的中点,当点C运动多少秒时,点N为线段MC的三等分点;

(2)当点C以每秒3个单位长度沿数轴正方向匀速运动到B点时,改变方向后始终沿数轴负方向匀速运动,速度保持不变．点C从A点出发的同时,另一点D从原点出发,始终沿数轴正方向以每秒6个单位长度的速度匀速运动．数轴上两点之间的距离小于或等于10个单位长度时,称这两点处于“可视距离”,求点C和点D在整个运动过程中,有多少秒处于“可视距离”?

21．直线上分布着1990个点,我们来标出以这些点为顶点的一切可能线段的中点,试求至少可以得出多少个互不重合的中点．

(上海市竞赛题)

22．一直线从左到右顺次排列着1987个点:P1,P2,P3,…,P1987,已知Pk点是线段Pk－1Pk＋1的k等分点当中最靠近Pk＋1的那个分点(2≤k≤1986)．例如,P5点就是线段P4P6的5等分点中最靠近P6的那个点．如果线段P1P2的长度是1,线段P1986P1987的长度是l,求证:

(北京市竞赛题)

23．(1)现有一个19°的“模板”(如图),请你设计一种办法,只用这个“模板”和铅笔在纸上画出1°的角来;

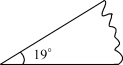
(第23题)

(2)现有一个17°的“模板”与铅笔,你能否在纸上画出一个1°的角来?

(3)用一个21°的“模板”与铅笔,你能否在纸上画出一个1°的角来?

对于(2)、(3)两问,如果能,请你简述画法步骤;如果不能,请你说明理由．

(“希望杯”邀请赛试题)

24．在图8×8方格表中,绘出一条闭合折线,使得:

(1)此折线仅与小方格的边平行或垂直,且不与自身相交;

(2)此折线经过每个小方格至多一次,且必须经过所有标记有小圈的小方格,但不一定要经过没标记的小方格;

(3)此折线在每一个有黑圈的小方格处必须转一个直角弯,但在黑圈之前与之后的一个小方格处不可以转弯;

(4)此折线在经过有白圈的小方格之前或之后(或两者)的一个小方格处,都必须转一个直角弯,但在有白圈的小方格处都不可以转弯．

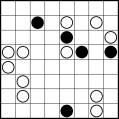
(第24题)

(青少年数学国际城市邀请赛试题)

25．平面上有七个点,它们之间可以连一些线段,使七点中的任意三点必存在两点有线段相连．问:至少要连多少条线段?证明你的结论．

(上海市竞赛题)

估算、证明、构造是解如第25题图形最值问题的基本方法,即先依据条件猜测最值,再证明没有超过它的值,最后构造一个图形说明此最值是可以达到的．

例1　(1)1　15　交点最多为

(2)10,450°　一共有10个角,分别为:∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE．其中∠AOE＝90°,∠BOD＝45°,∠AOB＋∠BOE＝90°,∠AOC＋∠COE＝90°,∠AOD＋∠DOE＝90°,∠BOC＋∠COD＝45°．故这10个角的度数和为90°×4＋45°×2＝450°．

例2　(1)B　MN＝AN－AM,PQ＝PA－QA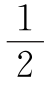＝(AN－AM)．

(2)D　由于沿AB对折时,上、下图形能够重合,恰好∠1＋∠9＝∠2＋∠6＝∠4＋∠8＝90°．

例3　600千米　设小镇为D,傍晚汽车在E休息,如图,则AD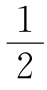＝DC,EB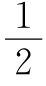＝CE,AD＋EB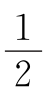＝DE＝200千米．

(例3)

例4　(1)当点A运动在点C左侧时,由6＋6t＝30＋18＋3t得t＝14;

当点A运动在点C右侧时,由6t－6＝30＋18＋3t得t＝18．

(2)A,B,C三点在数轴上表示的数分别为6t－30,10＋3t,18＋3t．

当点P运动在点N右侧时,PM＝－2,这种情形不存在．

例5　(1)∠COD＝40°

(2)∵∠DOE＝3∠AOE,∠COF＝3∠BOF,

∴设∠AOE＝x°,∠BOF＝y°,则∠EOD＝3x°,∠COF＝3y°,

∴∠CDO＝∠AOD＋∠BOC－∠AOB＝4x°＋4y°－120°

∠EOF＝∠EOD＋∠FOC－∠COD

＝3x°＋3y°－(4x°＋4y°－120°)＝120°－(x°＋y°),

∵∠EOF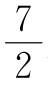＝∠COD,

∴120－(x＋y)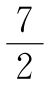＝(4x＋4y－120),∴x＋y＝36

∴∠EOF＝120°－(x＋y)°＝84°

(3)7．5或15或45

设旋转n°,对于∠IOM:当0＜n＜180时,∠IOM＝,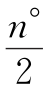

当180＜n＜300时,∠IOM＝180°－．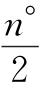

对于∠POI:当0＜n＜60时,∠POI＝30°－,

当60＜n＜180时,∠POI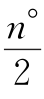＝－30°,

当180＜n＜240时,∠POI＝120°－,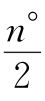

当240＜n＜300时,∠POI＝－120°．

(n＝60,240时,OP和OI重合)

分四种情况:

①如图①,0＜n＜60时,由,得n＝45,∴t＝7．5;

②如图②,60＜n＜180时,由,得n＝90,∴t＝15;

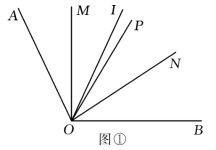
(例5)

③如图③,180＜n＜240时,由,得n＝180,∴t＝30(舍);

④如图④,240＜n＜300时,由,得n＝270,∴t＝45．

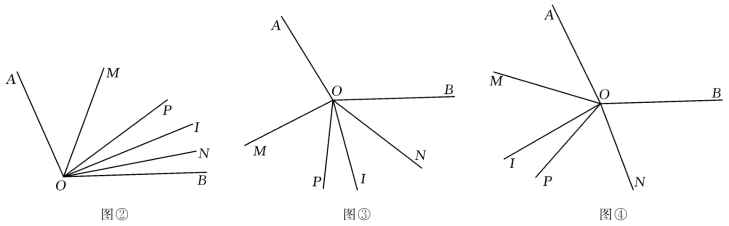
(例5)

例8　设从0时开始,过x分钟后分针与时针成60°的角,此时分针比时针多走了n圈(n＝0,1,2,3,…,11),则x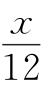－＝60n＋10,或x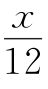－＝60n＋50,

解得x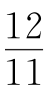＝(60n＋10)或x＝(60n＋50)．

分别令n＝0,1,2,3,…,11,即得本题的所有22个解(精确到秒):

0:54:33,2:00:00,3:05:27,4:10:55,5:16:22,6:21:49,7:27:16,8:32:44,9:38:11,10:43:38,11:49:05,1:16:22,2:21:49,3:27:16,4:32:44,5:38:11,6:43:38,7:49:05,8:54:33,10:00:00,11:05:27,0:10:55．

在12小时内,秒针相对于时针走了60×12－1＝719圈,所以秒针与时针共有719×2＝1438次成60°的角．

1．7

2．因每次操作后剩下的都是之前的,故六次操作后剩下

3．7　平面上n个不同的点最多可确定条直线．

4．128　假定有这样一条长方形的小路,宽1m,长16m,如图①．沿着这条小路的中间行走,显然行走路线的长为16m,这就说明行走路线的长与宽为1m的长方形小路的长是相等的．由于长方形场地充满了1m宽的小路,这便启发我们将长方形场地分割成8条宽1m、长16m的小路,如图②,于是这条小路的总长为16×8＝128(m)．

(第4题)

更一般情况是:若长方形的场地的长为a米,宽为b米,其中充满宽为c米的小路,则走完这条小路共走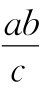 米．

5．40

6．15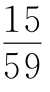设经过x秒时,OA与OB第一次垂直,又因为秒针1秒旋转6°,分针1秒旋转0．1°,于是有(6－0．1)t＝90,解得t＝15．

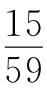7．(1)OPn＞OPn－1　当n为奇数时,OPn＜OPn－1;当n为偶数时,OPn＞OPn－1．

(2)10　∵Pn－1Pn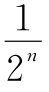＝ ,且,∴从n＝10开始,Pn－1Pn＜1mm．

8．8°20′或75°　9．B　10．A　MN＝AB．

11．C　12．D

13．B　设所求的准确时间为x小时,则

14．B

15．A　停靠点设在A,B,C三区,计算总路程分别为4500米,5000米,12000米,可排除选项B、C;设停靠点在A,B两区之间且距A区x米,则总路程为30x＋15(100－x)＋10(300－x)＝4500＋5x＞4500,又排除选项D．

16．D

17．当n为偶数时,Sn＝(1＋2＋3＋…＋n－1)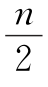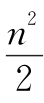＋＝;当n为奇数时,Sn＝(1＋2＋3＋…＋n－1)＋,故

18．假设这2007个点都不在直线l上,由于其中每个点Ai(i＝1,2,…,2007)关于直线l的对称点A′i仍在这2007个点中,所以A′i也都不在直线l上．也就是说,不在直线l上的点Ai(i＝1,2,…,2007)与Ai关于直线l对称的点A′i成对出现,即平面上标出的点的总数应是偶数个,与点的总数2007个相矛盾．因此,“这2007个点都不在直线l上”的假设不成立,即这2007个点中至少有1个点在直线l上．

19．(1)∠EOF＝70°

(2)当0＜n≤80时,∠AOE－∠BOF＝30°为定值;当80＜n＜90时,∠AOE－∠BOF＝110°－n°不为定值．

(3)30或50或90

20．(1)①8

21．我们将已知的1990个点中距离最远的两点记为A,B,A点与除B点以外的1988个点构成1988条线段,这些线段的中点都不重合,且到A点的距离小于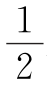AB;对于B点作同样的考虑,又可得到1988个互不重合的中点,且到B点的距离小于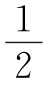AB．再加上AB的中点,共得互不重合的中点1988×2＋1＝3977个．这说明中点的个数不会小于3977．另一方面,当这1990个点每相邻两点都相等时,不同的中点的个数正好是3977．所以所有可能线段的不同中点数的最小数目是3977．

23．若只连续使用模板,则得到的是一个19°(或17°或21°)的整数倍的角,其实,解题的关键是在于能否找到19°(或17°或21°)的一个倍数与某个特殊角的某个倍数相差1°,设“模板”角度为α,假设可由k个α角与t个180°角画出1°的角来,即k,t满足kα－180t＝1．

(1)当α＝19°时,取k＝19,t＝2,即用模板连续画出19个19°的角,得到361°的角,去掉360°的周角,即得1°的角．

(2)当α＝17°时,即17k－180t＝1,得k＝53,t＝5是一组解,即用模板连续画53个17°的角,得到901°的角,除去两个周角和一个平角,即得1°的角．

(3)当α＝21°时,即21k－180t＝1无整数解,不能用21°的模板与铅笔画出1°的角．

24．根据题目的规定先确定每个带圈的方格所必须连接的折线,可得图甲;

在图甲的基础上,再连接必须连接的线路,可得图乙;

最后,根据图乙所得的结果,继续加入必须连接的线段而完成整条折线,如图丙．

(第24题)

25．(1)若某点A不作为线段的端点,则其他六点每两点都有线段相连,共要连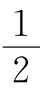×6×5＝15条线段．

(2)若点A只作为一条线段的端点,则不与A相连的五点之间每两点都有线段相连,至少要连×5×4＝10条线段,共要连11条线段．

(3)若点A只作为两条线段AB,AC的端点,则不与A相连的四点之间每两点都有线段相连,至少要连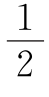×4×3＝6条线段．从点B至少还要引出一条线段,此时,至少有2＋6＋1＝9条线段．

(4)若每一点至少作为三条线段的端点,则至少要连条线段．注意到线段的条数为整数,故此时至少要连11条．

如图表明九条线段已经足够了．

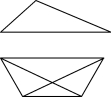
(第25题)