【摘要】:璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西.”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意.知能概述图形有具体的,有抽象的;有平面的,有立体的.它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录.立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方
璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西.”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意.
知能概述
图形有具体的,有抽象的;有平面的,有立体的.它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录.
立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方向看立体图形,用平面去截立体图形.
观察归纳、操作实验、展开想象、推理探索是解立体图形问题的基本方法.
折叠——平面图形立体化,展开——立体图形平面化,折与展,将我们的思维带入到更深刻的境地.
我们既要能将一个立体图形展开得到它的各个面,又要能将一个平面图形折叠起来,想象出它的立体形状.
问题解决
例1 (1)如图是一个正方体的平面展开图,若该正方体相对的两个面上的代数式的值相等,则z+y-x的值是_________.
(“希望杯”邀请赛试题)
(2)设5cm×4cm×3cm长方体的一个表面展开图的周长为ncm,则n的最小值是_________.
(江苏省竞赛题)
柏拉图说:“上帝在不断地制作几何图形.”
——普卢塔克
从多面体到足球,从蜂房结构、气泡的三重联结到多面体的面,2025年美丽雄伟的水立方就矗立在我们面前.
数学家从大自然中获得灵感,而数学帮助他们找到隐藏在深处的数学规律和美.
解题思路 对于(1),由折叠还原成正方体,建立方程组;对于(2),把展开图的周长用相应代数式表示.
例2 如图是一个立体图的主视图、左视图和俯视图(图中单位为厘米),则立体图形的体积为( )立方厘米.
A.π B.2π C.3π D.4π
(“华罗庚金杯”少年数学邀请赛试题)
解题思路 先确定该立体图的大致形状.
例3 如图是由若干个正方体形状木块堆成的,平放于桌面上,其中,上面正方体的下底面四个顶点恰是下面相邻正方体的上底面各边的中点,如果最下面的正方体的棱长为1,且这些正方体露在外面的面积和超过8,那么正方体的个数至少是多少?按此规律堆下去,这些正方体露在外面的面积和的最大值是多少?
(《时代学习报》数学文化节试题)
解题思路 所有正方体侧面面积和再加上所有正方体上面露出的面积和,就是需要求的面积.从简单入手,归纳规律.
从不同的方向看,既要能从三视图中想象出立体图形,又要能从给定的立体图形想象出从不同方向看它时的不同形状.
例4 由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,求n的值.
(“希望杯”邀请赛试题)
解题思路 本例可以在“脑子”中想象完成,也可以用实物摆一摆.从操作实验入手,从俯视图可推断左视图只能有两列,由主视图分析出俯视图每一列小正方形的块数情况是解本例的关键,而有序思考、分类讨论,则可避免重复与遗漏.
例5 (1)1000个单位正方体合在一起成为一个棱长是10个单位的大正方体,油漆后再分开为原来的正方体.求这些单位正方体中至少有一面被油漆的个数.
(2)一木制正方体的边长为n单位(这里n>2的整数).将此正方体的表面全部涂上黑色的漆,再用平行于此正方体各个面的平面将正方体切割成n3个边长为1单位的小正方体.若恰有一面涂有黑漆的小正方体的个数正好等于六面全无涂漆的小正方体的个数,求n的值.
(美国高中数学考试题)
解题思路 对于(1),先确定单位正方体所有面未油漆过的个数;对于(2),建立n的方程.
例6 要把一个正方体分割成49个小正方体(小正方体大小可以不等),画图表示.
(国际数学竞赛题)
分析与解 本例是一道图形分割问题,解答本例需要较强的空间想象能力和推理论证能力,需要把图形性质与计算恰当结合.
为方便起见,设正方体的棱长为6个单位,首先不能切出棱长为5的立方体,否则不可能分割成49个小正方体.
给出两种视图,要求画出第3个视图或确定立方块的块数,这样的问题答案常常不唯一.解题的关键是:俯视图就是立体图形最底层对应的平面图形,主视图中每列小正方形的个数就是俯视图中每列数中最大的数值.
对于例6,有下列一般的结论:
一个立方体可以分割成n个小立方体,这里n=1,8,15,20,22,27,29,34,36,38,39,41,43,45,46及大于47的整数.
设切出棱长为1的正方体有a个,棱长为2的正方体有b个,如果能切出1个棱长为4的正方体,
则有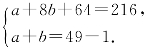 解之得b=14
解之得b=14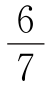 ,不合题意,所以切不出棱长为4的正方体.
,不合题意,所以切不出棱长为4的正方体.
设切出棱长为1的正方体有a个,棱长为2的正方体有b个,棱长为3的正方体有c个,
则 解得a=36,b=9,c=4,
解得a=36,b=9,c=4,
故可分割棱长分别为1,2,3的正方体各有36个、9个、4个,分法如图所示.
例7 雨哗哗地不停地下着,如果在雨地里放一个如图①(单位:厘米)那样的长方体的容器,雨水将它注满要用1小时(不考虑溅出).
有下列A—E不同的容器(图②),雨水注满这些容器各需多长时间?
(日本算数奥林匹克竞赛题)
分析与解 题中“雨哗哗地不停地下着”这一条件,也可以理解为雨均匀地下(这与日常生活中的降雨略有不同,生活中降雨可能会时大时小,并不均匀).雨水从敞口部分垂直落入到容器内,我们就可以把“敞开面”(即图中所示的阴影面)叫作“接雨面”.
一个立方体能否分割成47个小立方体,至今还是一个未被解决的问题.
20世纪初,伟大的法国建筑家列·柯尔伯尔曾说:“到目前为止,我们从没有生活在这样的几何时期,周围的一切都是几何学.”
作为空间形式的科学的几何学,视觉思维占主导,在培养直觉思维、洞察力、逻辑推理能力等方面具有无可替代的作用.
图①所示的长方体容器,“接雨面”与底面大小相同,雨水将它注满需要1小时,也就是说1小时后该容器内雨水的深度是10厘米.如果容器的高度不止10厘米,而是无限的,那么2小时后容器内雨水的深度将会是20厘米,以后每过1小时雨水的深度就会增加10厘米;如果在长方体容器中垂直放入一个很薄的挡板(其厚度忽略不计),将大容器分成两个小容器(如图③所示).小容器的“接雨面”变小了,但每个小容器的“接雨面”与底面大小仍然相同,那么1小时后,每个小容器内雨水的深度还是10厘米(因为忽略了挡板的厚度,它不占原来长方体容器的容积).通过上述分析与假设,我们可得出如下结论:只要容器的“接雨面”与底面大小相同,1小时后容器内雨水的深度就是10厘米.
根据结论,观察图②所示的五种容器,其中A,B,E三种容器的“接雨面”与底面大小相同.
A容器高10厘米,雨水注满该容器需要1小时;B容器高30厘米,雨水注满该容器需要3小时;E容器高20厘米,雨水注满该容器需要2小时.
剩下C,D两种容器,它们的“接雨面”与底面大小不同,可先将其转化为“接雨面”与底面大小相同的容器(如图④所示).此时,C容器的高变为30厘米,雨水注满需3小时;D容器的高度为15厘米,雨水注满需1.5小时.
欧拉公式
瑞士数学家欧拉是历史上最多产的数学家,一生发表过800多篇(本)论文、著作.他28岁时解决了著名的哥尼斯堡七桥问题,其主要思想是将原问题转化为一笔画问题.
法国著名数学家拉普拉斯曾说:“读读欧拉,他是我们所有人的导师.”
例8 建立模型
18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.
(1)根据上面多面体模型,完成表格中的空格:
超人的毅力、非凡的才能、过人的数学直觉,成就了历史上最多产的伟大数学家欧拉.通过这本书,我们可以从欧拉的数学直觉,以及直觉在科学发展中所起的作用得到宝贵的启示.
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是________.
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是________.
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
模型应用
如图,有一种足球是由数块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等,求正五边形、正六边形个数.
(浙江省宁波市中考题改编)
解题思路 对于模型应用,有不同的解法,请读者一试.
1.如图是一个3×3×3的正方体,现从其表面任意拿出一个1×1×1的小正方体,则剩余立体图形的表面积为_________(写出所有可能的结果).
(“理想杯”邀请赛试题)
(第1题)
(第2题)
(第3题)
2.用七块棱长为1cm的小正方块堆成一立体,其俯视图如图所示,则共有________种不同的堆法(经旋转能重合的算一种堆法).
(“华罗庚金杯”少年数学邀请赛试题)
3.如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要________个小正方体,王亮所搭几何体的表面积为________.
(山东省青岛市中考题)
4.王老师将底面半径为20厘米、高为35厘米的圆柱形容器中的果汁全部倒入如图所示的杯子中,若杯口直径为20厘米,杯底直径为10厘米,杯高为12厘米,杯身长13厘米,则果汁可以倒满_________杯.
(第4题)
(世界数学团体锦标赛试题)
5.将一个正方体的表面都染成红色,再切割成n3(n>2)个相同的小正方体,若只有一面是红色的小正方体数目与任何面都不是红色的小正方体的数目相同,则n=_________.
(全国初中数学联赛题)
6.将27个大小相同的小正方体组成一个大正方体,现将大正方体各面上的某些小方格涂上黑色,如图所示,而且上与下、前与后、左与右相对的两个面上的涂色方式相同,这时,至少有一个面上涂有黑色的小正方体的个数是( ).
A.18 B.20 C.22 D.24
(“希望杯”邀请赛试题)
(第6题)
(第7题)
7.如图①,将正方体的左上部位切去一个小三棱柱(图中M,N都是正方体的棱的中点),得到如图②所示的几何体,设光线从正前方、正上方、正左方照射图②中的几何体,被光照射到的表面部分面积之和分别为S前,S上,S左,那么( ).(https://www.chuimin.cn)
A.S前=S上=S左 B.S前<S上=S左
C.S上<S左<S前 D.S上<S左=S前
8.设有一立体的三视图如图所示:
(第8题)
则该立体体积为( ).
(浙江省竞赛题)
9.由若干个单位立方体组成一个较大的立方体,然后把这个大立方体的某些面涂上油漆,油漆干后,把大立方体拆开成单位立方体,发现有45个单位立方体上任何一面都没有漆,那么大立方体被涂过油漆的面数是( ).
A.1 B.2 C.3 D.4
(“创新杯”邀请赛试题)
10.小明把棱长为4的正方体分割成了29个棱长为整数的小正方体,则其中棱长为1的小正方体的个数是( ).
A.22 B.23 C.24 D.25
(浙江省竞赛题)
11.如图,从长、宽、高分别为15cm,5cm,4cm的长方体中切割走一块长、宽、高分别为ycm,5cm,xcm的长方体(x,y为整数),余下的部分的体积为120cm3,求x,y的值.
(第11题)
(“华罗庚金杯”少年数学邀请赛试题)
12.把两个长为3cm、宽2cm、高1cm的小长方体先粘合成一个大长方体,再把它切分成两个大小相同的小长方体,那么一个小长方体的表面积最多可比起初一个小长方体的表面积大多少?
(江苏省竞赛题)
13.如图①,这是由6个单位正立方体所摆放出的“立体示意图”,我们在每个最上方的面涂上斜线.图②是图①的“轮廓图”.若已知图③是由18个单位正立方体所摆放出的立体图的“轮廓图”,请画出它的“立体示意图”,并且在每个最上方的面涂上斜线.
(国际少年数学精英大会自主试题)
(第13题)
14.如图,上面是一个底面直径和高都为10厘米的圆柱,下面是一个棱长为10厘米的正方体,从上到下挖去一个直径为6厘米的圆柱后,问所得几何体的表面积是多少平方厘米(π取3)?
(世界数学团体锦标赛试题)
(第14题)
(第15题)
15.如图,ABCD是长方形,BC=6cm,AB=10cm,AC和BD是对角线,图中的阴影部分以CD为轴旋转一周,求阴影部分扫过的立体图形的体积(π取3.14).
(“华罗庚金杯”少年数学邀请赛试题)
16.我们在一个立方体的每个面上写一个正整数,然后,在每个顶点处再写一个数,该数等于过这个顶点的三个面上的整数的乘积.已知该立方体各个顶点上的数字之和为70,求该立方体各个面上的数字之和.
(斯洛文尼亚数学奥林匹克试题)
例1 (1) -3 由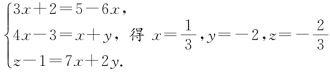 ,原式=-3.
,原式=-3.
(2)50 长方体的展开图的周长为8c+4b+2a,
周长的最小值为8×3+4×4+2×5=50.
(例1)
例2 B
例3 4 9 最下面正方体1个面的面积是1,侧面露出的面积和是4,每相邻两个正方体中上面的1个正方体每个面的面积都正好是其下面正方体1个面面积的 ,所有正方体侧面面积之和加上所有正方体的上面露出的面积和(正好是最下面正方体上底面的面积1)即是这些正方体露在外面的面积和.如:
,所有正方体侧面面积之和加上所有正方体的上面露出的面积和(正好是最下面正方体上底面的面积1)即是这些正方体露在外面的面积和.如:
……
故随着小正方体木块的增加,其外露的面积之和都不会超过9.
例4 (1)左视图有以下5种情形:
(例4)
(2)n=8,9,10,11.
例5 (1)大正方体内有83=512个正方体是所有面未油漆过的,故有103-83=488个正方体至少有一面油漆过.
(2)有一面涂漆的小正方块有6(n-2)2个,六个面均未涂漆的小正方块有(n-2)3个,由6(n-2)2=(n-2)3,得n=8.
例8 (1)6 6 V+F-E=2 (2)20
(3)这个多面体的面数为x+y,棱数为 =36(条).
=36(条).
根据V+F-E=2,可得24+(x+y)-36=2,∴x+y=14.
模型应用
设足球表面的正五边形有x个,正六边形有y个,总面数F为x+y个.因为一条棱连着两个面,所以足球表面的棱数E为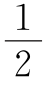 (5x+6y),又因为一个顶点上有三条棱,一条棱上有两个顶点,所以顶点数V=
(5x+6y),又因为一个顶点上有三条棱,一条棱上有两个顶点,所以顶点数V=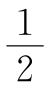 (5x+6y)·
(5x+6y)·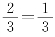 (5x+6y).
(5x+6y).
由欧拉公式V+F-E=2得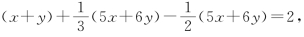
解得x=12.
所以正五边形有12个.
又根据每个正五边形周围连着5个正六边形,每个正六边形又连着3个正五边形,所以六边形个数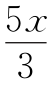 =20,即有20个正六边形.
=20,即有20个正六边形.
1.54,56,58 原正方体的表面积为9×6=54,当拿出的小正方体位于角上时,表面积不变;当拿出的小正方体位于边上时,表面积增加2平方单位;当拿出的小正方体位于中间时,表面积增加4个平方单位.
2.5 因底层已用了四块小正方体,第五块、第六块、第七块只有如图五种放置方法:
(第2题)
3.19 48 在张明摆放的基础上,若用最少的小正方体拼成一个大长方体,则需要9×4=36块小正方体,而张明已用17块,所以王亮至少需要36-17=19块;张亮摆的几何体如图所示,从前、后看,其表面积为9,从左、右看,其表面积为7,从上、下看,其表面积为8,所以整个几何体的表面积为2×(9+7+8)=48.
4.20 如图,由题意知AB=10cm,CD=5cm,AC=12cm,BD=13cm,过点D作DE垂直AB于点E,则DE=12cm,于是Rt△BDE中BE=5cm.
延长AC,BD交于F,则由CD∶AB=5∶10=1∶2知CF=12cm,AF=24cm.
于是一个杯子的容积等于两个圆锥的体积之差,即
(第3题)
而大容器内果汁的体积是π×202×35=14000π(cm3),
所以果汁可以倒满14000π÷700π=20(杯).
5.8 只有一个面染红色的小正方体的总数为6(n-2)2个,任何面均不是红色的小正方体的总数为(n-2)3个,由题意知6(n-2)2=(n-2)3,解得n=8.
6.B 共有7个小正方体没有被涂黑.
7.C
8.A 该几何体是一个圆柱与一个长方体的合成,其中重叠部分体积为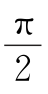 ,故该几何体的体积为
,故该几何体的体积为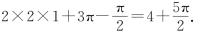
(第4题)
9.D 设大立方体的棱长为n,n>3,若n=6,即使6个面都油漆过,未油漆的单位立方体也有43=64个,大于45,故n=4或5.除掉已漆的单位立方体后,剩下未漆的构成一个长方体,设其长、宽、高分别为a,b,c,abc=45,只能是3×3×5=45,故n=5.
10.C 若分割出棱长为3的正方体,则棱长为3的正方体只能有1个,余下的均是棱长为1的正方体,共37个不满足要求.设棱长为2的正方体有x个,棱长为1的正方体有y个,则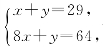 得
得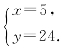
11.如图,将“L”形物体补上长方体M后,M的体积为15×5×4-120=180,侧面N的面积为180÷5=36,而36=1×36=2×18=3×12=4×9=6×6,只有x,y分别为3,12符合题意.
12.设原先的小长方体为A型体,将这两个A型体最小面1厘米×2厘米粘合成一个大长方体:1厘米×2厘米×6厘米.将这大长方体从最小边开始,在面1厘米×6厘米中间切开,成为两个B型小正方体:0.5厘米×2厘米×6厘米.一个A型小长方体表面积S1=2(1×2+1×3+2×3)=22(厘米2),一个B型小长方体表面积S2=2(0.5×2+0.5×6+2×6)=32(厘米2).一个B型小长方体表面积与一个A型小长方体表面积可以相差10厘米2,这是差的最大值.
13.答案不唯一,下列示意图供参考.
(第11题)
(第13题)
14.正方体四周的面积和为10×10×4=400(平方厘米),
正方体的下底面去掉一个小圆后,面积为10×10-32π=100-9π(平方厘米),
正方体的上底面去掉一个圆后,面积为10×10-52π=100-25π(平方厘米),
正方体上面的圆柱的侧面积为10π×10=100π(平方厘米),
圆柱上底面去掉一个小圆后,面积是π(52-32)=16π(平方厘米).
内部空心圆柱的侧面积为6π×20=120π(平方厘米),
故所求表面积为:
400+(100-9π)+(100-25π)+100π+16π+120π=600+202π(平方厘米).
当π=3时,上式=1206(平方厘米).
15.设三角形BCO以CD为轴旋转一周所得到的立体(如图)的体积是V,V等于高为10cm、底面半径为6cm的圆锥的体积减去2个高为5cm、底面半径是3cm的圆锥的体积,即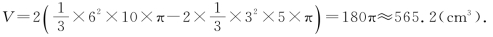
(第15题)
16.设立方体的每个面上的数字分别为a1,a2,a3,a4,a5,a6,在顶点上所写的数分别为a1a2a5,a2a3a5,a3a4a5,a4a1a5,a1a2a6,a2a3a6,a3a4a6,a4a1a6.于是,可得
70=a1a2a5+a2a3a5+a3a4a5+a4a1a5+a1a2a6+a2a3a6+a3a4a6+a4a1a6
=(a5+a6)(a1a2+a2a3+a3a4+a4a1)
=(a1+a3)(a2+a4)(a5+a6).
由于70=2×5×7,显然,在乘积(a1+a3)(a2+a4)(a5+a6)中,一个因子等于2,一个因子等于5,另一个因子等于7.
于是,所求的和为a1+a2+a3+a4+a5+a6=2+5+7=14.

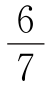 ,不合题意,所以切不出棱长为4的正方体.
,不合题意,所以切不出棱长为4的正方体. 解得a=36,b=9,c=4,
解得a=36,b=9,c=4,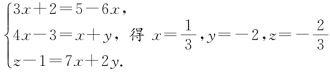 ,原式=-3.
,原式=-3. ,所有正方体侧面面积之和加上所有正方体的上面露出的面积和(正好是最下面正方体上底面的面积1)即是这些正方体露在外面的面积和.如:
,所有正方体侧面面积之和加上所有正方体的上面露出的面积和(正好是最下面正方体上底面的面积1)即是这些正方体露在外面的面积和.如: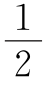 (5x+6y),又因为一个顶点上有三条棱,一条棱上有两个顶点,所以顶点数V=
(5x+6y),又因为一个顶点上有三条棱,一条棱上有两个顶点,所以顶点数V=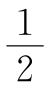 (5x+6y)·
(5x+6y)·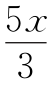 =20,即有20个正六边形.
=20,即有20个正六边形.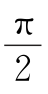 ,故该几何体的体积为
,故该几何体的体积为





相关推荐