精英数学大视野·七年级2020：第18讲平面直角坐标系

笛卡儿(1596—1650),17世纪法国著名哲学家、数学家,1637年出版了著名的哲学著作《方法论》一书,在这本书中,他引进变量概念,使运算关系符号化,创建坐标系,建立解析几何学,从初等数学发展到近代数学,解析几何的诞生是一个伟大的里程碑．

知能概述

在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,从而坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,是用代数方法研究几何图形的有力工具．

平面直角坐标系问题,涉及点的坐标意义、坐标轴上点的坐标特征、对称点的坐标特点、象限内点的坐标符号特点,善于促成坐标与线段的转化是解相关问题的关键．

问题解决

例1　(1)若P(a,8)和Q(7,b)关于y轴对称,则(a＋b)2010＝________．

(湖北省黄冈市竞赛题)

(2)如图,是5×5的网格．一只蚂蚁在网格左下角(0,0)位置,每次能向上走一格或者向右走一格,要到达右上角(5,5)的位置,且不能经过点(1,1),(1,4),(4,1)和(4,4),则不同的走法共有________种．

(青少年数学国际城市邀请赛)

解题思路　对于(2),以(0,0)为起点,渐次地寻找到达每一个点的不同走法的种数,并在相应的位置上记录下来,并由此写出走法的规律．

当学生在解那些对他来说并不太容易的题目时,他学会了面对挫折且锲而不舍,学会了当灵感到来后的全力以赴．如果在学校里有机会尝尽为求解而奋斗的喜怒哀乐,那么他的数学教育就在最重要的地方成功了．

——波利亚

笛卡儿说有三个梦引导了“一门奇特的科学”和“一项惊人的发现”,这就是科学史上有名的笛卡儿之梦．对笛卡儿而言,怀疑是一门艺术,是一种必要的手段,它使人们脱离感觉的影响而获得解放．

例2　设平面直角坐标系的轴以1厘米作为长度单位,△PQR的顶点坐标分别为P(0,3),Q(4,0),R(k,5),其中0＜k＜4．若该三角形的面积为8厘米2,则k的值是(　)．

(澳洲数学竞赛题)

解题思路　通过作辅助线,把△PQR的面积表示成其他图形面积的和差,建立k的方程．

(例2)

例3　(1)如图①,将边长为1的正方形OAPB沿x轴正方向连续翻转2006次,点P依次落在点P1,P2,P3,P4,…,P2006的位置,求点P2006的横坐标．

(广东省竞赛题)

(2)如图②,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3…均在格点上,其顺序按图中“➝”方向排列．如:P1(0,0),P2(0,1),P3(1,1),P4(1,－1),P5(－1,－1),P6(－1,2)…根据这个规律,求点P2016的坐标．

(岳阳市中考题)

在平面直角坐标系中,由坐标找点和由点求坐标是“数”与“形”相互转换的最基本形式．点的坐标是数与形结合的桥梁,求点的坐标的基本方法有:

(1)求相应线段长;

(2)解方程组．

现阶段求线段的长度,因受知识的制约,故常借助面积求解．

点的坐标变化规律有下面两种表现形式:

(1)循环规律;

(2)递进规律．

其中递进规律又体现为:按一定规律分类,或点的位置按一定程序变化．

(3)如图③,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去．

①在图中画出点M,N,并写出点M,N的坐标;

②求经过第2008次跳动之后,棋子落点与点P的距离．

(安徽省竞赛题)

解题思路　操作实验,观察发现,从寻找点的坐标变化规律入手．

例4　如图①,已知四边形OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE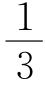＝AB,点F在OC上,且OF＝OC．点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值．

(“创新杯”竞赛题)

例5　下象棋是很多人喜爱的事,你知道象棋里充满着数学问题吗?如图①,象棋盘上有一只马,它跳七步能回到原来的位置上吗?若能,请给出一种跳法;若不能,请说明理由．

分析与解　不论怎么跳,马都不能回到原来的位置,理由如下:

恰当地建立坐标系,以数助形,这种解决问题的方法为坐标法．

例5更一般的结论是:只要马跳步的次数是奇数,就不能回到原来的位置．若马跳了n步后回到原来的位置,则跳的步数必为偶数．

如图②,我们可在棋盘上建立直角坐标系,并设这只马所在的位置P的坐标为(x0,y0)．那么,马跳一步后的位置的坐标应为(x0＋x1,y0＋y1),这里的x1和y1只可能是1,－1,2,－2这四个数中的一个(想一想,为什么)．

同样,跳第二步后,马所在的位置的坐标应为(x0＋x1＋x2,y0＋y1＋y2),这里的x2和y2也只可能是1,－1,2,－2．依此类推,跳七步后,马所在的位置的坐标为(x0＋x1＋x2＋x3＋x4＋x5＋x6＋x7,y0＋y1＋y2＋y3＋y4＋y5＋y6＋y7)．如果这时马又回到原来的位置(x0,y0),那么有x0＋x1＋x2＋x3＋x4＋x5＋x6＋x7＝x0,y0＋y1＋y2＋y3＋y4＋y5＋y6＋y7＝y0．

也即x1＋x2＋x3＋x4＋x5＋x6＋x7＝0,y1＋y2＋y3＋y4＋y5＋y6＋y7＝0．

将两式相加,有(x1＋y1)＋(x2＋y2)＋(x3＋y3)＋(x4＋y4)＋(x5＋y5)＋(x6＋y6)＋(x7＋y7)＝0．

由于上式中14个数都只能取1,－1,2,－2,而且每一次跳的两个坐标之和不能为0,4,－4,2和－2,因此x1＋y1,x2＋y2,x3＋y3,x4＋y4,x5＋y5,x6＋y6,x7＋y7这七个数只能取1,－1,3,－3．

但是不论怎样取法,由于奇数个奇数相加的和为奇数,所以这样取出的七个数的和不可能等于0．故马跳七步不可能回到原来的位置．

坐标化

恰当地建立坐标系,以数助形,这种解决问题的方法称为坐标化,坐标化的思想就是对应思想．坐标化使相关问题代数化,即找出相关问题涉及点的坐标或应满足的关系式、方程,通过讨论关系式、方程来研究问题．

例6　一片10英尺宽17英尺长的长方形地板用170块一英尺的正方形瓷砖铺好．一只虫子从一个角落沿着直线爬到对角,包括第一块和最后一块瓷砖,这只小虫爬过了多少块瓷砖?

(美国数学竞赛题)

解题思路　如图示,建立直角坐标系,设小虫的初始点为O(0,0),目标点为P(17,10),先求出小虫与17条纵线的交点分别为,…,A17(17,10);再求出小虫与10条横线的交点分别为,…,B10(17,10)．由于10与17是互素的,所以共有26个不同的交点,小虫每爬到一个交点处,意味着它爬过了一块瓷砖,即小虫共爬过了26块瓷砖．

思则有路

在数学问题的解决过程中,伴随着一系列的心智活动,无论进行过程是否顺利,都给人以启迪和力量．

“细雨湿衣看不见,闲花落地听无声．”

在挑战数学奥林匹克问题的征途中,我们的知识、方法、能力、智慧、意志力悄然得以增长．

数学知识具有严密的逻辑性和系统性,各分支之间存在着紧密的内在联系．“迁移”是融合各分支的关键．

“迁移”即运用一种思想方法对另一种数学知识或问题产生作用,是一种“融合性”的思维策略,其实质是以彼之法合此之理．

1．如图,在平面直角坐标系中,点B的坐标是(1,0),若点A的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是_________．

(河南省竞赛题)

(第1题)

(第2题)

(第3题)

2．如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),……根据这个规律,第2012个点的横坐标为________．

(山东省泰安市中考题)

3．如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标．如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(－1,2),那么,2004的对应点的坐标是________．

(江苏省南京市江宁区竞赛题)

4．在平面直角坐标系中,已知A(7,0),B(9,5),P为坐标轴上一点,且S△PAB＝50,那么,点P的坐标是_________．

(“创新杯”竞赛题)

5．如图,点O是坐标原点,折线ADC将△AOB的面积二等分,若点A(3,8),D(8,2),C(2,0),则点B的坐标为_________．

(第5题)

(世界数学团体锦标赛试题)

6．若a为整数,且点M(3a－9,2a－10)在第四象限,则a2＋1的值为(　)．

A．17　B．16　C．5　D．4

(黑龙江省哈尔滨市竞赛题)

7．如图,在平面直角坐标系中,已知A(－2,0),B(－1,2),C(1,0),连接AB,AB的中点为D,连接OB交CD于点E,则四边形DAOE的面积为(　)．

A．1　B．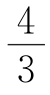

(第7题)

C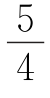．　D．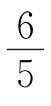

(山东省菏泽市中考题)

8．正方形ABCD在坐标系中的位置如图,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为(　)．

A．(－2,2)　B．(4,1)

C．(3,1)　D．(4,0)

(“希望杯”邀请赛试题)

(第8题)

(第9题)

9．如图,一个粒子在第一象限内及x,y轴上运动,在第一分钟内它从原点运动到(1,0),而后它接着按图所示在x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么,在1989分钟后这个粒子所处的位置是(　)．

A．(35,44)　B．(36,45)

C．(37,45)　D．(44,35)

(美国数学竞赛题)

10．一步之遥

姜文在其导演的电影《一步之遥》中饰演“马走日”,该名字取自中国象棋中“马”的走法．

中国象棋,“马”走“日”字,即马走一步可以从“日”字形长方格的一个顶点走到对角的另一个顶点,当n是自然数时,马从棋盘上的点A走到点B,所走的步数不可能是(　)．

(第10题)

A．2015n2＋2013n　B．2014n＋2015

C．2014n3＋2015　D．2013n＋2014

(《时代学习报》数学文化节试题)

11．已知在平面直角坐标系中,O为坐标原点,点A的坐标为(a,0),点B的坐标为(b,2),点C的坐标为(c,d),其中a,b,c满足方程组

(1)若点C到x轴的距离为6,则d的值为________;

(2)连接AB,线段AB沿y轴方向平移,线段AB扫过的面积为15,求点B的横坐标;

(3)连接AB,AC,BC,若△ABC的面积小于等于10,求d的取值范围．

12．阅读理解

我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、O(x2,y2)的对称中心的坐标为

观察应用

(1)如图,在平面直角坐标系中,若点P1(0,－1),P2(2,3)的对称中心是点A,则点A的坐标为________．

(2)另取两点B(－1．6,2．1),C(－1,0)．有一电子青蛙从点P1处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到P4关于点A的对称点P5处……则点P3,P8的坐标分别为________、_______．

(第12题)

拓展延伸

(3)求出点P2012的坐标．

(四川省内江市中考题)

13．约翰获得了亚当的藏宝图,亚当藏宝的点(x,y)为整点．他在藏宝图上标上了x2＋y,x＋y2的值,且它们不等．证明:约翰只能在一个地方挖掘才能找到宝藏．

(英国数学奥林匹克试题)

14．AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8)．若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积．

(1)求点P的坐标．

(2)试比较∠PAD和∠POC的大小,并说明理由．

(“创新杯”竞赛题)

15．一只青蛙在平面直角坐标系上从点(1,1)开始,可以按照如下两种方式跳跃:①能从任意一点(a,b),跳到点(2a,b)或(a,2b);②对于点(a,b),如果a＞b,则能从(a,b)跳到(a－b,b);如果a＜b,则能从(a,b)跳到(a,b－a)．例如,按照上述跳跃方式,这只青蛙能够到达点(3,1),跳跃的一种路径为:(1,1)→(2,1)→(4,1)→(3,1)．请你思考:这只青蛙按照规定的两种方式跳跃,能到达下列各点吗?如果能,请分别给出从点(1,1)出发到指定点的路径;如果不能,请说明理由．

(1)(3,5);(2)(12,60);(3)(200,5);(4)(200,6)．

(浙江省竞赛题)

16．设n和m为任意正整数,棋子马在坐标(n,m)处,每步横行n格然后直行m格,或直行n格然后横行m格．求证:在无限大的方格棋盘上,可用黑白两色染方格,使(n,m)处的马每步的起点与终点总是不同色．

(环球城市竞赛题)

17．在平面直角坐标系中,若某点的横、纵坐标均为有理数,则称该点为“有理点”;否则,称为“无理点”．在平面直角坐标系中任作一个正五边形,在其五个顶点中,有理点与无理点哪个多?证明你的结论．

(中国东南地区数学奥林匹克竞赛题)

例1　(1)1　a＝－7,b＝8,原式＝(－7＋8)2010＝1．

(2)34　如图所示．

例2　B　如图S①＋S②＋S③＋S△PQR＝4×5,

即,解得

例3　(1)正方形OAPB沿x轴正方向连续翻转4次,也就是正方形OAPB沿x轴滚动一周,点P的横坐标增加4(其中从点P→P1→P2→P3→P4,横坐标分别增加2,1,0,1)．因2006＝501×4＋2,正方形OAPB滚动501周后又翻转了2次,故点P2006的横坐标为－1＋501×4＋2＋1＝2006．

(2)点P2016位于第四象限,坐标为(504,－504)．

(3)①M(－2,0),N(4,4)．

②棋子落点坐标变化的规律是棋子每跳动3次后又回到点P处．因2008＝669×3＋1,故经过第2008次跳动后,棋子落在点M处,则,即棋子落点与P点的距离为22．

(例1)

(例2)

(例3)

1．(b＋1,－a＋1)

2．45　以最外边的正方形边上的点为准,点的总个数等于该正方形右下角(即x轴上)的点的横坐标的平方．

3．(1,－22)　所有奇数的平方数都在第四象限的角平分线上,且数(2n＋1)2对应点的坐标为(n,－n),于是数2025＝452对应点的坐标为(22,－22),而2004＝2025－21,故2004对应点的坐标为(1,－22)．

4．(－13,0)或(27,0)或分类讨论,借助面积计算．

5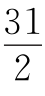．(,0)　分别过点A,D作AA′⊥OB于A′,DD′⊥OB于D′,S四边形OADC＝S△OAA′＋S梯形ADD′A′－S△CDD′＝31,S△AOB＝62,得OB＝．

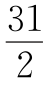6．A

7．C　连接AE,设S△ADE＝x,S△EOC＝y,则S△BDE＝x,S△AEO＝2y,S△BEC＝3y,得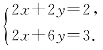

8．D

9．D　先观察横坐标与纵坐标相同的点:(0,0)粒子运动了0分钟,(1,1)粒子运动了2＝1×2分钟,(2,2)粒子运动了6＝2×3分钟,(3,3)粒子运动了12＝3×4分钟,…,(44,44)点处粒子运动了44×45＝1980分钟．这时粒子将向下运动,从而在运动了1989分钟后,粒子所在位置是(44,35)．

10．A　将棋盘上的格点(纵横线的交点)分别涂上黑、白色．规则是:①从点A开始,涂黑色;②黑白相间(与黑点相邻的是白点,与白点相邻的是黑点)．则最后点B涂黑色．显然,日字格的对角线的两端点的颜色相异．因此,马走日字格从A点到B点,所走的步数必定需奇数步,不可能是偶数．无论为奇数还是偶数,则2015n2＋2013n总是偶数,2014n＋2015与2014n3＋2015总是奇数;而2013n＋2014与n同奇偶．

所以,马走日字格从A点到B点,所走的步数不可能是偶数2015n2＋2013n．故答案选A．

11．(1)±6

(2)B点横坐标为5或－1．

(3)由方程组得c－a＝2＞0,c－b＝7＞0,

∴c＞a＞b,即点A在点B右边,点C在点A右边．

(第11题)

12．(1)A(1,1)

(2)P3(－5．2,1．2)　P8(2,3)

(3)∵P1(0,－1)→P2(2,3)→P3(－5．2,1．2)→P4(3．2,－1．2)→P5(－1．2,3．2)→P6(－2,1)→P7(0,－1)→P8(2,3)．

∴坐标以6为周期循环,而2012÷6＝335……2,故P2012的坐标与P2的坐标相同,为P2012(2,3)．

13．由题中条件,知x2＋y≠x＋y2．

假设存在两个不同整点(x,y),(x′,y′),满足

由于(x,y),(x′,y′)是两个不同整点,故在x与x′、y与y′中至少有一组中两数不等．不妨设x≠x′．

y－y′＝x′2－x2＝(x′－x)(x′＋x),

x－x′＝y′2－y2＝(y′－y)(y′＋y)．

则x－x′＝－(x′－x)(x′＋x)(y′＋y)．

因为x≠x′,所以(x′＋x)(y′＋y)＝1．

情形1:x′＋x＝y′＋y＝1．则x′＝1－x,y′＝1－y．

故x2＋y＝(1－x)2＋(1－y)．

整理得x＋y＝1．而y′＋y＝1,故x＝y′,x′＝y．

从而x2＋y＝y′2＋x′＝x＋y2,矛盾．

情形2:x′＋x＝y′＋y＝－1．

则x′＝－1－x,y′＝－1－y．

故x2＋y＝(－1－x)2＋(－1－y)．

整理得x＝y．从而x2＋y＝x＋y2,矛盾．

因此原结论成立．

14．(1)如图,过点P作PE⊥y轴于点E．因为△PAD的面积等于△POC的面积,所以3AE＝5OE,即3(8－OE)＝5OE,解得OE＝3．所以△PAD的面积＝△POC的面积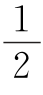＝×3×5＝7．5,△PAO的面积＝△PCD的面积＝[(3＋5)×8÷2－2×7．5]÷2＝8．5,则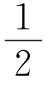×8PE＝8．5,即PE＝,所以点P的坐标是

(第14题)

(2)取O′(0,6),连接PO′,则∠POE＝∠PO′E＞∠PAE,从而90°－∠POE＜90°－∠PAE,所以∠POC＜∠PAD．

15．(1)能到达点(3,5)和点(200,6)．

从(1,1)出发到(3,5)的路径为:

(1,1)→(2,1)→(4,1)→(3,1)→(3,2)→(3,4)→(3,8)→(3,5)．

从(1,1)出发到(200,6)的路径为:

(1,1)→(1,2)→(1,4)→(1,3)→(1,6)→(2,6)→(4,6)→(8,6)→(16,6)→(10,6)→(20,6)→(40,6)→(80,6)→(160,6)→(320,6)→(前面的数反复减20次)→(200,6)．

(2)不能到达点(12,60)和(200,5)．

理由如下:

∵a和b的公共奇约数＝a和2b的公共奇约数＝2a和b的公共奇约数,

∴由规则①知,跳跃不改变前后两数的公共奇约数．

又∵如果a＞b,a和b的最大公约数＝(a－b)和b的最大公约数,

如果a＜b,a和b的最大公约数＝(b－a)和b的最大公约数,

∴由规则②知,跳跃不改变前后两数的最大公约数．

从而按规则①和规则②跳跃,均不改变坐标前后两数的公共奇约数．

∵1和1的公共奇约数为1,12和60的公共奇约数为3,200和5的公共奇约数为5．

∴从(1,1)出发不可能到达给定点(12,60)和(200,5)．

16．设(n,m)＝d,n＝ad,m＝bd,(a,b)＝1．先将棋盘分割为d×d块,每块中的d2个方格彼此同色．再以各块的中心为格点,d为边长作格点阵(每个格点代表d×d块)．

(1)若a,b一奇一偶,依国际象棋棋盘方式间隔染色,即当x＋y为偶数时将(x,y)染黑色,而x＋y为奇数时将(x,y)染白色．由于a＋b为奇数,故马(n,m)每步的起点(x,y)与终点(x±a,y±b)或(x±b,y±a)的坐标和不同奇偶,从而不同色．

(2)若a,b同为奇数,依x的奇偶间隔染色(同一x的整个竖直条同色)．同样因为每步x与x±a或x±b不同奇偶,从而起点与终点不同色．

17．在平面直角坐标系中任作一个正五边形,设其边长为a,对角线长为b．

假设五个顶点中存在三个有理点．则三点之间的距离必同时含有a与b这两个值．又两个有理点之间距离的平方为有理数,故a2、b2均为正有理数,与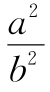为无理数矛盾．

因此,平面直角坐标系中的任意正五边形,其有理顶点的个数不大于2．这表明,其五个顶点中无理点更多．