2020精英数学大视野七年级第16讲：一元一次不等式

2025-09-29 理论教育版权反馈

【摘要】：当n＝106时,a＝46;当n＝107时,a为非整数,舍去．多元不等式通过确定主元、放缩、代入消元或运用不等式性质等方法,化多元不等式为一元不等式,是解多元不等式的重要策略．宋朝大学者朱熹曾说:“读书无疑者,须教有疑。”13．已知,求|x－1|－|x＋3|的最大值和最小值．(北京市“迎春杯”竞赛题

用不同的元素(如字母或颜色)填入幻方,使该元素每行每列都只出现一次．这是瑞士大数学家欧拉在晚年构造的“拉丁幻方”．拉丁幻方既可训练思维,又能帮助人们设计实验方案．

知能概述

不等式是探求不等关系的基本工具．不等式与方程在相关概念、性质、解法上有着相似点,类比是学习不等式的重要方法．

解含字母系数的不等式、绝对值不等式常用到分类讨论法．

确定不等式中参数的取值范围,需逆用不等式解集、借助数轴．

问题解决

例1　如果关于x的不等式(2m－n)x－m－5n＞0的解集为x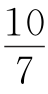＜ pagenumber_ebook=143,pagenumber_book=137 ,那么,关于x的不等式mx＞n(m≠0)的解集为________．

(黑龙江省哈尔滨市竞赛题)

解题思路　从已知条件出发,解关于x的不等式,求出m,n的值或m,n的关系．

例2　如果关于x的不等式组的整数解仅为1,2,3,那么适合这个不等式组的整数对(m,n)共有(　)．

A．49对　B．42对　C．36对　D．13对

(江苏省竞赛题)

即使在数学里,发现真理的主要工具也是类比．

——拉普拉斯

类　比

若两个对象在某些方面有相同的性质,则推测它们在其他方面也可能有相同的性质,这样的思考方法叫类比．

光和声,在许多方面有相同的性质．如它们都是直线传播,都有折射与反射现象等．根据声的波动性质,荷兰物理学家、数学家惠更斯(1629—1695)得出“光可能有波动的性质”的猜想．后来,光的波动性质通过实验得到了验证．

解题思路　借助数轴,分别建立m,n的不等式,确定整数m,n的值．

例3　解下列关于x的不等式:

(1)(2mx＋3)－n＜3x;

(2)|x－2|≤2x－10;

(3)|x－5|－|2x＋3|＜1．

(上海市竞赛题)

解题思路　与方程类似,解含字母系数的不等式需要对字母系数进行讨论;解绝对值不等式的关键是去掉绝对值符号,化为一般的不等式来解,需分类讨论．

例4　在a与3－2a之间(不包括这两个数)有且只有一个整数,求实数a的取值范围．

(“希望杯”邀请赛试题)

解题思路　解含参数不等式组的整数解问题,一般需确定整数解,而本例条件只知整数解的个数,恰当换元,可降低问题的难度．

例5　已知三个非负数x,y,z满足关系式:x＋3y＋2z＝3,3x＋3y＋z＝4．若M＝3x－2y＋4z,求M的最大值和最小值．

(山西省太原市竞赛题)

解题思路　通过解方程组,用含一个字母的式子来表示M,通过解不等式组,确定这个字母的取值范围,在约束条件下,求M的最大值和最小值．

学习不等式

(1)基本≠简单．

许多人非常不重视基本的东西,甚至轻视它,“基本”应该等于“重要”加上“简单”．

(2)懂≠会≠对．

“懂”有时只是表面的,只是形式上的了解,还必须经过组织与整理,融会贯通,并从问题的演练中,不断地发现自己不会的地方,才可以逐渐达到“真会”的地步．

例6　求满足下列条件的最小正整数n:对于n存在正整数k,使得成立．

(美国数学邀请赛试题)

给出下列解法,其中哪些是对的?哪些是错的?对的原理是什么?错的原因又在哪里?

故满足条件的最小正整数n＝97．

例7　将若干个由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53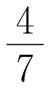 pagenumber_ebook=145,pagenumber_book=139 ,问删去的那个数是多少?

(“华罗庚杯”少年数学邀请赛试题)

当n＝106时,a＝46;当n＝107时,a为非整数,舍去．

多元不等式

通过确定主元、放缩、代入消元或运用不等式性质(若a＞b,c＞d,则a＋c＞b＋d)等方法,化多元不等式为一元不等式,是解多元不等式的重要策略．

宋朝大学者朱熹曾说:“读书无疑者,须教有疑。”明朝陈献章说:“小疑则小进,大疑则大进．疑者,觉悟之机也,一番觉悟,一番长进．”

就解题而言,解法是否正确?有没有不同解法?解法孰优孰劣等,有许多值得思考探索的空间．

“不要迷信权威,人云亦云”,这是镌刻在英国皇家学会会徽上的大义微言．

例6的更一般问题是:

若不等式

对m个整数k成立,求正整数n的最大值和最小值．

例8　已知方程组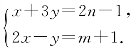 pagenumber_ebook=145,pagenumber_book=139 的解x,y满足条件:－1≤x≤1,1≤y≤2,求m,n的取值范围．

(“华罗庚金杯”少年数学邀请赛试题)(https://www.chuimin.cn)

解　解方程组得

结合x,y满足的条件,得到

由①得

由②的第一式加上第二式乘以3的积,并做简化,得到

由②的第一式可得

由②的第一式加上第④式乘以2的积,并做简化,得到

1．已知关于x的不等式(2a－b)x＋a－5b＞0的解是x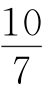＜ pagenumber_ebook=146,pagenumber_book=140 ,则ax＋b＞0的解是________．

(安徽省竞赛题)

2．已知关于x的不等式组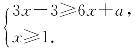 pagenumber_ebook=146,pagenumber_book=140 的解是1≤x≤3,则a＝_________．

(四川省竞赛题)

3．若关于x的不等式|x－a|＋|x－12|＜6对于任意实数x均不成立,则实数a的取值范围是_________．

(天津市竞赛题)

4．若关于x的不等式1－|x|＞ax的解集中有无穷多个整数,则a的取值范围是________．

(上海市“宇振杯”竞赛题)

相等与不等是矛盾的两个方面,既相互统一,又可以互相转化,具体体现在:

(1)运用不等式(组)讨论方程(组)的解的正负性;

(2)运用不等式(组),用逼近的方法求特殊方程(组)的解;

(3)对于含有等式、不等式的混合型问题,综合运用方程(组)(消元思想)不等式(组)(逼近方法)求解．

5．若正整数a,b满足,且a＋b最小,则a＝________,b＝________．

(“希望杯”邀请赛试题)

6．已知非负数a,b,c,d,e满足等式a＋b＋c＋d＋e＝1,若a＋b＋c,b＋c＋d,c＋d＋e的最大值为M,则M的最小值为(　)．

(“华罗庚金杯”少年数学邀请赛试题)

10．已知x,y,z是三个非负数,且满足3x＋2y＋z＝5,x＋y－z＝2．若S＝2x＋y－z,则S的最大值与最小值的和为(　)．

A．5　B．6　C．7　D．8

(天津市竞赛题)

11．解下列关于x的不等式

(1)|ax－1|＞ax－1;

(2)|3x＋2|－|x－6|＞1．

(广西壮族自治区竞赛题)

12．已知关于x的不等式组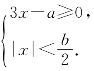 pagenumber_ebook=147,pagenumber_book=141 的整数解有且仅有4个:－1,0,1,2,那么,适合这个不等式组的所有可能的整数对(a,b)共有多少个?

(江苏省竞赛题)

13．已知,求|x－1|－|x＋3|的最大值和最小值．

(北京市“迎春杯”竞赛题)

14．已知n,k皆为自然数,且1＜k＜n,若＝10,n＋k＝a,求a的值．

(香港中学生数学竞赛题)

15．求最大的正整数n,使不等式对唯一的一个整数k成立．

(“希望杯”邀请赛试题)

16．设x1,x2,x3,x4,x5,x6,x7是自然数,且x1＜x2＜x3＜x4＜x5＜x6＜x7,x1＋x2＝x3,x2＋x3＝x4,x3＋x4＝x5,x4＋x5＝x6,x5＋x6＝x7．又x1＋x2＋x3＋x4＋x5＋x6＋x7＝2010．求x1＋x2＋x3的最大值．

(“希望杯”邀请赛试题)

17．已知关于x的不等式组 pagenumber_ebook=148,pagenumber_book=142 的解集中的整数恰好有两个,求实数a的取值范围．

(天津市竞赛题)

18．是否存在c满足:对任意的有理数a,b都有|a＋b|,|a－b|,|1－b|三个值中最大值大于等于c?如果存在这样的c,请给出一个具体的数值,并求c的最大值;如果不存在,请说明理由．

(“华罗庚金杯”少年数学邀请赛试题)

故原不等式的解集为x＜－7或x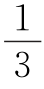＞ pagenumber_ebook=149,pagenumber_book=143 ．

例4　令a＝1＋x,则3－2a＝1－2x．

将问题转化为在1＋x与1－2x之间(不包括这两个数)有且只有一个整数,显然x≠0,容易看出这两个数在数轴上分居1的两侧．

1．x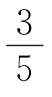＜－ pagenumber_ebook=149,pagenumber_book=143 2．－12

3．a≤6或a≥18　由已知得12－a≥6或a－12≥6．

4．a≤－1或a≥1　若x≥0,则(a＋1)x＜1,当a＋1＞0时,0≤x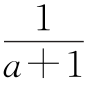＜ pagenumber_ebook=149,pagenumber_book=143 ,解集中的整数个数有限;当a＋1＜0,x＞,解集中有无穷多个整数;当a＋1＝0时,不等式显然成立,故a≤－1．若x＜0,则(a－1)x＜1,当a－1＞0,x＜,解集中有无穷多个整数;当a－1＜0时,＜x＜0,解集中的整数个数有限;当a－1＝0时,不等式显然成立,故a≥1．综上所述,a的取值范围为a≤－1或a≥1．

2020精英数学大视野七年级第16讲：一元一次不等式

相关推荐