不定方程(组)解题方法

斐波那契(约1170—约1240),意大利数学家．1202年写成名著《算盘书》,该书系统地介绍了印度—阿拉伯数码．《算盘书》在1228年的修订中增加了脍炙人口的“兔子问题”,产生了一个数列:1,1,2,3,5,8,13,21,34,55,89,…,这就是著名的斐波那契数列．

知能概述

不定方程是指未知数的个数多于方程的个数的方程,其特点是解往往有无穷多个,不能唯一确定．

对于不定方程,若限定只求整数解,加上条件限制后,解就可以确定．

解不定方程,没有现成的模式、固定的方法可循,需要根据方程的特点进行恰当的变形,并灵活运用以下知识与方法:奇数偶数、整数的整除性、分离整系数、因数分解、不等分析等．

对于一般的整系数的不定方程ax＋by＝c,若能找到它的一组特解,则这个不定方程全部整数解可表示为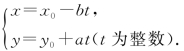

问题解决

例1　正整数m,n满足8m＋9n＝mn＋6,则m的最大值是_________．

(新加坡数学竞赛题)

解题思路　把m用含n的代数式表示,并分离其整数部分(简称分离整系数法),再利用整除知识,求出m的最大值．

解题是一种实践性技能,就像游泳、滑雪或弹钢琴一样,只能通过模仿和实践来学到它．

——波利亚

兵阵与队列

韩信点兵,多多益善．

相传韩信发号令点兵:第一次5行纵队,多出1人;第二次6行纵队,多出5人;第三次7行纵队,多出4人;第四次11行纵队,多出10人．韩信的军师很快就估算出总兵数．

例2　如图,在高速公路上从3千米处开始,每隔4千米设一个速度限制标识,而且从10千米处开始,每隔9千米设一个测速照相标识,则刚好在19千米处同时设置这两种标识．问下一个同时设置这两种标识的地点的千米数是(　)．

A．32千米　B．37千米　C．55千米　D．90千米

(河南省竞赛题)

解题思路　设设置限速标识、照相标识千米数分别表示为3＋4x,10＋9y(x,y为自然数),问题转化为求不定方程3＋4x＝10＋9y的正整数解．

例3　某中学全体师生租乘同类型客车若干辆外出春游,如果每辆车坐22人,就会余下1人;如果开走一辆空车,那么所有师生刚好平均分乘余下的汽车．问:原先租多少辆客车和学校师生共多少人?(已知每辆车的容量不多于32人)

(广西壮族自治区竞赛题)

解题思路　设原先租客车x辆,开走一辆空车后,每辆车乘坐k人,则22x＋1＝k(x－1)(23≤k≤32),解此不定方程即可．

例4　求方程的正整数解．

(“希望杯”邀请赛试题)

解题思路　易知x,y,z都大于1,不妨设1＜x≤y≤z,则,通过放缩法,将复杂的三元不定方程转化为一元不等式,通过解不等式对某个未知数的取值作出估计,逐步缩小其取值范围,求出其结果．

恰当运用不等式,利用估算或放缩的方法,寻求并缩小某个字母的取值范围,这是解复杂不定方程的常用技巧．

解不定方程组的基本方法有:

(1)视某个未知数为常数,将其他未知数用这个未知数的代数式表示;

(2)通过消元,将问题转化为不定方程求解;

(3)运用整体思想方法求解．

例5　某人家的电话号码是八位数,将前四位数组成的数与后四位数组成的数相加得14405,将前三位数组成的数与后五位数组成的数相加得16970,求此人家的电话号码．

(湖北省武汉市竞赛题)

分析与解　设此八位数为abcdefgh,为将两个已知条件变为两个方程,需进一步整体设元．设为x,为y,为z,则电话号码是100000x＋10000y＋z,其中x,y,z均为自然数,且100≤x≤999,0≤y≤9,1000≤z≤9999,由题意得

②－①,并化简得1111y－x＝285,即1111y＝x＋285．

∵100≤x≤999,∴385≤x＋285≤1284,

∴

又∵y为整数,∴y＝1,x＝826,z＝6144,

故此人家的电话号码为82616144．

例6　某城市有一段马路需要整修,这段马路的长不超过3500米,今有甲、乙、丙三个施工队,分别施工人行道、非机动车道和机动车道．他们于某天零时同时开工,每天24小时连续施工．若干天后的零时,甲完成任务;几天后的18时,乙完成任务;自乙队完成的当天零时起,再过几天后的8时,丙完成任务．已知三个施工队每天完成的施工任务分别为300米、240米、180米,问这段路面有多长?

(江苏省竞赛题)

解法1　乙队最后一天完成240×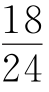＝180米,丙队最后一天完成180×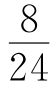＝60米．

设甲队a天完成,过b天后的18时乙队完成,自乙队完成的当天零时起,再过c天后的8时丙队完成,则

即

两式相减,得5b＋3＝3c－2,b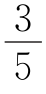＝c－1．

∵b是正整数,∴c＝5,10,15,…．

若c＝5,则b＝2,a＝11;当c≥10时,b≥5,a≥23,这时马路长超过3500米,矛盾．

故马路的长为300×11＝3300(米)．

又甲每天施工300米,若干个整天后完成任务,所以马路的长是正整数．

例5还可转化为下列数字谜问题求解．读者不妨一试．

解应用问题的关键是对问题条件的代数化．

牛顿用数学的语言、方法描述和研究自然规律,他呕心沥血写成的光辉著作《自然哲学的数学原理》,照亮了人类科学文明的大道．

牛顿在他的《普遍算术》一书中写道:“要解答一个含有数量间的抽象关系的问题,只要把题目的语言译成代数的语言就行了．”

另外三个队施工的天数虽然不知道,但知道乙队比甲队多花了若干个整天再多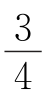天,丙队比甲队多花了若干个整天再多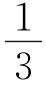天．根据这些信息,我们还可有如下的解法．

由①得　x＝1200m＋900,　③

由②得　x＝450n＋150．　④

∵x≤3500,∴m＝1,2．

当m＝1时,由③得x＝2100,由④得n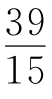＝,n不是正整数,舍去．

当m＝2时,由③得x＝3300,由④得n＝7,符合题意．

∴这段路面全长为3300米．

例7　现有质量分别为9克和13克的砝码若干只,在天平上要称出质量为3克的物体,问:至少要用多少只这样的砝码才能称出?并证明你的结论．

(山东省竞赛题)

分析　根据题意知,相同质量的砝码不会同时出现在天平的两个秤盘之中,所以可以转化为求解不定方程的问题．

解　假定当天平平衡时,用9克的砝码|x|只,当该砝码出现在被称物体所在的秤盘中时,x取负整数．同理,假定13克的砝码用了|y|只．所以当天平平衡,即称出了3克的物体时,应有9x＋13y＝3．

问题转变为在上述条件下,求|x|＋|y|的最小值．

易得x＝9,y＝－6是该方程的一组解,

∴

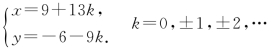
(1)当k＝0时,x＝9,y＝－6,|x|＋|y|＝15．

(2)当k≥1时,|x|≥22,|y|＞0,从而|x|＋|y|＞22．

(3)当k≤－1时,若k＝－1,则x＝－4,y＝3,|x|＋|y|＝7;

若k＜－1,则|y|≥12,|x|＞0,从而|x|＋|y|＞12．

由上述可知,至少要用7只这样的砝码,其中9克的4只,13克的3只．

例7与它的解来自不同的领域,似乎没有关联,但通过分析我们找到了它们的联系,数学中有许多这样的例子．唐代诗人王维的诗可以用来描述这一过程:

遥爱云木秀,

初疑路不同．

安知清流转,

偶与前山通．

分离整系数

类似于假分数的化简,当分子的次数大于或等于分母的次数时,通过除法,我们可以把一个分式化为整式部分与分式部分的和．

例8　小强在银行兑换了一张面值为100元以内的人民币支票,兑换员不小心将支票上的元与角、分数字看倒置了(例如把20．13元看成13．20元),并按看错的数字支付．小强将其款花去了3．50元后,发现其余额恰为支票面额的2倍,于是急忙到银行将多领的款项退回,那么小强应退回的款额是多少元?

(“中环杯”竞赛题)

解法1　设支票上原有的元与角、分数字分别为x和y,则(100y＋x)－350＝2(100x＋y),其中x,y为整数,且0≤x＜100,0≤y＜100,

故小强支票面额为14．32元,误看成32．14元,应退32．14－14．32＝17．82元．

故小强支票面额为14．32元,误看成32．14元．

应退32．14－14．32＝17．82元．

在数学领域中,数论的风格极为独特．数论是人类知识最古老的一个分支,然而它的一些最深奥的秘密与其最平凡的真理是密切相连的．

著名物理学家麦克斯韦说:“可以说是数统治着整个量的世界,而算术的四则运算可以看作是数学家的全部装备．”

1．若正整数a,b,c满足a＋2bc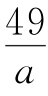＝, 则a＋b＋c的最大值是________．

(“希望杯”邀请赛试题)

2．有5克、25克、30克、50克的砝码各若干个,从中共取n个,每类砝码至少取1个,50克的砝码不能超过6个,若总重为1千克,则n的最小值为________．

(世界数学团体锦标赛试题)

3．小明某天在文具店做志愿者卖笔,铅笔每支售4元,圆珠笔每支售7元,开始时他有铅笔和圆珠笔共350支．当天虽然没有全部卖完,但是他的销售收入恰好是2013元,则他至少卖出了_________支圆珠笔．

(全国初中数学竞赛题)

4．顺思逆想

一年共有12个月,闰年的2月是29天,又有4个小月,7个大月,所以闰年共有29×1＋30×4＋31×7＝366(天)．反过来思考:如果非负整数a,b,c满足等式:29a＋30b＋31c＝366,那么a＋b＋c＝________,这样的数组(a,b,c)共有________组,它们分别是________．

(《时代学习报》数学文化节试题)

5．(中国古代数学问题)唐太宗传令点兵,若一千零一卒为一营,则剩一人;若一千零二卒为一营,则剩四人．此次点兵至少有________人．

(“希望杯”邀请赛试题)

6．一辆客车、一辆货车和一辆轿车在一条笔直的公路上朝同一方向匀速行驶．在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间．过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;再过t分钟,货车追上了客车,则t＝_________．

(《数学周报》杯全国竞赛题)

7．甲和乙每人都有若干面值为整数元的人民币．甲对乙说:“你若给我2元,我的钱数将是你的n倍．”乙对甲说:“你若给我n元,我的钱数将是你的2倍．”其中n为正整数,则n的可能值的个数是(　)．

A．1　B．2　C．3　D．4

(全国初中数学竞赛题)

8．若正整数a,b,c满足＝1,则这样的正整数组(a,b,c)共有(　)组．

A．1　B．3　C．9　D．10

(“希望杯”邀请赛试题)

9．今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分．在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有(　)．

A．2种　B．3种　C．4种　D．5种

(黑龙江省中考题)

10．电影票有10元、15元、20元三种票价,班长用500元买了30张电影票,其中票价为20元的比票价为10元的多(　)．

A．20张　B．15张　C．10张　D．5张

(“希望杯”邀请赛试题)

11．甲、乙、丙、丁四种商品的单价分别为2元、3元、5元和7元,现从中选购了6件,共花费36元．如果至少选购了3种商品,则购买了(　)件丁商品．

A．1　B．2　C．3　D．4

(“华罗庚金杯”少年数学邀请赛试题)

12．设A,B,C,D是四个小于10的不同的自然数,且满足

则D有(　)个不同的值．

A．2　B．4　C．7　D．8　E．9

(美国数学竞赛题)

13．一个盒子里装有不多于200粒棋子,如果每次2粒、3粒、4粒或6粒地取出,最终盒内都剩1粒棋子;如果每次11粒地取出,那么正好取完,求盒子里共有多少粒棋子．

(重庆市竞赛题)

14．将一个三位数的中间数码去掉,成为一个两位数,且满足＝9(如155＝9×15＋4×5),试求出所有这样的三位数．

(山西省太原市竞赛题)

15．在打靶中,某运动员每发都是命中8、9或10环,他打了多于11发的子弹,共得100环．问:该运动员共打了几发以及命中情况如何?

(俄罗斯中学生数学竞赛题)

16．将2到10这9个自然数填入如图中的9个圆圈中,每个数只能用一次,且使每一条直线上的三个数的和相同．求中间圆圈所填的数．

(第16题)

(世界数学团体锦标赛试题)

17．已知正整数x,y满足＝a(a为自然数,且x＜y),求x和y．

(江西省南昌市竞赛题)

18．从四个数中任取两个不同数求和,得到的和分别为189,320,287,234,x,y,求x＋y的最大值．

(美国数学竞赛题)

19．某单位职工参加市工会组织的健身操比赛进行列队,已知6人一列少2人,5人一列多2人,4人一列不多不少,请问这个单位参加健身操比赛的职工至少有几人?

(河南省竞赛题)

20．没有放上的数字

精密的计算与严密的推理是数学有别于其他学科的最显著特点．下面的问题是美国著名数学家乔治·萨默斯在他的著作《测试你的逻辑推理能力》中向我们提出的50道推理趣题中的一道,原题题目是“没有放上的数字”．

如图,把0～9这10个数字中的9个数字分别放在三角形周边的9个字母的位置上,使得三角形各边上的4个数字之和均为14．

解题思路　9个字母,10个数字,单靠试凑,要找出所有可能的解,几乎是不可能的．故需先进行分析,再运用逻辑推理,缩小范围,然后讨论,并辅以试凑,方能解决．

(第20题)

1．26　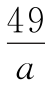是正整数,a＝1,7和49．

2．31

3．207　设小明卖出铅笔x支,圆珠笔y支,

则4x＋7y＝2013且x＋y＜350(x,y均为非负整数),

得x＝503－2y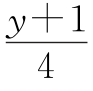＋,设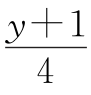＝k(k为整数),则y＝4k－1,

x＝505－7k,可求得k＞51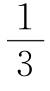,故k＝52．

4．12　4　(0,6,6),(1,4,7),(2,2,8),(3,0,9)　参见第15题．

5．1000000　设第一次点兵共x营,第二次点兵共y营,则1001x＋1＝1002y＋4,即1001(x－y)－3＝y,x－y最小值等于1,此时y＝998,至少有998×1002＋4＝1000000(人)．

6．15　设在某一时刻,货车与客车、小轿车的距离均为s千米,小轿车、货车、客车的速度分别为a千米/分、b千米/分、c千米/分,并设货车经过x分钟追上客车．则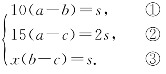

由①②,得30(b－c)＝s,所以x＝30,t＝30－10－5＝15(分钟)．

7．D　设甲、乙所有的钱数分别为x,y元(x,y为正整数),则解得2y－7的值分别为1,3,5,15,从而n的值分别为8,3,2,1．

8．D　讨论、放缩得3,3,3;4,4,2;2,3,6满足条件,由排列组合知共有1＋3＋6＝10(组)满足条件．

9．B　设小虎足球队胜了x场,平了y场,负了z场,又设踢平场数是所负场数的k倍,可得

10．C　设购买10元、15元、20元的电影票分别为x,y,z张,则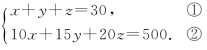

由②－①×15,得5(z－x)＝50,z－x＝10．

11．D　设甲、乙、丙、丁四种商品各选购了a、b、c、d件,

则消去d,得5a＋4b＋2c＝6,

∴a＝0或1．

当a＝1时,4b＋2c＝1无解;

当a＝0时,2b＋c＝3,得(b,c,d)＝(1,1,4),(0,3,3)(舍去)．

12．C　A＋B＝D,3＝1＋2≤A＋B＝D≤9．

所以y＝15,18,21,对应的x＝2,6,10．

如图:

(第16题)

因为b为正整数,可令m＋1＝5n,所以m＝5n－1(n是正整数),　④

将④代入③,得a＝2(5n－1)＋1＝10n－1．

∴　y＝6a－2＝6(10n－1)－2＝60n－8(n是正整数)．

当n＝1时,y有最小值52．即参加比赛列队的至少有52人．

20．2(A＋D＋G)＋(B＋C＋E＋F＋H＋I)＝14×3．

记A＋D＋G＝x,B＋C＋E＋F＋H＋I＝y,字母J代表未用上的数字．0～9这10个数字之和为45,于是得到方程组

解得x＝J－3,J＝x＋3．

由于x＝A＋D＋G≥0＋1＋2＝3,

即x≥3,于是J≥6．因此有

只有这四种情形,从而大大缩小了问题的范围．

当x＝3时,J＝6,取(0,1,2);当x＝4时,J＝7,取(0,1,3);

当x＝5时,J＝8,取(0,1,4)或(0,2,3);当x＝6时,J＝9,取(0,1,5)或(0,2,4)或(1,2,3)．

在此基础上,可确定三角形的各条边上的数字可能的填法．