解行程问题的技巧—甲、乙、丙的百米赛跑结果

七巧板是我国民间流传最久的一种拼板玩具,大约在一千年前的宋代就已经盛行,在当今被誉称为“唐图”(Tangram),意思是“中国的拼板图”．

七巧板是一种能分成7小块的正方形拼板,用它可拼成很多几何图形以及有趣的动物、人物、建筑物等．

知能概述

行程问题是最为有趣而又多变的方程应用题的一种,其三要素是距离、速度、时间．

行程问题按运动方向可分为相遇问题、追及问题;按运动路线可分为直线形问题、环形问题等,而相遇、追及是最基本的模型．

熟悉相遇问题、追及问题等基本类型的等量关系是解行程问题的基础;而恰当设元,借助直线图辅助分析,巧用比例等是解行程问题的技巧．

问题解决

例1　小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车．假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间x发一辆车,那么,发车间隔的时间x是_________分钟．

(《数学周报》杯全国初中数学竞赛题)

解题思路　本题包含了行程问题中的相遇与追及两种情况．设汽车的速度为a米/分,小王速度为b米/分,则当一辆汽车追上小王时,另一辆汽车在小王后面ax米处,它用6分钟追上小王;又当一辆汽车与小王相遇时,另一辆汽车在小王前面ax米处,它经过3分钟与小王相遇,由此布列方程．

掌握数学就意味着善于解题．

——波利亚

平均速度

1937年秋,科学巨匠爱因斯坦收到一封来信,朋友在信的末尾给他出了一道有趣的数学题:一辆老破车要翻过一座山,上山、下山的路程各为1英里,它上山时的速度小于每小时15英里,问:下山的速度要多快,才能使平均速度达到每小时30英里?

例2　如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A……方向,甲从A以65米/分的速度行走,乙从B以72米/分的速度行走,当乙第一次追上甲时在正方形的(　)．

A．AB边上　B．DA边上　C．BC边上　D．CD边上

(安徽省竞赛题)

解题思路　本例是一个特殊的环形的追及问题,注意甲实际在乙的前面3×90＝270(米)处．

例3　父亲和儿子在100米的跑道上进行赛跑,已知儿子跑5步的时间父亲能跑6步,儿子跑7步的距离与父亲跑4步的距离相等．现在儿子站在100米跑道的中点处,父亲站在100米跑道的起点处同时开始跑．问:父亲能否在100米的终点处超过儿子?并说明理由．

(重庆市竞赛题)

解题思路　把问题转化为追及问题,即比较父亲追上儿子时,儿子跑的路程与50米的大小,为了理顺步长、路程的关系,需增设未知数,这是解题的关键．

例4　甲、乙二人在同一条椭圆形跑道上作特殊训练:他们同时从同一地点出发,沿相反方向跑,每人跑完第一圈到达出发点后立即回头加速跑第二圈．跑第一圈时,乙的速度是甲速度的,甲跑第二圈的速度比第一圈提高了,乙跑第二圈时速度提高了,已知甲、乙二人第二次相遇点距第一次相遇点190米．问:这条椭圆形跑道长多少米?

(“华罗庚金杯”少年数学邀请赛试题)

解题思路　设跑道长s米,甲跑第一圈的速度是每分钟v米,把两次相遇时甲距出发点的距离分别用s的代数式表示．

例3是下面古代问题的拓展．

马跑5步的时间狗跑6步,狗跑4步的距离与马跑7步的距离相等．马已跑出5．5千米时,狗开始追它,马再跑多远,狗可追上马?

解题的关键是马与狗的速度之间关系的分析．

若两人同时相向而行,则从开始到相遇:

(1)所用时间相等,这是一个隐含的等量关系;

(2)所走的路程之比等于速度之比,这是解行程问题的一个技巧,俗称“比例法”．

例5　甲、乙、丙三人一起进行百米赛跑(假定三人均为匀速直线运动),如果当甲到达终点时,乙距终点还有5米,丙距终点还有10米,那么,当乙到达终点时,丙距终点还有多少米?

(北京市“迎春杯”竞赛题)

解题思路　为建立方程,需增设甲、乙分别跑完全程所需时间及乙、丙的速度．

例6　甲、乙二人分别从A,B两地同时出发,在距离B地6千米处相遇,相遇后两人又再继续按原方向、原速度前进,当他们分别到达B地、A地后,立刻返回,又在距A地4千米处相遇,则A,B两地相距多少千米?

(“祖冲之杯”邀请赛试题)

解法1　第一次相遇时,甲、乙两人所走的路程之和,正是A,B两地相距的路程,即当甲、乙合走完A,B间的全部路程时,乙走了6千米．第二次相遇时,两人合走的路程恰为两地间距离的3倍(如图,图中实线表示甲所走路线,虚线表示乙所走路线),因此,这时乙走的路程应为6×3＝18(千米)．考虑到乙从B地走到A后又返回了4千米,所以A,B两地间的距离为18－4＝14(千米)．

解法2　甲、乙二人同时动身,相向而行,到相遇时二人所走时间相等,又因为二人都做匀速运动,应有:二人速度之比等于他们所走路程之比,且相同时间走过的路程亦成正比例．

到第一次相遇,甲走了(全程－6)千米,乙走了6千米;

到第二次相遇,甲走了(2×全程－4)千米,乙走了(全程＋4)千米．

设全程为s,易得到下列方程,

解之,得s1＝14,s2＝0(舍去),

所以A,B两地相距14千米．

例6似乎缺少条件,充分运用“同时”“匀速”“两次相遇”等隐含的条件,就为解题铺平了道路,解法1是算术法,解法2是比例法,解法3是增设辅助未知数．

一题多解,沟通了知识的联系,揭示了问题的深层结构．

需要注意的是,算术法有自身的优点,是学习数论与组合数学的基础,不能因学习代数方法,而将算术法完全摒弃．

解法3　设全程为s千米,甲、乙二人速度分别为v1,v2．则

①÷②,得,

解得s＝14或s＝0(舍去)．

例7　8个人乘速度相同的两辆小汽车同时赶往火车站,每辆车乘4人(不包括司机),其中一辆小汽车在距火车站15千米的地方出现故障,此时,距停止检票的时间还有42分钟,这时,唯一可利用的交通工具是另一辆小汽车,已知包括司机在内这辆车限乘5人,且这辆车的平均速度是60千米/时,人步行的平均速度是5千米/时,试设计两种方案,通过计算说明这8个人能够在停止检票前赶到火车站．

(全国初中数学竞赛题)

分析与解　有以下设计方案:(1)当小汽车出现故障时,乘这辆车的4个人下车步行,另一辆车将车内的4个人送到火车站,立即返回接步行的4个人到火车站;(2)当小汽车出现故障时,乘这辆车的4个人先下车步行,另一辆车将车内的4个人送到某地方后,让他们下车步行,再立即返回接因汽车出现故障而步行的另外4个人,使得两批人员最后同时到达车站．

环形运动

环形运动是一种在封闭的状态下进行的特殊运动．若同向运动时,则是一个追及问题;若反向运动时,则是一个相遇问题．

化圆为直,化陌生为熟悉,运用直线图分析环形运动这是解相关问题的本质的策略．

例8　如图,已知一周长为30cm的圆形轨道上有相距10cm的A,B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长)．动点P从A点出发,以acm/s的速度,在轨道上按逆时针方向运动;与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动．设运动时间为t(s),当t＝5时,动点P,Q第一次相遇．

人车同时出发,若人车同时到达目的地,则时间最短,而关键在于平等地使用交通工具,这样乘车路程相等、步行路程也相等,这是隐含的等量关系．

“俱怀逸兴壮思飞,欲上青天揽明月．”

1894年,匈牙利教育部组织了第一届中学生数学竞赛,这是真正数学竞赛的开端．数学竞赛为匈牙利造就了一大批世界著名学者．计算机之父冯·诺伊曼、原子弹之父泰勒、航天之父冯·卡门、波利亚等都是数学竞赛的优胜者．

(1)求a的值;

(2)若a＞3,则在P,Q第二次相遇前,当动点P,Q在轨道上相距12cm时,求t的值．

解题思路　化圆为直,由直线图中的线段关系布列方程．“P,Q第二次相遇前”是怎样的含义?故全面讨论是解题的关键．

1．如图,正方形ABCD的周长为40m,甲、乙两人分别从A,B同时出发,沿正方形边行走,甲按逆时针方向每分钟行35m,乙按顺时针方向每分钟行30m．如果记号(a,b)表示两人出发后已行了amin,并相遇过b次,那么,当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是_________．

(第1题)

(江苏省竞赛题)

2．在一条笔直的公路上,某一时刻,有一辆客车在前,一辆小轿车在后,一辆货车在客车与小轿车的正中间同向行驶．过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;此后,再过t分钟,货车追上了客车,则t＝_________．

(“希望杯”邀请赛试题)

3．点A,B,C是一条直路上依次排列的三点,其中A与C相距1800米．艾娜的速度是伊芙的两倍,保罗的速度是艾娜的两倍．三人同时出发,其中艾娜从A跑向C,保罗从B跑向C,伊芙从C跑向A．当保罗与伊芙相遇时,保罗调头跑向A,然后保罗与艾娜恰好在B点相遇,则A到B的距离为________．

(美国数学竞赛题)

4．甲、乙两个同学从A地到B地,甲步行的速度为每小时3千米,乙步行的速度为每小时5千米,两人骑自行车的速度都是每小时15千米．现在甲先步行,乙先骑自行车,两人同时出发,走了一段路程后,乙放下车步行,甲走到乙放车处改骑自行车,以后不断交替行进,两人恰好同时到达B地,甲走完全程的平均速度是________千米/小时．

(“华罗庚金杯”少年数学邀请赛试题)

爱因斯坦质能方程E＝mc2被称为“最有名的方程”,奠定了原子理论的基础．

5．甲、乙两个机器人同时按匀速进行100米跑道测试,自动记录仪显示:当甲距离终点1米时,乙距离终点2米;当甲到达终点时,乙距离终点1．01米．经过计算,这条跑道长度不标准．则这条跑道比100米多了________米．

(江西省南昌市竞赛题)

6．某段公路由上坡、平坡、下坡三个等长的路段组成,已知一辆汽车在三个路段上行驶的平均速度分别为v1,v2,v3,则该汽车在这段公路上行驶的平均速度为(　)．

(天津市竞赛题)

7．甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点……若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后100s内,两人相遇的次数为(　)．

A．3　B．4　C．5　D．6

(浙江省台州市中考题)

8．甲乙两人同时从A地出发沿同一条线路去B地,若甲用一半的时间以a千米/时的速度行走,另一半时间以b千米/时的速度行走;而乙用a千米/时的速度走了一半的路程,另一半的路程以b千米/时的速度行走(a≠b),则(　)．

A．甲先到达B地　B．乙先到达B地

C．甲、乙同时到达B地　D．甲、乙谁先到达不能确定

(天津市竞赛题)

9．如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2007次相遇在边(　)上．

A．AB　B．BC

C．CD　D．DA

(第9题)

(湖北省黄冈市竞赛题)

10．甲、乙两人沿同一路线从A站骑车(匀速)到B站,甲要用30分钟,乙要用40分钟．如果乙比甲早出发5分钟去B站,则甲追上乙时,是甲出发后的第(　)．

A．12分钟　B．13分钟　C．14分钟　D．15分钟

(“希望杯”邀请赛试题)

11．甲、乙、丙三辆车都匀速从A地驶往B地．乙车比丙车晚5分钟出发,出发后40分钟追上丙车;甲车比乙车晚20分钟出发,出发后100分钟追上丙车,问:甲车出发后多少分钟追上乙车?

(全国初中数学竞赛题)

12．老师带着两名学生到离学校33千米远的博物馆参观．老师乘一辆摩托车,速度为25千米/时,这辆摩托车后座可带一名学生,带人后速度为20千米/时,学生步行的速度为5千米/时．请你设计一种方案,使师生三人同时出发后都到达博物馆的时间不超过3个小时．

(“希望杯”邀请赛试题)

13．如图,甲、乙、丙是三个站,乙站到甲、丙两站的距离相等．小明和小强分别从甲、丙两站同时出发相向而行,小明过乙站100米后与小强相遇,然后两人又继续前进,小明走到丙站立即返回,经过乙站后300米又追上小强,问:甲、丙两站的距离是多少米?

(第13题)

(“华罗庚金杯”少年数学邀请赛试题)

14．甲、乙两车从A向B行驶,甲比乙晚出发6小时,开始时甲、乙的速度比是4∶3．甲出发6小时后,速度提高1倍,甲、乙两车同时到达B．问:甲从A到B共走了多少小时?

(“希望杯”邀请赛试题)

15．A,B两地相距13．5千米,甲、乙两人分别从A,B同时出发,各在A,B间往返一次,甲比乙先回到出发地,两人第一次在C地迎面相遇,第二次在D地迎面相遇,从出发到两人第二次相遇经过的时间为3小时20分钟,若C,D两地相距3千米,求甲、乙两人的速度．

(“希望杯”邀请赛试题)

16．一只野兔从树林里跑出,并沿直线方向奔向一片多刺的灌木林．在到达灌木林的中途,野兔突然碰上荆棘,跑的速度减慢到原来的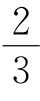．当兔子跑到距离灌木林还有50米时,一只狼从树林同一地点跑出,来追赶兔子．当兔子跑到灌木林时,狼离它还有10米．如果已知狼总是以兔子开始时的速度奔跑,试问从树林到灌木林的距离是多少米?

(莫斯科大学数学力学系入学考试题)

例8　(1)a＝1或a＝7．

(2)①在第一次相遇前,如图①,刚开始不久,3t＋12＝10＋7t,t＝0．5．

②如图②,第一次相遇前,A在B后面,相距20cm的追及模型,7t＋12＝3t＋20,t＝2．

③如图③,第一次相遇后,也就是在5秒后,又过了t秒,这时快的点P在前面,

7t－3t＝12,t＝3,5＋3＝8．

④如图④,在5秒后,又过了t秒,可以理解为相距30cm的追及模型,A在后面．

30＋3t＝7t＋12,4t＝18,t＝4．5,5＋4．5＝9．5．

故t＝0．5,2,8或9．5．

(例8)

1．(6,10)　出发后每2分钟出现一次两人同时到达顶点,当a＝b时,甲在B点,乙在D点．两人第一次相遇是在所行路程之和为10m时(AB边上),以后每当行程之和达到40m,又相遇一次,而6min两人行程之和为390m,故

2．15　设在某一时刻货车与客车、小轿车的距离均为s千米,小轿车、货车、客车的速度分别为a,b,c千米/分,由题意知,从货车在客车和小轿车的正中间,到货车追上客车共需10＋5＋t＝(15＋t)(分),于是

10(a－b)＝s,　①

15(a－c)＝2s,　②

(15＋t)(b－c)＝s．　③

由①、②得30(b－c)＝s,代入③得15＋t＝30,故t＝15．

9．C　甲、乙第一次相遇在AD边上,第二次相遇在DC边上,第三次相遇在C点,第四次相遇在BC边上,第五次相遇在AB边上,第六次相遇在AD边上的第一次相遇处．因2007÷5＝401……2,故第2007次相遇在边DC上．

10．D

11．设甲、乙、丙三车的速度分别为每分钟x,y,z米,由题意知,45z＝40y,125z＝100x．

消去z,得y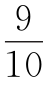＝x．

设甲车出发后t分钟追上乙车,则tx＝(t＋20)y,即tx＝(t＋20)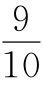x．解得t＝180．

12．要使师生三人都到达博物馆的时间尽可能短,可设计方案如下:

设学生为甲、乙二人,乙先步行,老师带甲乘摩托车行驶一定路程后,让甲步行,老师返回接乙,然后老师带乙乘车,与步行的甲同时到达博物馆．

设老师带甲乘摩托车行驶了x千米,用了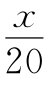小时,比乙多行了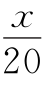×(20－5)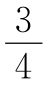＝x(千米)．

(第12题)

这时老师让甲步行前进,而自己返回接乙,遇到乙时,用了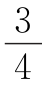x÷(25＋5)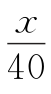＝(小时)．

乙遇到老师时,已经步行了,离博物馆还有33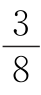－x(千米)．

要使师生三人能同时到达博物馆,甲、乙二人搭乘摩托车的路程应相同,则有x＝33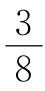－x,解得x＝24．

即甲先乘摩托车行24千米,用时1．2小时,再步行9千米,用时1．8小时,共计3小时．

因此,上述方案可使师生三人同时出发后都到达博物馆的时间不超过3个小时．

15．如图所示,第一次在C地相遇时,甲、乙两人所走过的路程和为AB,其中甲走过的路程为AC;第二次在D地相遇时,甲、乙两人所走过的路程和为3AB,其中甲走过的路程为AB＋BD．

由于甲比乙的速度快,所以D在C的左面,且有AB＋BD＝3AC,设AD＝x千米,则有13．5＋(13．5－x)＝3(x＋3),

(第15题)

解得x＝4．5,

则AC＝x＋3＝7．5(千米),BC＝13．5－7．5＝6(千米)．

所以V甲∶V乙＝7．5∶6＝5∶4

设V甲＝5a千米/时,则V乙＝4a千米/时,从出发到两人第二次相遇时用了3小时20分钟,即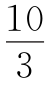小时,两人共走了3AB＝3×13．5＝40．5(千米)．

所以(V甲＋V乙)×＝40．5,

即5a＋4a＝12．15,　a＝1．35．

故V甲＝5a＝6．75(千米/时),V乙＝4a＝5．4(千米/时)．

16．以s表示从树林到灌木林的距离(米),以v表示兔子原来的速度(米/分钟)．狼追赶兔子的速度也是v(米/分钟)．可能有2种情形．