怎样设元，解题思路与示例

《九章算术》成书于公元1世纪初,全书运用问题集形式,列为九章,共246问,标志着中国古代数学体系已经形成．在世界数学史上,《九章算术》最早记载、最先使用“负数概念及正负数的运算”“线性方程组的解法”“开平方、开立方的方法”等．

知能概述

列方程解应用题是从具体问题中抽象归纳出所需要的数量关系,根据数量间的关系,依照题意合理选择未知数,找出隐含的等量关系,列方程进行求解．

恰当地设元是列方程解应用题的关键步骤之一,怎样设元,需要根据具体问题的条件来确定．

设元的基本方法有:直接设元、间接设元、辅助设元、整体设元等．

有些应用题中隐含一些未知的常量,如若不指明这些量的存在,则难求其解．故需把这些未知的常量设为参数,以便列方程,称此为辅助设元．

问题解决

例1　(1)某编辑用0～9这10个数字给一本书的各页标上页码,若共写了636个数字,则该书有_________页．

(天津市竞赛题)

(2)一个六位数的3倍等于,则这个六位数为_________．

(黑龙江省竞赛题)

解题思路　对于(1),该书页码的数字组成有三种:一个数字、两个数字、三个数字,可直接设元;对于(2),视为整体,整体设元．

与其说学习数学,倒不如说学习数学化．

——弗赖登塔尔

优与劣

算术法解应用题与列方程解应用题的共同点是都要在理解题意的基础上分析数量关系,都需要根据四则运算的意义．列方程解应用题,提供了一般的解题步骤和规范的计算方法,将逆向思考转化为顺向思考,这是列方程解应用题的优越性．

例2　植树节时,某班平均每人植树6棵;如果只由女生完成,每人应植树15棵;如果只由男生完成,每人应植树(　)棵．

A．9　B．10　C．12　D．14

(四川省竞赛题)

解题思路　本例可间接设元,如设出植树总数或班上共有人数;亦可设出辅助未知数,即分别设出男、女学生人数．

例3　某商场经销一种商品,由于进货时价格比原进价降低了6．4%,使得利润率增加了8个百分点,求经销这种商品原来的利润率．

(全国初中数学联赛试题)

解题思路　因售出价＝进货价×(1＋利润率),故还需设出进货价,利用售出价不变,辅助建立方程．

例4　10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉他两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来,若报出的数如图所示,那么报3的人心里想的数是多少?

(《数学周报》杯全国初中数学竞赛题)

解题思路　设报3的人心里想的数是x,分别把报7,9,1的人心里想的数用x的代数式表示．

例5　某大型超市元旦假期举行促销活动．规定一次购物不超过100元的不给优惠,超过100元而不超过300元时,按该次购物金额9折优惠,超过300元的其中300元仍按9折优惠,超过部分按8折优惠．小美两次购物分别用了94．5元和282．8元,现小丽决定一次购买小美分两次购买的同样的物品,那么,小丽应该付款多少元?

(海南省竞赛题)

辅助未知数的引入,在已知条件与所求结论之间架起了一座“桥梁”,对这种辅助未知量,并不能或不需求出,可以在解题中相消或相约,这就是常说的“设而不求”．

一些应用题是以一段生活实际情形、一个鲜为人知的故事或一场趣味游戏编制的,寓数学思想和方法于情境中,这类应用题被称为情境应用题．

解情境应用题的关键是:在阅读理解的基础上,取舍信息,从不同的思维角度提出问题、分析问题、恰当地理解和应用数学知识,历经有价值的数学思维活动过程．

解题思路　先求出小美第二次购物的原价．

例6　物尽其用　自行车轮胎,安装在后轮上,只能行驶3000km就要报废,安装在前轮上,则行驶5000km才报废．为使一对轮胎能在行驶尽可能多的路程后才报废,在自行车行驶一定路程后,就将前后轮胎调整,这样安装在自行车上的一对轮胎最多可行驶多少千米?

(《时代学习报》数学文化节试题)

解法1　列方程求解

设自行车行驶了xkm后,互换前、后轮胎再行驶,致使两只轮胎同时报废．因此,前轮胎还可行驶(5000－x)km,后轮胎还可行驶(3000－x)km．当前后轮胎互换后,还可行驶,并有

解此方程,有x＝2000,解得x＝1875(km)．这就是说,当自行车行驶了1875km后,互换前后轮胎,这样还可行驶(5000－1875)×＝1875(km),所以最多可行驶3750km．

解法2　类似工程问题解法

设安装在自行车上的一对轮胎最多可行驶xkm,根据题意,自行车每行驶1km,前轮胎将磨损,后轮胎将磨损,当两个轮胎磨损之和为单位“1”时,前后轮胎互换,当两个轮胎磨损之和为单位“2”时,两个轮胎同时报废,即此时行驶路程最多．由此可得方程:＝2,解得x＝3750(km)．

即自行车最多可行驶3750km．

牛吃草问题

牛顿(1643—1727)是17世纪英国著名科学家,与高斯、阿基米德被称为人类历史上最杰出的数学家．下面的问题是牛顿在他的《普通算术》一书中提出的,被称为牛吃草问题或消长问题．

人类在认识世界的过程中,学会了用抽象、简洁的方程式来描述规律,无数的方程展现了人们破解物质运动、光电闪耀、时空变幻等自然现象的曲折经历,彰显了人类百折不挠的探索精神．

例7　牧场长满一片青草,每日生长一样快,放牧27头牛,6星期吃完;放牧23头牛,9星期吃完．问:放牧21头牛,几星期吃完?

解题思路　草总量、新长草量以及剩余草量都随牛吃的天数不断变化,解题的关键是从变化中找出不变量,并理顺草每天的增长量、每头牛每天的吃草量及牧场原有的草量之间的关系．

许多数学问题形异而质同,即虽情境不同,但结构上常有相似之处,通过类比、熟悉化原则、模式识别等策略,能促使问题转化,解法2把原问题转化为一个工程问题,通俗而简捷．

对于例6,自行车在换胎前后行驶的路程相等(都是1875km),是巧合,还是隐含的规律?由此可得到其他解法,读者不妨一试．

从现实生活或者具体情境中抽象出数学问题,是建立模型的出发点;用符号表示数量关系和变化规律,是建立模型的过程;求出模型的结果并讨论结果的意义,是求解模型的过程．

例7之所以为一道名题,是因为可生成许多形异而质同的问题．

1．已知四个数的和为64,若第一个数加3,第二个数减3,第三个数乘以3,第四个数除以3,所得的结果均相同,则这相同的结果是________．

(上海市竞赛题)

2．某班全班学生进行了一次篮球投篮练习,每人投球10个,每投进一个球得1分,得分的部分情况如下表所示:

已知该班学生中,至少得3分的人平均得分为6分,得分不到8分的人的平均得分为3分,那么该班学生有_________人．

(江苏省竞赛题)

3．甲、乙两名打字员,甲每页打500字,乙每页打600字,已知甲每完成8页,乙恰能完成7页．若甲打完2页后,乙开始打字,则当甲、乙打的字数相同时,乙打了________页．

(“希望杯”邀请赛试题)

4．从两个质量分别为12千克和8千克且含铜量的百分比不同的合金上切下重量相等的两块,把所切下的每一块和另一块剩余的合金放在一起熔炼后得到的两块合金含铜的百分数相等．则所切下的每块合金的重量是_________千克．

(“希望杯”邀请赛试题)

5．某农民在农贸市场卖鸡,甲先买了总数的一半又半只,然后乙买了剩下的一半又半只,最后丙买了剩下的一半又半只,恰好买完．则该农民一共卖了_________只鸡．

(“希望杯”邀请赛试题)

6．如图算式中,每个汉字代表1个数字,不同的汉字代表不同的数字,已知“神”＝3,那么被乘数是_________．

(第6题)

(“五羊杯”竞赛题)

7．在某校辅导计划中,若干名一年级学生可与一名六年级学生成为好友,而一名六年级学生不能与多名一年级学生成为好友．已知的六年级学生与的一年级学生成为好友．则在一年级与六年级学生中好友人数占这两个年级人数的(　)．

(美国数学竞赛题)

8．某晚,学生克洛伊、佐伊先各自独立解决了家庭作业中一半的问题,然后再一起合作解决了另一半问题．克洛伊独自解决问题的正确率为80%,总的解题正确率为88%．已知佐伊独自解决问题的正确率为90%．则佐伊总的解题正确率为(　)．

A．89%　B．92%　C．93%　D．96%　E．98%

(美国数学竞赛题)

9．某服装厂生产某种类型冬装,9月份销售冬装的利润(每件冬装的利润＝出厂价－成本)是出厂价的25%,10月份将每件冬装的出厂价调低10%(每件冬装的成本不变),销售件数比9月份增加80%,那么该厂10月份销售这种冬装的利润总额比9月份的利润总额增长(　)．

A．2%　B．8%　C．40．5%　D．62%

(广西壮族自治区竞赛题)

10．一艘轮船从A港到B港顺水航行需6小时,从B港到A港逆水航行需8小时．若在静水条件下,从A港到B港需(　)小时．

(江苏省镇江市中考题)

11．如图,有一种足球是由数块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等．若黑皮有12块,则白皮的块数是(　)．

A．22　B．20

C．18　D．16

(第11题)

(山西省太原市竞赛题)

12．一个水库在年降水量不变的情况下,能够维持全市12万人20年的用水量．在该市新迁入3万人之后,该水库只够维持15年的用水量,市政府号召节约用水,希望能将水库的使用寿命提高到30年．那么,该市市民平均需要节约多少比例的水才能实现政府制订的目标?(　)．

(国家公务员考试行政职业能力测试题)

13．若干个工人装卸一批货物,每个工人的装卸速度相同．若这些工人同时工作,则需要10小时装卸完毕．现改变装卸方式,开始一个人干,以后每隔t(整数)小时增加一个人干,每个参加装卸的人都一直干到装卸结束,且最后增加的一个人的装卸时间是第一个人装卸时间的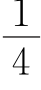．问:

(1)按改变后的装卸方式,自始至终需要多长时间?

(2)参加装卸的有多少人?

(江苏省竞赛题)

14．A,B,C三个微型机器人围绕一个圆形轨道高速运动,它们顺时针同时同地出发后,A在第2秒钟时追上B,第2．5秒钟时追上C,当C追上B时,C和B的运动路程的比是3∶2．问第1分钟时,A围绕这个圆形轨道运动了多少圈?

(“华罗庚金杯”少年数学邀请赛试题)

15．保罗和詹妮每人都有整数值的英镑．保罗对詹妮说:“你若给我3英镑,我的钱数将是你的n倍．”詹妮对保罗说:“你若给我n英镑,我的钱数将是你的3倍．”

若以上陈述真实且n是正整数,n的可能值是多少?

(英国数学奥林匹克试题)

16．在三个正整数的连乘积中,将每个乘数均减小3．试问:它们的乘积能否恰增大2016?

(俄罗斯数学竞赛题)

17．实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示．若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升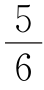cm,问开始注入多少分钟的水量后,甲与乙的水位高度之差是0．5cm?

(第17题)

(浙江省绍兴市中考题)

18．数学与金融

所谓“金融”,即“资金融通”,通俗而言,即“钱的流通”．

股票交易、理财计算、期权定价、住房按揭贷款……

在金融生活中,数学扮演重要角色,而现代金融学的发展与科学大师爱因斯坦、庞加莱、希尔伯特、冯·诺伊曼紧密地联系在一起．

日本著名数学家伊藤清并不是任何意义上的商人,而是地地道道的一流数学家,他的名字出现在商业版的原因是他的工作极大地影响人们对一切随机现象的理解．这其中也包括了金融现象．1997年,伊藤清获得诺贝尔经济学奖,曾被称为“华尔街最有名的数学家”．

(1)书店举行购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元,一律按原价打9折;③一次性购书超过200元,一律按原价打7折．小丽在这次活动中,两次购书总共付款229．4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_________元．

(浙江省绍兴市中考题)

问题17以科学中的连通器为背景,给简单的一元一次方程赋予新的情境,旨在倡导从数学的角度发现问题和提出问题,强化应用意识．

当代美国数学物理学家戴森在《物理科学中的数学》中曾写道:“数学之于物理,不仅是计算现象的工具,更是创造新理论的概念和原理的主要源泉．”

(2)长沙红星大市场某种高端品牌的家用电器,若按标价打8折销售该电器一件,则可获纯利润500元,其利润率为20%．现如果按同一标价打9折销售该电器一件,那么获得的纯利润为(　)．

A．562．5元　B．875元

C．550元　D．750元

(湖南省长沙市中考题)

(3)为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮．其中,甲种粗粮每袋装有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种粗粮每袋装有1千克A粗粮,2千克B粗粮,2千克C粗粮．甲、乙两种袋装粗粮每袋成本价分别为袋中的A,B,C三种粗粮的成本价之和．已知A粗粮每千克成本价为6元,甲种粗粮每袋售价为58．5元,利润率为30%,乙种粗粮的利润率为20%．若这两种袋装粗粮的销售利润率达到24%,求该电商销售甲、乙两种袋装粗粮的数量之比．

(重庆市中考题)

例4　报5的人心里想的数应是8－x,于是,报7的人心里想的数是12－(8－x)＝4＋x,报9的人心里想的数是16－(4＋x)＝12－x,报1的人心里想的数是20－(12－x)＝8＋x,报3的人心里想的数是4－(8＋x)＝－4－x,由x＝－4－x,得x＝－2．

例5　100×0．9＝90＜94．5＜100,300×0．9＝270＜282．8．

设小美第二次购物的原价为x元．则(x－300)×0．8＋300×0．9＝282．8．

解得x＝316．

下面分两种情况讨论:

(1)小美第一次购物没有优惠,第二次购物原价超过300元,则小丽应付

(316＋94．5－300)×0．8＋300×0．9＝358．4(元)．

(2)小美第一次购物原价超过100元,第二次购物原价超过300元,

则第一次购物原价为94．5÷0．9＝105(元)．

所以,小丽应付(316＋105－300)×0．8＋300×0．9＝366．8(元)．

例7　设放牧21头牛n星期吃完,牧场原有草量为a,每星期生长的草量为d,每头牛每星期的吃草量为c,则6(27c－d)＝9(23c－d)＝n(21c－d),解得n＝12．

1．12

2．43　设共有x人,由(x－4－5－7)×6＋2×4＋1×5＝(x－3－4－1)×3＋8×3＋9×4＋10×1,得x＝43．

3．35　设当甲、乙打的字数相同时,乙打了x页,由500×2＋500×＝600x,得x＝35．

4．4．8　5．7

6．307692　设“神舟五号”＝A,“飞天”＝B,则3×(100A＋B)＝10000B＋A,23A＝769B,(23,769)＝1,故B＝23n,A＝769n,n为自然数,2≤n≤4,得n＝4,从而A＝3076,B＝92．

7．B

因为n是自然数,于是,(3y－13)|(y＋9)⇒(3y－13)|(3y＋27)⇒(3y－13)|[(3y＋27)－(3y－13)]⇒(3y－13)|40．

通过枚举可得数据如表,其中“no”表明不可能取值．

经检验,这四组解均合理．

从而,证明了n＝1,2,3,7为仅有的值．

16．可以　用两个1与a相乘,其答案为a,三个数均减小3,后应为(－2)2(a－3)＝4a－12,令4a－12＝a＋2016,得a＝676．

17．本题涉及底面积、注水速度、注水时间,而解题的关键是在理解题意的基础上分类讨论．

可设甲、乙、丙的底面积分别为S、4S、S,向乙、丙注水的时间为t分钟．因为每分钟同时向乙和丙注入相同量的水,所以当注水1分钟可求出丙的水位上升高度:4S×＝S×h丙,解得h丙＝,所以注水1分钟,丙的水位上升为cm．

设开始注入t分钟的水量后,甲与乙的水位高度之差是0．5cm,而甲与乙的水位高度之差是0．5cm时有三种情形:

(1)如图①,当乙的水位低于甲的水位,且乙、丙中的水均未至连通处时,此时＝0．5,解得t＝．

(2)如图②,当甲的水位低于乙的水位,而丙中水至连通处,并溢出到乙中,且甲的水位不变时,此时4S×1．5＋S×5＝,解得

(第17题)