精英数学大视野第8讲解设23个彼此不同的正整数

丢番图,大约生活在公元3世纪,古希腊数学家,代数史上的巨人,左图是他最重要的作品《算术》,该书主要讨论不定代数方程问题．丢番图的另一数学功绩是简化了未知数．《希腊诗文选》中收录了丢番图奇特的墓志铭．

知能概述

字母示数是代数的一个重要特征,是由算术跨越到代数的桥梁,是数学发展史上的一个飞跃．

字母示数具有简明性、一般性,在求代数式的值、形成公式、解应用题等方面有广泛的应用．

为了沟通数量间的关系,或将有些不明朗的关系表示出来,我们需要设元,而所设的字母不能或不需要求出,这就是设而不求的基本含义．

问题解决

例1　一个摩托车手在前旅程中速度是40千米/时,在后旅程中速度是50千米/时,则在他的全程中平均速度为_________．

(江苏省竞赛题)

解题思路　平均速度＝,题设中并未给出总路程,需设出总路程．

楼梯阶数

爱因斯坦曾给他的朋友出了这样一道题:

在你面前有一条长长的阶梯,如果你每步跨2阶,那么最后剩1阶;如果你每步跨3阶,那么最后剩2阶;如果你每步跨5阶,那么最后剩4阶;如果你每步跨6阶,那么最后剩5阶;只有当你能够每步跨7阶时,才正好到头,一阶也不剩．请问:这阶梯至少有多少阶?

以符代数,即以字母代替数．韦达在《分析术引论》(1591年出版)中使用字母来表示未知数以及已知数,实现了历史的突破．从此,从算术到代数,代数学告别了旧时代,插上飞翔的翅膀．

符号比语言、文字更简练、更直观、更具一般性．通过“数学符号”来思考数学,是一件格外有趣并令人充满期待的事．

例2　下列四个数中可以写成100个连续自然数之和的是(　)．

A．1627384950　B．2345678910

C．3579111300　D．4692581470

(江苏省竞赛题)

解题思路　设自然数从a＋1开始,这100个连续自然数的和为(a＋1)＋(a＋2)＋…＋(a＋100)＝100a＋5050,从揭示和的特征入手．

例3　在一次数学竞赛中,组委会决定用NS公司赞助的款购买一批奖品．若以1台NS计算器和3本《数学竞赛讲座》书为一份奖品,则可买100份奖品;若以1台NS计算器和5本《数学竞赛讲座》书为一份奖品,则可买80份奖品．问这笔钱全部用来购买计算器或《数学竞赛讲座》书,可各买多少?

(湖北省黄冈市竞赛题)

解题思路　设每台计算器x元,每本《数学竞赛讲座》书y元,利用赞助款不变寻找x,y的关系．

例4　将若干个自然数按某种规律排列,若前8个数依次是1,3,6,10,15,21,28,36,则第50个数是多少?

(世界数学团体锦标赛试题)

解题思路　设已知的数依次是a1,a2,a3,a4,…,a50,…,这若干个自然数排列的规律是什么?怎样求出a50?

通过设元,把隐含的关系表示出来,这些字母在解题中相消或相约,不需求出这些字母的值却可以得到我们想要的结果,这是“设而不求”方法解决问题的基本思想．

有些问题涉及的量比较多,关系复杂,我们就需要引入不同的字母,便于把数量关系表示出来,在解题中我们不需(或不能)求出所有字母的值,只需求出关键的字母的值．

例5　如图,已知四边形ABCD各边的中点E,F,M,N的连线EM,FN交于O,分四边形ABCD的面积三块为6,8,10,求第四块的面积．

(“希望杯”邀请赛试题)

解题思路　连OA,OB,OC,OD,设S△OAE＝S△OBE＝a,S△OBF＝S△OCF＝b,S△OCM＝S△OMD＝c,S△ODN＝S△OAN＝d,将问题转化为求c＋d的值．

例6　从两个重量分别为12千克和8千克,且含铜的百分数不同的合金上切下重量相等的两块,把所切下的每块和另一块剩余的合金放在一起,熔炼后两个合金含铜的百分数相等．求所切下的合金的重量是多少千克?

分析　由于已知条件中涉及合金中含铜的百分数,因此只有增设这两个合金含铜的百分数为参数或与合金含铜的百分数有关的其他量为参数,才能充分利用已知,为列方程创造条件．

解法1　设所切下的合金的重量为x千克,重12千克的合金的含铜百分数为p,重8千克的合金的含铜百分数为q(p≠q),于是有

整理得5(q－p)x＝24(q－p)．

因为p≠q,所以q－p≠0,因此x＝4．8,即所切下的合金重4．8千克．

解法2　设从重12千克的合金上切下的x千克中含铜m千克,从重8千克的合金上切下的x千克中含铜n千克(m≠n),则这两个合金含铜的百分数分别为和．于是有

整理得5x(n－m)＝24(n－m)．

因为m≠n,所以n－m≠0,因此x＝4．8,即所切下的合金重4．8千克．

有些应用题中隐含一些未知的常量,这些量对于求解无直接联系,但如果不指明这些量的存在,则难求其解．因此需把这些未知的常量设为参数,以便建立等量关系,称此为辅助设元．

例7　23个不同的正整数的和为4845,问这23个数的最大公约数可能达到的最大值是多少?写出你的结论,并说明理由．

(“希望杯”邀请赛试题)

解　设这23个彼此不同的正整数为a1,a2,a3,…,a22,a23,且(a1,a2,…,a22,a23)＝d,故可记a1＝db1,a2＝db2,…,a22＝db22,a23＝db23,其中b1,b2,…,b22,b23是互不相等的正整数,由题意得

4845＝d(b1＋b2＋…＋b22＋b23)

∵b1＋b2＋…＋b22＋b23≥1＋2＋…＋22＋23＝276,

∴4845＝d(b1＋b2＋…＋b22＋b23)≥276·d,

即,而4845＝19×17×5×3,

故d最大可能取17．

事实上,若d＝17,则b1＋b2＋…＋b22＋b23＝19×15＝285,试取b1＝1,b2＝2,…,b22＝22,则b1＋b2＋…＋b22＝253,此时取b23＝285－253＝32,正好满足条件．

三阶幻方

相传大禹在治洛水的时候,洛水神龟献给大禹一本洛书,书中有如图所示的一幅奇怪的图,这幅图用今天的数学符号翻译出来,就是一个三阶幻方,也就是在3×3的方阵中填入1～9,其中每行、每列和两条对角线上数字和都相等．

现在人们已给出一般三阶幻方的定义:在3×3的方阵图中,每行、每列、每条对角线上3个数的和都相等,就称它为三阶幻方．

解幻方问题,常需恰当引元,运用幻方定义、性质、整体核算等方法求解．

例8　如图,3×3数表各行、各列及两条对角线之和彼此相等,设为S．求证:

(1)S＝3e;

(2)2(a＋c＋g＋i)＝b＋d＋f＋h＋4e．

(环球城市数学奥林匹克试题)

解题思路　三阶幻方如何构造?熟悉例8揭示的规律及以下性质,是构造的关键．

(1)在三阶幻方中,每个数都加上或都乘以一个相同的数,仍是一个三阶幻方．

(2)d＋f＝b＋h＝a＋i＝c＋g＝2e．

当代著名数学家B．狄隆涅曾说:重大的科学发现,同解答一道好的奥林匹克试题的区别,仅仅在于解一道奥林匹克试题需要花5小时,而取得一项重大科研成果需要花费5000小时．

数学家哈尔莫斯、巴尔布尤把图中每行(列)数字组成一个三位数,并写出它们的逆序数,就得到下列美妙的等式:

492＋357＋816＝618＋753＋294

4922＋3572＋8162＝6182＋7532＋2942

438＋951＋276＝672＋159＋834

4382＋9512＋2762＝6722＋1592＋8342．

1．如图是一组有规律的图案,它们是由边长相同的小正方形组成的,其中部分小正方形涂有阴影,依此规律,第n个图案中有_________个涂有阴影的小正方形(用含有n的代数式表示)．

(第1题)

(山西省中考题)

2．已知17个连续整数的和是306,那么紧接在这17个数后面的那17个整数的和是________．

(天津市竞赛题)

3．如图是一个3×3个的幻方,当空格填上适当的数后,每行、每列以及对角线上的和都是相等的,则k＝_________．

(第3题)

(数学精英邀请赛试题)

4．一条公交线路从起点到终点有8个站,一辆公交车从起点站出发,前6站上车100人,前7站下车80人,则从前6站上车而在终点站下车的乘客有________人．

(“希望杯”邀请赛试题)

5．巴勃罗、索菲亚和米娅在一次聚会上各分得一些糖果．巴勃罗的糖果数为索菲亚糖果数的3倍,索菲亚的糖果数为米娅糖果数的2倍．巴勃罗决定将自己的糖果分给索菲亚和米娅一部分,这样三个人的糖果数相等．则巴勃罗分给索菲亚的糖果数占自己原来糖果数的_________．

(美国数学竞赛题)

6．有四位小朋友,其中每三位小朋友的岁数之和分别为22,20,17,25,则这四位小朋友中年龄最大的比年龄最小的大(　)岁．

A．4　B．5　C．6　D．7　E．8

(国际中小学数学能力检测试题)

7．某研究所全体员工的月平均工资为5500元,男员工月平均工资为6500元,女员工月平均工资为5000元,则该研究所男、女员工人数之比是(　)．

A．2∶3　B．3∶2　C．1∶2　D．2∶1

(“希望杯”邀请赛试题)

8．当克拉拉计算自己各科测试成绩的总分时,无意识地将某一科分数的十位与个位交换了位置,则最有可能是错误的总分与正确的总分相差的分数是(　)．

A．45　B．46　C．47　D．48　E．49

(美国数学邀请赛试题)

9．老师报出一个5位数,同学们将它的顺序倒排后得到的5位数减去原数,学生甲、乙、丙、丁的结果分别是34567,34056,23456,34956．老师判定4个结果中只有1个正确,答对的是(　)．

A．甲　B．乙　C．丙　D．丁

(四川省竞赛题)

10．某校初一、初二两个年级学生的人数相同,初三年级的学生人数是初二年级学生人数的,已知初一年级的男生人数与初二年级的女生人数相同,初三年级男生人数占三个年级男生人数的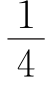,那么三个年级女生人数占三个年级学生人数的比是(　)．

(“希望杯”邀请赛试题)

11．已知有一列数a1,a2,…,an满足关系:后面的这个数依次比它前面的一个数大k(k为定值),且3(a3＋a5)＋2(a7＋a10＋a13)＝24,求a1＋a2＋…＋a13的值．

(浙江南苍南中学自主招生试题)

12．某次数学竞赛前60名获奖,原定一等奖5人,二等奖15人,三等奖40人;现调为一等奖10人,二等奖20人,三等奖30人．调整后一等奖平均分数降低3分,二等奖平均分数降低2分,三等奖平均分数降低1分．如果原来二等奖比三等奖平均分数多7分,求调整后一等奖比二等奖平均分数多几分?

(“华罗庚金杯”少年数学邀请赛试题)

13．山脚下有一池塘,山泉以固定的流量(即单位时间里流入池中的水量相同)不停地向池塘内流淌,现池塘中有一定深度的水,若用一台A型抽水机则1小时后正好能把池塘中的水抽完,若用两台A型抽水机20分钟正好把池塘中水抽完．问:若用三台A型抽水机同时抽,则需要多长时间恰好把池塘中的水抽完?

(江苏省竞赛题)

14．甲和乙同时分别从A,B两地出发以各自的匀速度相向行走(两人的速度可不同),相遇于C点．若甲比乙早出发30分钟,则他们的相遇点到B的距离比C到B的距离少2公里．若乙比甲早出发30分钟,则他们的相遇点到A的距离比C到A的距离少,少多少公里?

(环球城市数学奥林匹克试题)

15．将一个正方形分成如图所示的6个面积相等的长方形,在长方形ABCD中,求AB∶BC的值．

(第15题)

(俄罗斯数学奥林匹克试题)

例2　A　这100个连续自然数的和的最末两位数是50．

例4　1275　由题意得

a2－a1＝2,

a3－a2＝3,

a4－a3＝4,

……

a49－a48＝49

a50－a49＝50,

以上49个式子左、右两边分别相加,得

∴a50＝1274＋1＝1275,即其中的第50个数是1275．

例5　8　由条件得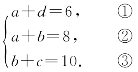

③－②,得

c－a＝2,　④

①＋④,得d＋c＝8．

例8　(1)S＝a＋e＋i＝b＋e＋h＝c＋e＋g＝d＋e＋f,相加得4S＝a＋b＋c＋d＋e＋f＋g＋h＋i＋3e,故S＝3e．

(2)S＝a＋b＋c＝b＋e＋h,故a＋c＝e＋h,同理a＋g＝e＋f,g＋i＝e＋b,c＋i＝e＋d,四式相加得2(a＋c＋g＋i)＝b＋d＋f＋h＋4e．

1．(4n＋1)

2．595　设17个连续整数为m,m＋1,m＋2,…,m＋16,且m＋(m＋1)＋…＋(m＋16)＝306,它后面紧接的17个连续自然数应为m＋17,m＋18,m＋19,…,m＋33,可得它们的和为595．

3．231　如图,由a＋k＋b＝a＋c＋121及c＋d＋11＝b＋d＋121,得k＋b＝c＋121,c＝110＋b,从而k＝110＋121＝231．

(第3题)

4．20　设前7站上车的乘客数量依次为a1,a2,a3,a4,a5,a6,a7人,从第2站到第8站下车的乘客数量依次为b2,b3,b4,b5,b6,b7,b8人,则

a1＋a2＋a3＋a4＋a5＋a6＋a7＝b2＋b3＋b4＋b5＋b6＋b7＋b8,

又a1＋a2＋a3＋a4＋a5＋a6＝100,b2＋b3＋b4＋b5＋b6＋b7＝80．

得100＋a7＝80＋b8,即b8－a7＝100－80＝20．

表明从前6站上车而在终点站下车的乘客共20人．

5．

6．E　设四位小朋友的岁数之总和为x,则四个小朋友的岁数分别为x－22,x－20,x－17,x－25,(x－17)－(x－25)＝8．

7．C

8．A　总分相差的分数一定是9的倍数．

9．B　设原数为,则－m＝11×[909(e－a)＋90(d－b)]是11的倍数．

10．C　设初一年级学生人数为a,男生人数为b,可求得初三年级男生人数为,所求比为:

11．a2＝a1＋k,a3＝a1＋2k,a5＝a1＋4k,a7＝a1＋6k,a10＝a1＋9k,a13＝a1＋12k,代入等式,得a1＋6k＝2．

∴原式＝13a1＋(k＋2k＋…＋12k)＝13(a1＋6k)＝26．

12．设调整后一等奖、二等奖、三等奖平均分数各为x,y,z分,由题意得

于是x－y＝5．

13．设流水的速度为xm3/min,池塘原有水ym3,每台A型抽水机抽水效率为zm3/min,三台A型抽水机需t分钟把池塘中水抽完,由题意得

(第14题)