高斯的计算天赋：不同方法解决数学问题

阿基米德(公元前287—前212),古希腊最伟大的数学家,他与牛顿、高斯并列为三大数学家,并被誉为“数学之神”．阿基米德是在叙拉古陷落时被杀的,相传罗马士兵杀害他时,他正专注于沙盘里的图形．当代著名哲学家、数学家怀特海说:“这是世界发生头等重要变化的一个标志．”

知能概述

计算能力是计算技能与逻辑推理能力的结合．这要求我们在理解有理数相关概念和计算法则的基础上,在掌握法则、公式、算理算律的基础上,能善于观察问题的结构特点,选择合理而又简捷的算法,提高计算的准确性和速度．

有理数常用的方法与技巧有:

巧用运算律、字母代数、错位相减、倒序相加、分解相约、拆项相消、利用公式等．

问题解决

例1　(1)已知a,b互为倒数,c,d互为相反数,e＜0,且|e|＝1,那么(－ab)2003－(c＋d)2004－e2005的值为(　)．

(江苏省竞赛题)

(2)如图,要输出大于100的数,则输入的正整数x最小值是_________．

(“希望杯”邀请赛试题)

解题思路　对于(1),从倒数、相反数的概念入手;对于(2),读懂程序图．

我们有些青少年学习数学时,害怕运算,特别是比较复杂一些的计算题,他们往往半途而废……要学好数学,就要不怕繁,不怕难,要有算到底的决心．

——华罗庚

最大的数

“用三个9拼成一个最大的数”,这是两千多年前,古希腊哲学家柏拉图提出的一个问题．

例2　如果4个不同的正整数m,n,p,q满足(7－m)(7－n)(7－p)(7－q)＝4,那么m＋n＋p＋q等于(　)．

A．10　B．21　C．24　D．26　E．28

(新加坡数学竞赛题)

解题思路　解题的关键是把4表示成4个不同整数积的形式．

例3　计算:

(1)

(“五羊杯”竞赛题)

(2)1＋3＋32＋33＋…＋39＋310;

(《时代学习报》数学文化节试题)

(“创新杯”竞赛题)

解题思路　整体考虑,化繁为简．对于(2),由于相邻的后一项与前一项的比都是3,从用字母表示和式入手;对于(3),注意括号内数式的联系,引入字母,将复杂的数值计算转化为简单的式子再计算．

例4　计算:

(1)

(“希望杯”邀请赛试题)

(2)

(“五羊杯”竞赛题)

解题思路　,…,拆项相消简化计算．

“悟,觉也”,即理解、领会、觉醒之意．表现为由迷惑而明白,由模糊而清晰;表现为一种在紧张的沉思后突然获解所产生的豁然开朗的心理状态,表现为一种打破常规思维的突破．

拆项常用到以下关系式:

例6　在1,2,…,2002前面任意添上正号和负号,求其非负代数和的最小值．

(俄罗斯数学竞赛题)

分析与解　首先确定非负代数和的最小值的下限,然后通过构造法证明这个下限可以达到即可．整数的和差仍是整数,而最小的非负整数是0．代数和的最小值能是0吗?能是1吗?由于任意添“＋”号或“－”号,形式多样,因此,不可能一一尝试再作解答,可从奇数、偶数的性质入手．

因a＋b与a－b的奇偶性相同,故所求代数和的奇偶性与1＋2＋3＋…＋的奇偶性相同,即为奇数．因此,所求非负代数和不会小于1．

又∵(－1＋2)＋(3－4－5＋6)＋(7－8－9＋10)＋(11－12－13＋14)＋…＋(1999－2000－2001＋2002)＝1,

∴所求非负代数和的最小值为1．

裂项相消中的类比

类比是一种推理方法,即根据两种事物在某些特征上的相似,作出它们在其他特征上也可能相似的结论．

触类旁通,即用类比的方法提出问题及寻求解决问题中的途径和方法．

光和声,这两类现象具有许多相同的性质,如它们都是直线传播,都有折射与反射现象等．根据声的波动性质,荷兰著名科学家惠更斯得出“光可能有波动的性质”的猜想．后来,光的波动性质通过实验得到了证实．

开普勒曾说:“我珍视类比胜过任何东西,它是我最可信赖的老师,它能揭示自然界的秘密．”

例5用到字母、示数、错位相减等计算方法．

著名数学教育家波利亚在《怎样解题》一书中曾说:“没有任何一个问题是彻底完成了的,总还会有事情可以做,在经过充分的研究和洞察以后,我们可以对问题有更深刻的理解．”

对于例6,我们可进一步讨论如下问题:

在1,2,…,n前面添上正号和负号,其非负代数和是否都有最小值?如果有,怎样求出最小值?

观察下列的计算过程:

这就是解稍复杂的计算中常用到的裂项相消法,即把每项恰当拆分,使得其中部分数相互抵消,简化计算．

用类比的方法能提出更多的问题吗?

从连续自然数到连续偶数、奇数;从2个到3个或4个;从分数到整数,类比可提出许多计算问题．

形如Sp(n)＝1p＋2p＋3p＋…＋np(p为正整数)的和式称为自然数幂和,也称为p阶自然数幂．探究低阶自然数幂和的公式,历史上的数学家的智慧为我们提供了有益的借鉴．

例7　计算:

(1)1＋2＋3＋…＋n;

(2)1×2＋2×3＋3×4＋…＋n(n＋1);

(3)12＋22＋32＋…＋n2;

(4)13＋23＋33＋…＋n3．

解题思路　问题(1)的解决为其他问题的解决提供帮助,而其解决的常用方法有:拆项相消、倒序相加、数形结合等．拆项相消具有一般性,需要突破分数拆项的思维定式,如n(n＋1)]．

1．(1)计算:

(江苏省南京市中考题)

(2)“数学王子”高斯从小就善于观察和思考,在他读小学时就能在课堂上快速地计算出1＋2＋3＋…＋98＋99＋100＝5050,今天我们可以将高斯的做法归纳如下:

S＝1＋2＋3＋…＋98＋99＋100,　①

数学学习中,类比思想的运用有下列常见情形．

概念的类比,

方法的类比,

结构模型的类比,

与简单问题类比,

低维与高维的类比,

从特殊到一般的类比推介等．

S＝100＋99＋98＋…＋3＋2＋1,　②

①＋②有2S＝(1＋100)×100,S＝5050．

请类比以上做法,回答下列问题:

若n为正整数,3＋5＋7＋…＋(2n＋1)＝168,则n＝_________．

(湖北省黄石市中考题)

2．计算:

(1)2－22－23－24－…－218－219＋220＝________．

(“缙云杯”竞赛题)

(2)＝_________．

(广西壮族自治区竞赛题)

(3)＝________．

(国际少年数学精英大会自主试题)

3．依次排列4个数:2,11,8,9．对相邻的两个数,都用右边的数减去左边的数,所得之差排在这两个数之间得到一串新的数:2,9,11,－3,8,1,9．这称为一次操作．做第二次操作后得到一串新的数:2,7,9,2,11,－14,－3,11,8,－7,1,8,9．这样下去,第100次操作后得到的一串数的和是________．

(“华罗庚金杯”少年数学邀请赛试题)

4．已知,则小于S的最大整数是_________．

(“华罗庚金杯”少年数学邀请赛试题)

5．图中的程序表示,输入一个整数便会按程序进行计算．

(第5题)

设输入的x值为18,那么根据程序,第1次计算的结果是9,第2次计算的结果是4,…,这样下去第5次计算的结果为_________;第2009次计算的结果是________．

(《时代学习报》数学文化节试题)

6．若有理数a,b,c两两不等,则中负数的个数是(　)．

A．3　B．2　C．1　D．0

(“希望杯”邀请赛试题)

7．已知有理数a≠1,我们把称为a的差倒数,如:2的差倒数是＝－1,－1的差倒数是．如果a1＝－2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数…依次类推,那么a1＋a2＋…＋a100的值是(　)．

A．－7．5　B．7．5　C．5．5　D．－5．5

(山东省济宁市中考题)

8．已知整数a,b,c,d满足abcd＝25,且a＞b＞c＞d,那么|a＋b|＋|c＋d|等于(　)．

A．0　B．10　C．2　D．12

(江苏省竞赛题)

9．观察等式:2＋22＝23－2;2＋22＋23＝24－2;2＋22＋23＋24＝25－2;…．已知按一定规律排列的一组数:250,251,252,…,299,2100．若250＝a,用含a的式子表示这组数的和是(　)．

A．2a2－2a　B．2a2－2a－2　C．2a2－a　D．2a2＋a

(武汉市中考题)

10．若有理数x,y使得x＋y,x－y,xy,这四个数中的三个数相等,则|y|－|x|的值是(　)．

(天津市竞赛题)

11．计算:

(北京市“迎春杯”竞赛题)

(“南方杯”数学邀请赛试题)

(“五羊杯”竞赛题)

(北京市竞赛题)

12．乘方之美

乘方之美、乘方之趣、乘方之奇,有多少耐人寻味且神奇的现象隐藏于乘方之中．

(1)观察下列等式:

31＝3,32＝9,33＝27,34＝81,35＝343,36＝729,37＝2187……解答下列问题:3＋32＋33＋34＋…＋32013的末位数字是(　)．

A．0　B．1　C．3　D．7

(江苏省泰安市中考题)

(2)已知n个数x1,x2,…,xn,每个数只能取0,1,－1中的一个．若x1＋x2＋…＋xn＝2019,则x21019＋x22019＋…＋xn201　9的值为________．

(“华罗庚金杯”少年数学邀请赛试题)

(3)假设将一张普通的纸对折50次,估算有多厚?一张纸可以重复对折多少次?

(4)“判天地之美,析万物之理”,这是出自《庄子·天下篇》．在中国古代圣贤中,庄子是最独特的,最富于想象力的．齐视万物,以求逍遥．《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭．”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完．即计算:

13．有人编了一个程序:从1开始,交替地做加法或乘法(第一次可以是加法,也可以是乘法),每次加法,将上次运算结果加2或加3;每次乘法,将上次运算结果乘2或乘3,例如,30可以这样得到:

(1)证明:可以得到22;

(2)证明:可以得到2100＋297－2．

(全国初中数学联赛试题)

14．已知,其中m与n互质,求证:2017|m．

(“希望杯”邀请赛试题)

15．在的小方格中填上“＋”“－”号,如果可以使其代数和为n,就称数n是“可被表出的数”,否则,就称数n是“不可被表出的数”(如1是可被表出的数,这是因为＋1＋2－3－4＋5＋6－7－8＋9是1的一种可被表出的方法)．

(1)求证:7是可被表出的数,而8是不可被表出的数．

(2)求25可被表出的不同方法种数．

(四川省竞赛题)

16．已知有理数a1,a2,…,a2013满足a1＋a2＋…＋a2013＝0,且|a1－2a2|＝|a2－2a3|＝…＝|a2012－2a2013|＝|a2013－2a1|,求证:a1＝a2＝…＝a2013＝0．

(北京大学自主招生试题)

17．一个自然数n若能表示为若干个正整数的和,且这些正整数的倒数和也恰等于1,则称n为“金猴数”,比如:2＋4＋8＋8＝22且＝1,22就是一个“金猴数”．

(1)证明:11与28是两个“金猴数”;

(2)证明:如果n是“金猴数”,则2n＋2,2n＋9也是“金猴数”;

(3)请你判定:2016也是“金猴数”．

(北京市竞赛题)

请看下面曾在网上很火爆的式子:

1．01365＝(1＋0．01)365≈37．8;

0．99365＝(1－0．01)365≈0．03．

进一步,

1．02365＝(1＋0．02)365≈1377;

0．98365＝(1－0．02)365≈0．0006．

365天后,一个增长到了37．8,一个减少到0．03．

早在千年前,我国田园诗人陶渊明曾写下:“勤学如春起之苗,不见其增,日有所长;辍学如磨刀之石,不见其损,日有所亏．”一个与乘方相关的数学式子与一个文学诗句不是有相同的意境吗?

例1　(1)0

(2)22　当x为偶数时,由5x＞100,得x＞20,则正整数x的最小值为22;

当x为奇数时,由4x＋13＞100,得x＞21．75,则正整数x的最小值为23．

故要使输出值大于100,则输入的最小正整数x是22．

例2　E　4＝2×(－2)×1×(－1)．

(2)设S＝1＋3＋32＋33＋…＋39＋310,　①

则3S＝3＋32＋33＋…＋310＋311,　②

1．(1)(2)12　由＝168,得n(n＋2)＝12×14．

2．(1)6　2n＋1－2n＝2n．

(2)885　设原式＝S,将括号反序相加．

故小于S的最大整数是0．

5．－4,－4　输入18,依次得到结果:9,4,2,1,－4,－2,－1,－6,－3,－8,－4,－2,－1…显然,除去前4次的结果外,从第5次的结果－4开始,每6次一循环,而(2009－4)÷6＝334余1,故第2009次计算的结果是－4．

6．B

8．D

9．C　2＋22＋23＋…＋2100＝2101－2,2＋22＋23＋…＋249＝250－2,两式相减得250＋251＋252＋…＋2100＝2101－250＝2×250×250－250＝2a2－a．

11．(1)－21

12．(1)C

(2)2019　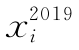＝xi(i＝1,2,…,n),原式＝x1＋x2＋…＋xn＝2019．

(3)通过测量可知一张普通的纸厚度约为0．1mm．

将一张普通的报纸对折50次,其厚度为250×0．1≈1．1259×1014mm,

其厚度将达到11259万千米,相当于地球到太阳的距离．

对折一张纸也许很多人觉得容易,下表直观解释提升纸重复对折的次数是如此困难．

由表可见,纸厚度随着对折次数以等比序列增加,而其面积相应地以同样的比例减少,加上纸本身的拉力,将纸对折第9次无疑比一次将512张报纸对折要更困难．

(4)分步计算,得出规律;或错位相减;而以形助数,则形象直观．

即运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来．

∵2017为质数,且2017与1×2×…×2016互质,

∴2017|m．

15．(1)因为＋1－2－3＋4＋5－6＋7－8＋9＝7,所以,7是可被表出的数．

又＋1＋2＋3＋4＋5＋6＋7＋8＋9＝45是奇数,而对于任意两个整数a,b,有a＋b与a－b具有相同的奇偶性,因此,无论怎样填“＋”“－”号,所得代数和一定是奇数,不可能为8．所以,8是不可被表出的数．

(2)设填“＋”号的数字和为x,填“－”号的数字和为y,则x－y＝25．

又x＋y＝1＋2＋…＋9＝45,则x＝35,y＝10．

因为9＜10,1＋2＋3＋4＝10,所以,填“－”号的那些数字至少有2个,至多有4个．

由此可知,填“－”号的数之和为10．

接下来只要在和为10的那些数前面填“－”号,其余的数前面填“＋”号,就得到25的一种表示方法．所以,只要计算出从1到9中选出若干个其和为10的数字的不同方法,就得到25可表示的不同方法种数．

(ⅰ)10等于两数之和:10＝1＋9＝2＋8＝3＋7＝4＋6,共有4种方法;

(ⅱ)10等于三数之和:10＝1＋2＋7＝1＋3＋6＝1＋4＋5＝2＋3＋5,共有4种方法;

(ⅲ)10等于四数之和:10＝1＋2＋3＋4,只有1种方法．

综上,25可被表出的不同方法共有4＋4＋1＝9种．

16．根据条件知:(a1－2a2)＋(a2－2a3)＋(a3－2a4)＋…＋(a2013－2a1)＝－(a1＋a2＋a3＋…＋a2013)＝0．　①

另一方面,令|a1－2a2|＝|a2－2a3|＝|a3－2a4|＝…＝|a2013－2a1|＝m,

则a1－2a2,a2－2a3,a3－2a4,…,a2013－2a1中每个数或为m或为－m．

设其中有k个m,(2013－k)个－m,则

(a1－2a2)＋(a2－2a3)＋(a3－2a4)＋…＋(a2013－2a1)＝k×m＋(2013－k)×(－m)＝(2k－2013)m．　②

由①②知:(2k－2013)m＝0．

而2k－2013为奇数,不可能为0,所以m＝0．于是知:

a1＝2a2,a2＝2a3,a3＝2a4,…,a2012＝2a2013,a2013＝2a1．

从而知:a1＝22013·a1,即得a1＝0．同理可知:a2＝a3＝…＝a2013＝0．命题得证．

17．(1)略

所以2n＋9也是个“金猴数”．

(3)由于在(1)中已证28是“金猴数”,再根据(2),于是有

28×2＋2＝58是“金猴数”,

58×2＋2＝118是“金猴数”,

118×2＋9＝245是“金猴数”,

245×2＋9＝499是“金猴数”,

499×2＋9＝1007是“金猴数”,

所以,1007×2＋2＝2016是“金猴数”．