毕达哥拉斯学派及其贡献——毕达哥拉斯定理与带余除法

这是毕达哥拉斯纪念碑,碑体呈直角三角形形状．毕达哥拉斯是古希腊哲学家、数学家,创建了宗教、政治、学术合一的著名的毕达哥拉斯学派,该学派信奉“万物皆数”,发现了毕达哥拉斯定理,定义了奇数、偶数、完全数、亲和数等概念,研究了图形数的规律．

知能概述

用一个正整数b去除另一个正整数a,若商为q,余数为r,则有a＝bq＋r(0＜r＜b)．余数有以下基本性质:

(1)b|(a－r);

(2)一个正整数a被另一个正整数n(n＞1)除时,余数只可能是0,1,2,…,(n－1)中的一个,这样我们可以把整数按余数来分类;

(3)若两个正整数a,b被m除所得的余数相同,则称a与b对模m同余,记作a≡b(modm),即(a－b)被m整除．

解与余数相关问题的基本方法是:恰当运用相关性质,灵活进行代数恒等变形,适时兼顾分类讨论．

问题解决

例1　一个自然数N被10除余9,被9除余8,被8除余7,被7除余6,被6除余5,被5除余4,被4除余3,被3除余2,被2除余1,则N的最小值是_________．

(北京市竞赛题)

解题思路　化不整除问题为整除问题,即N＋1能分别被2,3,4,5,6,7,8,9,10整除．

许多艺术能够美化人的心灵,但却没有哪一种艺术能够比数学更有效地去美化和修饰人们的心灵．

——毕林斯利

物不知数

“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何．”

这是记载于《孙子算经》中的一个问题,《孙子算经》约成书于公元4至5世纪,因载“物不知数”题而名声大震．

从完整的计算程序和理论上解决这个问题的,是南宋时期的数学家秦九韶．秦九韶在他的《数书九章》中提出了一个数学方法“大衍求一术”,系统地论述了一次同余式组解法的基本原理和一般程序．

例2　今天是星期日,那么,今天以后的第20053天是(　)．

A．星期三　B．星期四　C．星期五　D．星期六

(山西省太原市竞赛题)

解题思路　只需考察20053被7除的余数,注意到2005＝7×286＋3．

例3　已知1059,1417,2312分别被自然数x除时,所得的余数都是y,求x－y的值．

(天津市竞赛题)

解题思路　由被除数、除数、余数的关系,建立关于x,y的方程组．

例4　证明:对任意的整数n,n(n＋1)(2n＋1)的值总是整数．

(四川省竞赛题)

解题思路　对任意的整数n,2|n(n＋1),只要证明3|n(n＋1)(2n＋1),将全体整数都除以3,按余数分为{0},{1}和{2}三类,需证明整数n取每一类中的任何一个数,3|n(n＋1)(2n＋1)．

例5　求证:任意三个连续自然数的两两之积的和不可能等于30000．

(全俄中学生数学竞赛题)

解题思路　设三个连续的自然数为n－1,n,n＋1,正难则反,建立n的方程;或从余数考虑．

化不整除为整除、穷举、布列方程组等,是解决带余除法相关问题的常用技巧．

同余是由大数学家高斯引入的一个概念,即“余同”具有“余数相同”这一性质,这种为比较两个整数性质,引入一个参照物的思想是同余理论的一个出发点．

同余是初等数论的一门语言,它为许多数论问题的叙述赋予了统一的、本质的形式．

例6　任给五个整数,证明:必能从中取出三个,使得它们的和能被3整除．

(加拿大数学奥林匹克试题)

证明　一个整数被3除的余数,只有0,1,2三种．如果这五个数中,被3除的余数0,1,2都出现了,那么,余数为0,1,2的三数之和一定能被3整除;

如果这五个数中,被3除的余数0,1,2都没有同时出现,其中必有一个余数至少出现3次,那么,余数相同的三个数的和一定能被3整除．

例7　已知定理:“若三个大于3的质数a,b,c满足关系2a＋5b＝c,则a＋b＋c是整数n的倍数．”试问:上述定理中的整数n的最大可能值是多少?并证明你的结论．

(全国初中数学联赛题)

解n的最大值是9,证明如下:

先证a＋b＋c是3的倍数．

因为a＋b＋c＝a＋b＋2a＋5b＝3a＋6b＝3(a＋2b),所以,a＋b＋c是3的倍数．

再证a＋b＋c是9的倍数．

设a,b被3除的余数分别是ra,rb(ra,rb为0,1,2),

因为a,b是大于3的质数,所以ra≠0,rb≠0,ra,rb只能为1,2．

若ra≠rb,则ra＝1,rb＝2或ra＝2,rb＝1,

此时c＝2a＋5b必为3的倍数,与c为质数相矛盾,故ra＝rb．

所以ra＝rb＝1或ra＝rb＝2,此时,a＋2b必是3的倍数,

因此,a＋b＋c＝3(a＋2b)必是9的倍数．

最后证9是最大的．

当ra＝rb＝1时,取a＝13,b＝7,则c＝2×13＋5×7＝61,

所以a＋b＋c＝13＋7＋61＝81．

当ra＝rb＝2时,取a＝11,b＝5,则c＝2×11＋5×5＝47,

所以a＋b＋c＝11＋5＋47＝63．

而81,63的最大公约数是9,所以n的最大值是9．

反证法

当直接求解问题困难时,不妨从问题的反面(对立面)间接求解,即先假设问题中的结论的反面事项成立,由此出发,运用问题中的条件,通过逻辑推理,设法导出矛盾的结果,从而判断原问题的反面事项不成立,并推出原问题中的结论一定正确．

例8　n位正整数A的所有数字都不为0,从A中任意去掉m个数字后得到的(n－m)位数都不是9的倍数(1≤m≤n－1),求A的最大值．

(“希望杯”邀请赛试题)

分析与解　若直接确定n的范围困难,不妨从反面考虑．

首先,A的所有数字中都不能有9,否则去掉其他数字得到的数是9的倍数．

例6是1970年加拿大数学奥林匹克试题,70年代末,我国著名数学家柯召猜想,它的一般情况是:任给2n－1个整数,必能从中取出n个,使得它们的和能被n整除,单墫教授证明了这个猜想．

数学奥林匹克是智力的角逐,意志力的较量．

20世纪著名数学家波利亚曾说:“如果他(指老师)把分配给他的时间都用来让学生操练一些常规运算,那么他就会扼杀他们的兴趣,阻碍他们的智力发展,从而错失他的良机．相反的,如果他用和学生的知识相称的题目来激发他们的好奇心,并用一些鼓励性的问题去帮助他们解答问题,那么他就能培养学生独立思考的兴趣,并教给他们某些方法．”

下面用反证法证明:n≤9．

假设n≥10,则根据抽屉原理可知,在

a1,a1＋a2,a1＋a2＋a3,…,a1＋a2＋a3＋…＋an

这n个数中必有两个数除以9,得到的余数相同．

设a1＋a2＋a3＋…＋ai与a1＋a2＋a3＋…＋aj被9除的余数相同(其中i＜j),两式相减得ai＋1＋ai＋2＋…＋aj是9的倍数．

此时,去掉其他数字得到的是 9的倍数,与题设条件矛盾．

所以A至多是9位数．

综上,A的最大值为888888888．

1．一个三位自然数,当它分别被2,3,4,5,7除时,余数都是1,那么具有这个性质的最小三位数是________;最大三位数是_________．

(“希望杯”邀请赛试题)

2．中国剩余定理

此定理源于我国古代数学名著《孙子算经》,其中记载了这样一个“物不知数”问题:“今有物不知数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”这个问题的意思是:有一个正整数,除以3余2,除以5余3,除以7余2,求符合条件的正整数．此问题及其解题原理在世界上颇负盛名,中外数学家们称之为“孙子定理”“中国剩余定理”或“大衍求一术”等．对以上“物不知数”问题,求得满足条件的最小正整数为_________,而满足条件的所有正整数可用代数式表示为________．

(《时代学习报》数学文化节试题)

3．今天是星期日,从今天算起,第天是星期_________．

(江苏省竞赛题)

4．用自然数n去除63,91,130,所得到的3个余数的和为26,则n＝________．

(北京市“迎春杯”竞赛题)

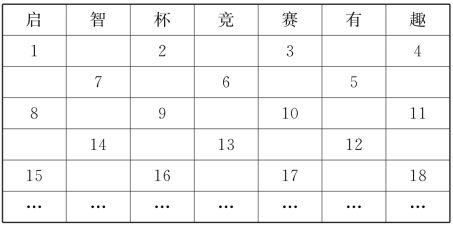
5．自然数1,2,3,…,按下表规律排列:横排为行,记数据1,2,3,4的那一行为第一行,依次记下面的各行分别是第2行,第3行…．试问2011位于该表的第_________行,并对应于“启智杯竞赛有趣”中的汉字:________．

法国著名数学家阿达玛关于反证法有一个精辟的论述:“这种证法在于表明,如果肯定定理的假设,而否定其结论,就一定会导致矛盾．”

费恩曼是20世纪美国杰出的物理学家,他的自传体小说《费恩曼先生,你肯定是在开玩笑》是一本受人称道的传世佳作．书中指出一个充满“禅机”的数＝0．00411522633744855……数字排列井然有序,曾有人怀疑是一个密码,继续下去,有怎样的结果?

(深圳市“启智杯”数学思维能力竞赛题)

6．(1)循环小数的小数点后第2010个数字是_________;若将此数保留2010个有效数字,则所得新数的各位数字中1的个数是_________．

(2)已知＝0．a1a2a3…an…,(其中a1,a2,a3,…都是介于0和9之间的整数),若小数点后连续n个数字之和a1＋a2＋a3＋…＋an＝2013,则an＝________,n＝________．

(世界数学团体锦标赛试题)

7．斐波那契数列

斐波那契(约1170—1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列),后来人们在研究它的过程中,发现了许多意想不到的结果．在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用．

有一列数1,1,2,3,5,8,13,21,…从第三个数起,每一个数都等于它前面两个数的和,这就是著名的斐波那契数列,则这列数中的第2014个数被7除的余数为_________．

(北京市竞赛题)

8．除以8和9都余1的所有三位数的和是(　)．

A．6492　B．6565　C．7501　D．7514

(“五羊杯”竞赛题)

9．已知a＝,则a除以84所得余数是(　)．

A．0　B．21　C．42　D．63

(北京市竞赛题)

10．已知m是被3除余1,被7除余5,被11除余4的最小自然数,则m被4除的余数是(　)．

A．0　B．1　C．2　D．3

(“五羊杯”竞赛题)

11．如图,字母A到G分别代表1到7中的一个自然数,若A＋G＋D,B＋G＋E,C＋G＋F分别被3除,都余1,则G是(　)．

A．1或4　B．1或7

C．4或7　D．1,4或7

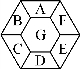
(第11题)

(“希望杯”邀请赛试题)

12．盒中原有7个球,一位魔术师从中任取几个小球,把每一个小球都变成7个小球,将其放回盒中;他又从盒中任取一些小球,把每一个小球都变成7个小球后放回盒中．如此进行,到某一时刻,魔术师停止取球变魔术时,盒中球的总数可能是(　)．

A．1990个　B．1991个　C．1992个　D．1993个

(“祖冲之杯”邀请赛试题)

13．1898年6月9日英国强迫清政府签约,将香港土地租借给英国99年．1997年7月1日香港回归祖国,中国人民终于洗刷了百年耻辱．已知1997年7月1日是星期二,那么,1898年6月9日是星期(　)(注:公历纪年,凡年份为4的倍数但不是100的倍数的那年为闰年,年份为400的倍数的那年也为闰年,闰年的二月有29天,平年的二月有28天)．

A．二　B．三　C．四　D．五

(陕西省竞赛题)

14．数119很奇特:当被2除时,余数为1;当被3除时,余数为2;当被4除时,余数为3;当被5除时,余数为4;当被6除时,余数为5．试问:具有这种性质的三位数还有多少个?(　)．

A．0　B．1　C．3　D．7　E．14

(美国数学竞赛题)

15．已知三位数M被3除余1,被5除余2,被7除余3,求M的最大值、最小值．

(“希望杯”邀请赛试题)

16．在1,2,…,2015这2015个正整数中选出k个数,使得其中任意两个不同的数之和均不为50的倍数,求k的最大值．

(上海市竞赛题)

17．设m＝12＋22＋32＋…＋20032,今天是星期一,若算第一天,则第m天是星期几?

(江苏省竞赛题)

18．有三堆石子的个数分别是19,8,9,现在进行如下的操作:每次从这三堆石子中的任意两堆中各取出1个石子,然后把这2个石子都加到另一堆中去,试问:能否经过若干次这样的操作后使得:

(1)三堆石子的数分别是2,12,22;

(2)三堆都是12．

如能,请用最快的操作完成;不能,则说明理由[注:若从第一、二堆各取1个到第三堆,可表示为(19,8,9)⇒(18,7,11)等]．

(五城市联赛题)

19．a1,a2,…,a11是不小于2的互异正整数,满足a1＋a2＋…＋a11＝407．问:是否存在正整数n,使得当n分别除以a1,a2,…,a11,4a1,4a2,…,4a11这22个数时所得到的余数的和等于2012?

(俄罗斯数学奥林匹克试题)

例1　N＋1为2～10的公倍数,要使N最小,取N＋1为它们的最小公倍数．23×5×32×7＝2520,故所求N的最小值为2520－1＝2519．

例2　D　因20053＝(7×286＋3)3＝7k＋27＝7k1＋6(k,k1都为正整数),故那天是星期六．

例3　设已知三数被自然数x除时,商数分别为a,b,c,

由此得x为358,895,1253的公约数,x＝179,进而求得y＝164．

例4　对任意的整数n,n(n＋1)是偶数,故2|n(n＋1)(2n＋1)．

若n＝3k,则3|n(n＋1)(2n＋1);

若n＝3k＋1,n(n＋1)(2n＋1)＝(3k＋1)(3k＋2)(6k＋3)＝3(3k＋1)(3k＋2)(2k＋1),

则3|n(n＋1)(2n＋1)．

若n＝3k＋2,n(n＋1)(2n＋1)＝(3k＋2)(3k＋3)(6k＋5)＝3(3k＋2)(k＋1)(6k＋5),

则3|n(n＋1)(2n＋1)．

综上所述,对任意的整数n,3|n(n＋1)(2n＋1),

又(2,3)＝1,故6|n(n＋1)(2n＋1),所以,对任意的整数n,n(n＋1)(2n＋1)的值总是整数．

例5　n(n－1)＋n(n＋1)＋(n－1)(n＋1)＝3n2－1＝3(n2－1)＋2．

它被3除余2,而30000能被3整除．故任意三个连续自然数的两两之积的和不可能等于30000．

1．421,841

2．23,23＋3×5×7k＝105k＋23　我们注意到,该数被3,7除后都余2,而3,7互质,因此,这个数应是21m＋2型的数,23最小,而23被5除余3．所以,满足条件的最小正整数为23,满足条件的所有正整数可用代数式表示为23＋3×5×7k＝105k＋23．

3．三　因111111＝15873×7,2000＝333×6＋2,故被7除的余数与11被7除的余数相同,又11＝7×1＋4．

4．43　设自然数n除63,91,130时,商分别为x,y,z,余数分别为a,b,c,则63＝nx＋a　①,91＝ny＋

17．令S1＝12＋22＋32＋42＋52＋62＋72＝140＝20×7,∴S1是7的倍数,S2＝22＋32＋42＋52＋62＋72＋82＝S1＋82－12＝S1＋9×7,∴S2也是7的倍数,如此递推Sn＋1＝7N＋Sn(n为自然数),得任何连续7个自然数之平方和都是7的倍数,2003＝286×7＋1,m＝12＋(22＋32＋…＋20032),m被7除余1,第m天为星期一．

18．(1)经过6次操作可达到要求:(19,8,9)⇒(21,7,8)⇒(23,6,7)⇒(25,5,6)⇒(24,4,8)⇒(23,3,10)⇒(22,2,12);

(2)不可能．因为每次操作后,每堆石子数要么加2,要么少1,而19,8,9被3除余数分别为1,2,0,经过任何一次操作后余数分别是0,1,2,不可能同时被3整除．

19．不存在．

假设存在那样的n,注意到,一个正整数除以m时余数的最大可能值是m－1．故除以a1,a2,…,a11时所得余数的和不超过407－11＝396,除以4a1,4a2,…,4a11时所得余数和不超过4×407－11＝1617．

如果所有的余数都取最大可能值,则余数的和应为396＋1617＝2013．

由条件知这个和等于2012．故除了一个以外所有余数取最大可能值,另一个取最大可能值减1．这表明,存在一个k使得n除以ak,4ak时,一个余数取最大值,一个取最大值减1．由此推出n＋1,n＋2中一个是ak的倍数,另一个是4ak的倍数．

故ak|(n＋1,n＋2)＝1,这与条件ak≥2矛盾．