数的整除性：找到能被10整除的数的最小组合

泰勒斯是古希腊著名的科学家、哲学家,他在数学上最著名的成就是测量金字塔的高度,以及发现了五个几何命题:对顶角相等、直径将圆平分、等腰三角形底角相等、两角夹一边分别对应的三角形全等、半圆上的圆周角是直角．

知能概述

对于整数a和不为零的整数b,总存在整数m,n使得a＝bm＋n(0≤n＜b),其中m称为商,n称为余数,特别地,当n＝0时,即a＝bm,便称a被b整除(也称a是b的倍数或b是a的约数),记为b|a．

整除有以下基本性质:

1．若a|b,a|c,则a|(b±c);

2．若a|b,b|c,则a|c;

3．若a|bc,且(a,c)＝1,则a|b,特别地,若质数p|bc,则必有p|b或p|c;

4．若b|a,c|a,且(b,c)＝1,则bc|a．

解整除有关问题常用到数的整除性常见特征:

1．被2整除的数:个位数字是偶数;

2．被5整除的数:个位数字是0或5;

3．被4整除的数:末两位组成的数被4整除;被25整除的数,末两位组成的数被25整除;

4．被8整除的数:末三位组成的数被8整除;被125整除的数,末三位组成的数被125整除;

5．被3整除的数:数字和被3整除;

6．被9整除的数:数字和被9整除;

7．被11整除的数:奇数位数字和与偶数位数字和的差被11整除．

问题解决

例1　将四个数字1,2,3,4排成一个四位数,使得这个数是11的倍数,则这样得到的四位数共有_________个．

(江西省竞赛题)

数学不应被想象为一种费解、难懂而又违背常识的东西．实际上,数学正是常识的精微化．

——汤姆逊

亲和数

毕达哥拉斯学派的人常说:“谁是我的朋友,这就像220和284一样．”

220除去本身以外还有11个因数,它们是1,2,4,5,10,11,20,22,44,55,110,这11个因数之和恰好等于284．同理,284的因数1,2,4,71,142之和恰好等于220．

古希腊人把具有这样性质的两个数叫“亲和数”,220和284是第一对“亲和数”．

解题思路　依据被11整除数的特征,先确定相关数的位置．

例2　已知a,b是正整数(a＞b),对于如下两个结论:①在a＋b,ab,a－b这三个数中必有2的倍数;②在a＋b,ab,a－b这三个数中必有3的倍数,其中(　)．

A．只有①正确　B．只有②正确

C．①、②都正确　D．①、②都不正确

(江苏省竞赛题)

解题思路　举例验证,或按剩余类讨论严格证明．

例3　已知7位数是72的倍数,求出所有符合条件的7位数．

(江苏省竞赛题)

解题思路　因72＝8×9,(8,9)＝1,故原数能被8,9整除,运用整数能被8,9整除的性质求出x,y的值．

例4　一个正整数N的各位数字不全相等,如果将N的各位数字重新排列,必可得到一个最大数和一个最小数,若最大数与最小数的差正好等于原来的数N,则称N为“拷贝数”,试求所有的三位“拷贝数”．

(湖北省武汉市竞赛题)

解题思路　设N为所求的三位“拷贝数”,它的各位数字分别为a,b,c(a,b,c不全相等),将其数字重新排列后,连同原数共得到6个三位数: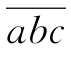,,设其中最大数为,则最小数为,从整除性揭示“拷贝数”的特征．

根据已知条件来确定自然数,是数学活动中常见的一类问题,解这类问题时往往用到下列知识方法:

(1)运用整除性质;

(2)确定首位数字;

(3)利用末位数字;

(4)代数化;

(5)不等式估算;

(6)分类讨论求解等．

例5　证明:对于同样的整数x和y,2x＋3y和9x＋5y能同时被17整除．

(匈牙利数学奥林匹克试题)

解题思路　3(9x＋5y)－5(2x＋3y)＝17x,这是证明本例的关键．

例6　请你将1,2,3,4,5,6,7,8,9这9个数排出一个能被11整除,且最大的九位数,并简述排数的过程．

(重庆市竞赛题)

解法1　设要求的数为N,因为N是11的倍数,所以它的奇数数位的数字之和与偶数数位的数字之和的差是11的倍数,有0,11,22,33,44这五种情况．

因为奇数数位的数字之和与偶数数位的数字之和的和就是1＋2＋3＋4＋5＋6＋7＋8＋9＝45,是一个奇数,我们知道两整数的和与差有相同的奇偶性,所以这个差就只能为11或33．

若这个差为33,因为和为45,故奇数数位的数字之和与偶数数位的数字之和一个为6,一个为39,但1至9这9个数中最小的4个之和为10,大于6,故差不能等于33．即差为11．

由和为45,差为11可以算出奇数数位的数字之和与偶数数位的数字之和一个为17,一个为28．

为使这个九位数最大,我们先将高位安排得尽可能大,先将前四位排成9876,由于偶数数位的数字之和为17,现已有8＋6＝14,偶数数位其他2个数字之和为3,它们只能是2和1．

于是这个九位数为987652413．

解法2　将最大的九位数987654321除以11余数为5,故987654321－5＝987654316是11的倍数．

我们将987654316每次减去11,直到得到一个各位数字均不相同的九位数为止．这样减去173个11后第一次得到一个各位数字均不相同的九位数987652413,这就是满足题目条件的最大的九位数．

局部调整法

对于问题涉及的多个可变对象,使其中部分对象暂时保持不变,只对其中几个对象进行调整,从而化难为易,使问题的解决在局部获得进展．经过若干次这样局部上的调整,不断缩小范围,最终导致整个问题的彻底解决,例6的两种解法就是运用了局部调整法．

例7　从1,2,…,9中任取n个数,其中一定可以找到若干个数(至少有一个,也可以是全部),它们的和能被10整除,求n的最小值．

(《数学周报》杯全国初中数学竞赛题)

分析与解　当n＝4时,数1,3,5,8中没有若干个数的和能被10整除．

当n＝5时,设a1,a2,…,a5是1,2,…,9中的五个不同的数．若其中任意若干个数,它们的和都不能被10整除,则a1,a2,…,a5中不可能同时出现1和9、2和8、3和7、4和6．于是,a1,a2,…,a5中必定有一个数是5．

若a1,a2,…,a5中含1,则不含9．于是,不含4(4＋1＋5＝10),故含6;于是,不含3(3＋6＋1＝10),故含7;于是,不含2(2＋1＋7＝10),故含8．但是5＋7＋8＝20是10的倍数,矛盾．

若a1,a2,…,a5中含9,则不含1．于是,不含6(6＋9＋5＝20),故含4;于是,不含7(7＋4＋9＝20),故含3;于是,不含8(8＋9＋3＝20),故含2．但是5＋3＋2＝10是10的倍数,矛盾．

综上所述,n的最小值为5．

割尾法

当我们熟悉了常用数的整除特征后,一个自然的问题是:怎样速判一个正整数能否被7整除?

判断一个正整数能否被7整除,可采用“割尾法”,如对2527割掉末位数字7得到252,再从252中减去被割掉的末位数字7的2倍得到238,这称为一次“割尾”,对238再进行一次“割尾”得到7,显然7是7的倍数,从而2527可被7整除．

在东西方文化中,7是具有神秘色彩的数字,一个星期7天、七色霞光、纯水的pH值、七巧板、七夕之鹊桥相会、哥尼斯堡七桥问题……都关联着7．

七巧板激发了意大利家具设计师丹尼尔·拉格的设计灵感,他将七巧板用于组合书架的设计,创作出极具特色的作品．

例8　试证明:一个正整数被7整除的充分必要条件是对该数有限次“割尾”所得到的数能被7整除．

(河北省竞赛题)

解题思路　从正整数的多项式表示切入．

142857是一个奇妙的数,这个奇妙的数以如下的方式与“7”相约:

142857×2＝285714

142857×3＝428571

142857×4＝571428

142857×5＝714285

142857×6＝857142

142857×7＝999999

请你证明:检验整除性的截尾法．

一个数割去末位数字再加上末位数的2倍,若所得的新数是19的倍数,则原数也是19的倍数．

适当修改上述法则,即可用来检验一个数能否被17整除,读者不妨一试．

1．是能被3整除的五位数,则k的所有可能取值有_________个;这样的五位数中能被9整除的是________．

(“希望杯”邀请赛试题)

2．用写有数字的4张卡片可以排出不同的四位数,其中能被22整除的四位数的和是_________．

(江苏省竞赛题)

3．不超过100的自然数中,将凡是3或5的倍数的数相加,其和为_________．

(全国初中数学联赛题)

4．小学里我们判定一个自然数是否能被3整除,只要看这个自然数的各位数字之和是否能被3整除．现在学了用字母表示数,就可以明白其中的道理啦!以三位数为例,用表示个位数字是c,十位数字是b,百位数字是a的任意三位数,则＝100a＋10b＋c＝(a＋b＋c)＋99a＋9b．如果a＋b＋c能被3整除,设a＋b＋c＝3n(n为自然数),那么＝3(_________),所以能被3整除．

(《时代学习报》数学文化节试题)

5．设七元正整数组(a,b,c,d,e,f,g)满足等式abc＝70,cde＝71,efg＝72,则满足条件的正整数有________组．

(美国数学竞赛题)

6．有_________个形如的五位整数,满足均能被37整除．

(克罗地亚数学奥林匹克试题)

7．下面有五个数:

1234554321,12345543212,123454321,1234543212,123454321×1234554321,其中有(　)个是2009的倍数．

A．0　B．1　C．2　D．3　E．4

(国际中小学数学能力检测题)

8．在1,2,3,…,99,100这100个自然数中,不是2,3,5的倍数的数有k个,则k＝(　)．

A．25　B．26　C．27　D．28

(“希望杯”邀请赛试题)

9．达妮卡开着她的新车走了整数小时,汽车平均时速为55英里．开始时里程表显示数字为,其中,(a≥1,a＋b＋c≤7)为一个三位数,停车时里程表显示数字为,则a2＋b2＋c2＝(　)．

A．26　B．27　C．36　D．37　E．41

(美国数学竞赛题)

10．若15能被15整除,则n的最小值等于(　)．(https://www.chuimin.cn)

A．2　B．3　C．4　D．5

(北京市竞赛题)

11．在体育活动中,七年级(1)班的n个学生围成一圈做游戏,与每个学生左右相邻的两个学生性别不同,则n的取值可能是(　)．

A．43　B．44　C．45　D．46

(山东省竞赛题)

12．设n是小于100的正整数且使2n2－3n－2是6的倍数,则符合条件的所有正整数n的和是(　)．

A．784　B．850　C．1536　D．1634

(全国初中数学联赛题)

13．设a,b,c是正整数,且2c|ab,3a|bc,5b|ca,求abc的最小值．

(爱沙尼亚数学奥林匹克试题)

14．称自然数n为“好数”,应在十进制下满足下列几个条件:

①n是四位数;

②n的第一位和第三位数字相同;

③n的第二位和第四位数字相同;

④n的各位数字的乘积是n2的约数．

试求所有的好数．

(意大利数学奥林匹克试题)

15．如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”．例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”．再如22,545,3883,345543,…,都是“和谐数”．

(1)请你直接写出3个四位“和谐数”,请你猜想任意一个四位“和谐数”能否被11整除?并说明理由．

(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字为x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的关系式．

(重庆市中考题)

16．黑板上写着五个正整数,其中任何三个数的和均可被其余两个数中的每一个整除．问:这五个数中是否一定有四个相等的数?

(俄罗斯数学竞赛题)

17．n是不为0的任意自然数,m是n－1,n,n＋1,n×n＋1这四个自然数的乘积,那么,

(1)m是不是6的倍数?

(2)m是不是5的倍数?

(世界数学团体锦标赛试题)

18．从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?

(《数学周报》杯全国初中数学竞赛题)

19．在1,2,…,2012中取一组数,使得任意两个数之和不能被其差整除．试问:最多能取多少个这样的数?

(北京大学自主招生试题)

例1　8　因1＋4＝2＋3,故1,4排在偶数位,2,3排在奇数位,有4种排法;将2,3排在偶数位,1,4排在奇数位,也有4种排法．

例2　C　关于②的证明:对于a,b,若至少有一个是3的倍数,则ab是3的倍数,若a,b都不是3的倍数,则有:(1)当a＝3m＋1,b＝3n＋1时,a－b＝3(m－n);(2)当a＝3m＋1,b＝3n＋2时,a＋b＝3(m＋n＋1);(3)当a＝3m＋2,b＝3n＋1时,a＋b＝3(m＋n＋1);(4)当a＝3m＋2,b＝3n＋2时,a－b＝3(m－n)．

例4　根据“拷贝数”的定义,得

可知N为99的整数倍,这样的三位数可能是198,297,396,495,594,693,792,891,990．这9个数中,只有954－459＝495,故495是唯一的三位“拷贝数”．

例5　设u＝2x＋3y,v＝9x＋5y．

当x和y是整数时,u和v也是整数．

于是3v－5u＝17x．　①

当2x＋3y能被17整除时,即u能被17整除,由①式,3v能被17整除,又由3和17互素,则v能被17整除,即9x＋5y能被17整除．

当9x＋5y能被17整除时,即v能被17整除,由①式,5u能被17整除,又由5和17互素,则u能被17整除,即2x＋3y能被17整除．

例8　设正整数为,即

A＝10n－1an－1＋10n－2an－2＋…＋10a1＋a0．

经过一次“割尾”后,A变为

A′＝(10n－2an－1＋10n－3an－2＋…＋10a2＋a1)－2a0．

显然有10A′＝A－21a0．

因为10与7互质,可知若A被7整除,则A′也被7整除．反之亦然．所以一个正整数被7整除的充分必要条件是对该数进行有限次“割尾”所得到的数能被7整除．

1．3个,94599　2．10912

3．2418　和为3(1＋2＋…＋33)＋5(1＋2＋…＋20)－15(1＋2＋…＋6)＝2418．

4．n＋33a＋3b

5．96　由cde＝71,c|70,e|72,得c＝e＝1,d＝71,而fg＝72＝32·23,有3×4＝12组正整数解,ab＝70＝2×5×7,有23＝8组正整数解,故满足条件的七元正整数组有12×8＝96组．

由于37|999,若x,y,z中有一个被37整除,则其余两个也被37整除．

因此,所有满足题意的的个数(即相应的37abc的个数)为

7．B　由2009＝72×41,111111＝7×11×13×111,11111＝41×271,得1234554321＝11111×111111是41和7的倍数,但不是72的倍数,123454321＝11111×11111不是7的倍数,故仅有12345543212是2009的倍数．

9．D　设达妮卡开车走了n(n为正整数)小时,则100a＋10b＋c＋55n＝100c＋10b＋a,得9(c－a)＝5n,5|(c－a),(a,b,c,n)＝(1,0,6,9)．

10．B　11．B　学生总数应是4的倍数．

12．D　2|3n,设n＝2m(m为正整数),原式＝6m2－6m＋2(m2－1),3|(m2－1),设m＝3k＋1或m＝3k＋2(k为非负整数),得n＝2m＝6k＋2或n＝6k＋4,故符合条件的所有正整数n的和是(2＋8＋14＋…＋86＋92＋98)＋(4＋10＋16＋…＋82＋88＋94)＝1634．

13．由2c|ab,5b|ca得2c×5b|ab·ac,即2×5|a,同理2×3|b,3×5|c,于是22×32×52|abc,即900|abc,故abc的最小值为900．

14．注意到一个好数n一定具有形式:n＝101(10a＋b)(1≤a、b≤9),因为(ab)2|n2,所以,ab|n2．

又101为质数,则,ab|(10a＋b),故a|b,b|10a．

于是,所有可能如下:

(1)b＝a,则a2|11a⇒a|11,故a＝b＝1．

(2)b＝2a,则2a2|12a⇒a|6,故(a,b)＝(1,2),(2,4),(3,6)．

(3)b＝5a,则5a2|15a⇒a|3,故a＝1,b＝5．

上述每一对数字都决定了一个好数,故所有的好数是1111,1212,2424,3636,1515．

15．(1)设四位“和谐数”个位上的数字为a(1≤a≤9且a为自然数),十位上的数字为b(0≤b≤9且b为自然数),则四位“和谐数”可表示为1000a＋100b＋10b＋a．

∵1000a＋100b＋10b＋a＝1001a＋110b＝11×91a＋11×10b＝11(91a＋10b),

∴1000a＋100b＋10b＋a能被11整除,

即任意一个四位“和谐数”能被11整除．

(2)∵这个三位“和谐数”的个位上的数字为x,十位上的数字为y,

∴这个三位“和谐数”可表示为100x＋10y＋x．

∵100x＋10y＋x＝99x＋11y＋2x－y＝11(9x＋y)＋(2x－y),

又∵这个三位“和谐数”能被11整除,且x,y是自然数,

∴2x－y能被11整除．

∵1≤x≤4,0≤y≤9,∴2x－y＝0．

∴y与x的关系式为y＝2x(1≤x≤4且x为自然数)．

16．一定有四个相等的数．

黑板上的五个数按非降顺序依次记为a≤b≤c≤d≤e．

据题意,知a＋b＋c,b＋c＋d均可被e整除．

则d－a＝(b＋c＋d)－(a＋b＋c)也可被e整除．

注意到,0≤d－a＜d≤e,

故仅当d－a＝0时,e|(d－a)．

这表明,a＝b＝c＝d．

进一步可证明满足题中条件的五个数只有(a,a,a,a,a)和(a,a,a,a,3a)两种形式．

17．(1)(n－1)n(n＋1)是三个连续自然数的乘积,肯定既是2的倍数又是3的倍数,即m是6的倍数．

(2)因为m＝(n－1)·n·(n＋1)·(n×n＋1),①

①中的n仅有5种可能:

n＝5k,5k＋1,5k＋2,5k＋3,5k＋4(其中k是自然数)．

若n＝5k,则①含有因数5;

若n＝5k＋1,则n－1＝5k,故①含有因数5;

若n＝5k＋2,则n·n＋1＝(5k＋2)2＋1＝25k2＋20k＋5＝5(5k2＋4k＋1),①也含有因数5;

若n＝5k＋3,则n·n＋1＝(5k＋3)2＋1＝25k2＋30k＋9＋1＝5(5k2＋6k＋2),①也含有因数5;

若n＝5k＋4,则n＋1＝5(k＋1),①也含有因数5．

综上,可知m是5的倍数．

18．首先,如下61个数:11,11＋33,11＋2×33,…,11＋60×33(即1991)满足题设条件．

另一方面,设a1＜a2＜…＜an是从1,2,…,2010中取出的满足题设条件的n个数,对于这n个数中的任意4个数ai,aj,ak,am,

因为33|(ai＋ak＋am),33|(aj＋ak＋am),所以33|(aj－ai)．

因此,所取的数中任意两数之差都是33的倍数．

设ai＝a1＋33di,i＝1,2,3,…,n,由33|(a1＋a2＋a3),得33|(3a1＋33d2＋33d3)．

所以33|3a1,11|a1,即a1≥11．

由于,故dn≤60,所以n≤61．

综上所述,n的最大值为61．

19．将1,2,…,2012分成(1,2,3),(4,5,6),…,(2008,2009,2010),(2011,2012)这671组．

若取至少672个数,则由抽屉原理知必然有两数属于同一组,不妨设a,b(a＞b),故a－b＝1或2．

当a－b＝1时,(a－b)|(a＋b),矛盾;当a－b＝2时,(a－b)|(a＋b),矛盾．

因此,最多能取671个数．例如,取1,4,6,…,2011这671个数满足题意．