奇数、偶数分类与七年级数学视野

数学的历史并不是具体的历史,而是抽象的历史,是创造思想、发现模式的历史．

这就是数学:她提醒你有无形的灵魂,她赋予她所发现的真理以生命,她唤起心神、澄清智慧,她涤尽我们与生俱来的蒙昧与无知．

左图是不同数字的不同写法,从上到下依次为:印度-阿拉伯数字,巴比伦数字,希腊数字,埃及象形文数字,中国手写体数字,希伯来数字,中国筹算数码,罗马数字,埃及僧侣文数字,玛雅数字,二进制数码．

知能概述

整数按能否被2整除分为两大类:奇数和偶数,奇数与偶数有下列基本性质:

1．奇数≠偶数．

2．两个整数相加(减)或相乘,结果的奇偶性如下所示:

3．若干个奇数之积是奇数,偶数与任意整数之积是偶数;偶数个奇数的和为偶数,若干个偶数的和为偶数．

4．设m,n是整数,则m±n,|m±n|的奇偶性相同．

5．设m是整数,则m与|m|,mn的奇偶性相同．

问题解决

例1　已知三个质数a,b,c满足a＋b＋c＋abc＝99,那么|a－b|＋|b－c|＋|c－a|的值等于_________．

(“希望杯”邀请赛试题)

解题思路　运用奇数偶数、质数合数性质,不断简化已知等式．

整数的简单构成,若干世纪以来一直是使数学获得新生的源泉．

——伯克霍夫

涂色解题

高莫端,当代应用数学家,美国国际商业机器公司(IBM)的研究人员．20世纪60年代,在运筹学“线性整数规划”问题研究上,因提出“割平面法”而闻名．

他曾对下面问题感兴趣．

下图是由14个边长为1的小方格组成的残棋图,你能否把它剪成七块1×2的小长方形?

例2　已知a,b,c三个数中有两个奇数、一个偶数,n是整数,如果s＝(a＋n＋1)(b＋2n＋2)(c＋3n＋3),那么(　)．

A．s是偶数　B．s是奇数

C．s的奇偶性与n的奇偶性相同　D．s的奇偶性不能确定

(江苏省竞赛题)

解题思路　从和的奇偶性来研究积的奇偶性．

例3　假设a1,a2,…,an是数1,2,…,n的某种排列．证明:如果n是奇数,那么乘积(a1－1)×(a2－2)…(an－n)是偶数．

(匈牙利数学奥林匹克试题)

解题思路　转换角度思考问题,化积的奇偶性为和的奇偶性来研究．

例4　设x,y(x≤y)是正整数,且使x2＋y2＝2018成立的(x,y)有多少组?

(“希望杯”邀请赛试题)

解题思路　因方程与整数的平方关联,故需综合运用奇数、偶数、整除等知识,逼近求解．

例5　开始时,5×5方格表中的每个方格中都填有一个0,每一步选取两个具有公共边的方格,将其中的数同时加1或同时减1．若干步后,各行、各列之数的和彼此相等．求证:所经过的步数为偶数．

(俄罗斯数学奥林匹克试题)

证明　若一步中所选的两个方格在同一行,则称为“水平步”,若在同一列,则称为“竖直步”．

在5×5方格表中,考虑第二列之和S2与第四列之和S4．

每一水平步使S2,S4之一加1或减1(即改变±1),另一个不变,故改变S2－S4的奇偶性;每一竖直步使S2,S4不变或改变±2,故不改变S2－S4的奇偶性．

由于开始与结束时均有S2－S4＝0,故水平步数为偶数．

类似的考察第二行、第四行之和,可知竖直步数也为偶数．

所以,总步数为偶数．

对同一个数学对象,从两个方向考虑(n项和与积),再将这两个方向合在一起整体考虑,得出结论,这叫计算两次原理,通过计算两次可以建立方程,证明恒等式等．

应用整数的奇偶性解题,常需变换角度去考察问题,从而化难为易．

设n为整数,偶数可表示为2n,奇数可表示为2n－1或2n＋1．因(2n)2＝4n2,(2n＋1)2＝4n(n＋1)＋1,故可推得奇偶数的如下性质:

(1)偶数的平方被4整除,奇数的平方被4除余1;

(2)奇数的平方被8除余1．

例6　有1997枚硬币,其中1000枚国徽朝上,997枚国徽朝下．现要求每一次翻转其中任意6枚,使它们的国徽朝向相反,问能否经过有限次翻转之后,使所有硬币的国徽都朝上?给出你的结论,并给予证明．

(山西省太原市竞赛题)

解　不能,理由如下:将国徽朝上赋予“＋1”,朝下赋予“－1”,则1997枚硬币的国徽朝向情况可用1997个数乘积表示,若这些数之积为－1(或＋1),表明有奇数(或偶数)枚国徽朝下,开始时,其乘积为(＋1)1000·(－1)997＝－1,每次翻转6枚硬币,即每次改变6个数的符号,其结果是1997个数之积仍为－1,经有限次翻转后,这个结果总保持不变,即国徽朝下的硬币永远有奇数枚,故回答是否定的．

奇偶分析

奇偶性是整数的固有属性,通过分析整数的奇偶性来解决问题的方法叫奇偶分析法．

奇数偶数,是用整数的两种状态来研究整数．

奇偶性与二值状态相应,如电灯开与关、亮与灭,面向南或北,杯口向上与向下,都是两种状态,皆可用奇、偶来描述,用奇偶性来分析．

用染色法或赋值法进行奇偶分析,有时使解题更为直观、简捷．

例7　高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为1cm的正方形,用四个边长为1cm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由．

(汉城国际数学竞赛题)

解　不能,理由如下:因为圆柱侧面是50×50的正方形,将其黑白相间染色,则黑格与白格各有偶数个,又因为每个“T”字形含有3个或1个黑格,若能用“T”字形纸片拼成50×50的正方形,则需要(50×50)÷4＝625个“T”字形,而625个“T”字形含有奇数个黑格,矛盾,因此,不可能拼成．

1．已知整数a,b,c中,a,b的奇偶性不同,且c＝,下面给出4个结论:

①a可能是偶数;②c一定是奇数;③a一定是奇数;④b一定是偶数．

其中,正确的结论是_________．

(《时代学习报》数学文化节试题)

例6通过赋值法,把实际问题转化为数学问题,把抽象的推理转化为具体的计算．

所谓赋值法,就是在解题时,将问题中的某些元素用适当的数表示,然后利用这些数值的大小、正负性、奇偶性等进行推理论证的一种解题方法．

素数是人类追寻知识过程中最无奈的谜题．怎样才能预测下一个素数?有何公式可以生成素数?在素数表面的噪音之下潜藏着意料之外的和谐．1859年,德国数学家黎曼做出一个关于这首“神秘乐曲”的大胆预言,这个预言的答案在电子商务、量子力学和计算机科学等领域产生革命性的影响．

2．数列1,1,2,3,5,8,13,21,34,55,…的排列规律是:前两个数是1,从第三个数开始,每一个数都是它前面两个数的和,这个数列叫做斐波那契数列,在斐波那契数列的前2004个数中共有_________个偶数．

(“希望杯”邀请赛试题)

3．47个不同的自然数的和是2006,这47个自然数中最多有_________个奇数．

(“创新杯”竞赛题)

4．从1,2,3,…,2007中,至少要取出________个奇数才能保证存在两个数,它们的和为2008．

(上海市中学生业余数学学校考试题)

5．A,B,C,D,E,F,G七盏灯各自装有拉线开关,开始B、D、F亮着,一个小朋友按从A到G,再从A到G,又从A到G的顺序依次拉开关,一共拉了2000次,这时亮着的灯是________．

(吉林省竞赛题)

6．在一次象棋比赛中,每两个选手恰好比赛一局,每局赢者记2分,输者记0分,平局每个选手各记1分,今有4个人统计了这次比赛中全部得分总数,由于有的人粗心,其数据各不相同,分别为1979,1980,1984,1985,经核实,其中有一人统计无误,则这次比赛共有_________名选手参加．

(北京市竞赛题)

7．如果a,b,c是三个任意整数,那么(　)．

A．都不是整数　B．至少有两个整数

C．至少有一个整数　D．都是整数

(全国初中数学竞赛题)

8．将连续自然数1,2,3,…,n(n≥3)的排列顺序打乱,重新排成a1,a2,a3,…,an,若(a1－1)(a2－2)(a3－3)…(an－n)恰为奇数,则n(　)．

A．一定是偶数　B．一定是奇数

C．可能是奇数,也可能是偶数　D．一定是2m－1(m是奇数)

(“希望杯”邀请赛试题)

9．a,b,c是三个大于3的质数,则下列判断中一定正确的是(　)．

A．a＋b＋c是偶数　B．a2＋b2＋c2是偶数

C．a＋b＋c是3的倍数　D．a2＋b2＋c2是3的倍数

(“希望杯”邀请赛试题)

10．若正整数a,b,c满足a2＋b2＝c2,且a为质数,那么b,c两数(　)．

A．同为奇数　B．同为偶数　C．一奇一偶　D．同为合数

(“五羊杯”竞赛题)

11．四个学生进行计算比赛,程序是:在19,20,21,…,93,94这76个自然数中,相邻两数之间任意添加“＋”号或“－”号,然后求其代数和．四个人得到的结果分别是1,153,4106,4260．老师检查后指出,只有一个结果是正确的,则这个结果是(　)．

A．1　B．153　C．4106　D．4260

(北京市竞赛题)

12．吉尔最近搬进了新居,房号是一个三位数,这个数与三个位数上的数字之和是429,请问房号三个位数上的数字的乘积是(　)．

A．20　B．28　C．30　D．36　E．48

(英国中学数学竞赛题)

13．设x1,x2,…,xn为＋1或－1,并且x1x2x3x4＋x2x3x4x5＋x3x4x5x6＋…＋xn－3xn－2xn－1xn＋xn－2xn－1xnx1＋xn－1xnx1x2＋xnx1x2x3＝0．证明:n能被4整除．

(国际数学奥林匹克候选题)

14．证明:不存在整数a,b,c,d满足下列等式: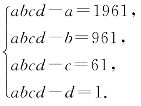

(莫斯科数学奥林匹克试题)

15．在黑板上记上数1,2,3,…,1974．允许擦去任意两个数,且写上它们的和或差,重复这样的操作,直至在黑板上留下一个数为止．求证:这个数不可能为零．

(基辅数学奥林匹克试题)

16．从0,1,…,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”．若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”．问:图①和图②是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由．

(第16题)

(浙江省竞赛题)

17．是否存在正整数x,y,使得x2＋y2＝2016成立?若存在,请求出x,y的值;若不存在,请说明理由．

(北京市竞赛题)

例1　34　a,b,c中必存在偶质数2,设a＝2,推得b＝2,c＝19．

例2　A　(a＋n＋1)＋(b＋2n＋2)＋(c＋3n＋3)＝(a＋b＋c)＋6n＋6为偶数,则(a＋n＋1),(b＋2n＋2),(c＋3n＋3)中至少有一个为偶数,从而s必为偶数．

例3　考虑所有因数ai－i的和．

(a1－1)＋(a2－2)＋…＋(an－n)＝(a1＋a2＋…＋an)－(1＋2＋…＋n)＝0

由于n是奇数,0是偶数,若所有的因数ai－i(i＝1,2,…,n)都是奇数,则奇数个奇数的和应为奇数,不可能为0,出现矛盾．所以必有一个因数ai－i是偶数,从而乘积是偶数．

例4　因2018被4除余2,奇数的平方被4除余1,偶数的平方是4的倍数,故x,y必同时为奇数．又因奇数的平方的个位数必为1,5,9之一,若两个奇数的平方和的个位数为8,则这两个奇数的平方的个位数都应是9,即这两个奇数的个位数为3或7．

又x≤y,则

即

1009≤y2＜2018,

因为312＝961,322＝1024,…442＝1936,452＝2025,

所以32≤y≤44,y的可能值只有33,37,43,列表如下:

因为169＝132,故符合条件的(x,y)仅有(13,43)这一组．

1．②③④　ac＝a＋b,a＋b必为奇数,ac是奇数;a,c都是奇数．

2．668　从第一个数开始,每组连续的3个数中,前两个数是奇数,第三个数是偶数,2004÷3＝668．

3．44　设有a个奇数,(47－a)个偶数,a必为偶数,若a＝46,则1＋3＋5＋…＋91＝462＝2116＞2006,不合题意;若a＝44,则1＋3＋5＋…＋87＝442＝1936,2006－1936＝70,另三个偶数的和为70即可(如2,4,64)．

4．503　将1,2,3,…,2007中所有的奇数按和为2008的两个一组配成502组:(1,2007),(3,2005),(5,2003),…,(1003,1005)．于是至少要取出503个奇数才一定有两个数同组,它们的和为2008．

5．B,D,G　2000÷7＝285……5,说明前5盏灯的开关被拉了286次(偶数次),原来亮着的B,D仍然亮着,后两盏灯的开关被拉了285次(奇数次),原来暗着现在变亮的是G,原来亮着的F现在变暗．

6．45　每局比赛不管胜负如何,双方得分的和为2,从而全部得分总数应为偶数．于是只有1980,1984中的一个正确,设x人参加比赛,则只有×2＝1980,x＝45．

7．C　a,b,c中至少有一个奇数或同为偶数．

8．A

9．D　非3的倍数的数的平方除以3余1．

10．C　a2＝(c＋b)(c－b),a为质数,c＋b＞c－b,则c－b＝1,c＋b＝a2．

11．C　19＋20＋21＋…＋93＋94＝4294为偶数,这76个自然数相邻两数之间任意添加“＋”号或“－”号,其代数和应为偶数,19＋20＋21＋22＋…＋91＋92＋93－94＝4106．

12．B　三个单独数字之和最多是27,因此房号的第一位数是4,第二位数不会大于3．如果第二位数是偶数,那么房号和它的三个单独数字之和会有相同的奇偶性,即两者都可能是偶数,或两者都是奇数,因此,它们两者之和应该是偶数．然而,题中两者之和是奇数,所以,第二位数是1．如果房号的最后一位数是d,那么,410＋d＋(4＋1＋d)＝429,因此,d＝7,房号的三个单独数字的乘积是28．

13．由于乘积x1x2x3x4,x2x3x4x5,…,xnx1x2x3都是＋1或－1,且其总和为0,所以一定有偶数项,即n一定是偶数2m．

将上面的n个数相乘,一方面,其中的＋1和－1各有m个,所以它们的乘积为(－1)m．另一方面,在乘积中,x1,x2,…,xn作为因数都出现4次,所以乘积为＋1．

于是(－1)m＝1,m为偶数,故n是4的倍数．

14．a,b,c,d都是奇数,abcd－a为偶数,不可能等于1961．

15．考虑黑板上保留奇数的个数．

经过一次操作,如果是一个奇数和一个偶数,则由奇数与偶数的和与差为奇数,于是擦去一个奇数和一个偶数得到一个奇数,此时,奇数的个数保持不变．

如果是两个奇数,则由奇数与奇数的和与差为偶数,于是擦去两个奇数得到一个偶数,同样擦去两个偶数得到一个偶数,此时,奇数的个数减少2个或保持不变．

由以上分析知,经过操作,黑板上奇数的个数的奇偶性不变．

由于一开始黑板上共有＝987个奇数,即有奇数个奇数,所以经过若干次操作后,黑板上必须保留奇数个奇数,因而不可能为0．

16．对图①的完美填法不唯一,如图a所示．对于图②不存在完美填法．这是因为图②中共有10条连线,所以,各连线上两数之差的绝对值恰为1,2,…,10,其和S＝|a1－a2|＋|a1－a3|＋|a2－a3|＋…＋|a7－a8|＝55为奇数．

另一方面,图②中每个圆圈均有偶数条连线,即每个圆圈内的数在上述S的表达式中出现偶数次．因此,S应为偶数,矛盾．

从而,图②中不存在完美填法．

(第16题)

17．证明:不存在正整数x,y,使x2＋y2＝2016．

假设存在正整数x,y,使x2＋y2＝2016成立．因为奇数的平方是被4除余1的数,偶数的平方为4的倍数,两个奇数的平方和为被4除余2的数,一个奇数的平方与一个偶数的平方之和是被4除余1的数,只有两个偶数的平方和是4的倍数,而2016是4的倍数,故2016是两个偶数的平方和．即x,y必同时为偶数．

不妨设x＝2a,y＝2b(a,b为正整数)．则有

(2a)2＋(2b)2＝2016,

整理得

a2＋b2＝504．

同理,因为504是4的倍数,故a,b同时为偶数．

不妨设a＝2c,b＝2d(c,d为正整数)．则有

(2c)2＋(2d)2＝504,

整理得,存在正整数c,d,使得c2＋d2＝126成立．因为126被4除余2,故c,d必同时为奇数．

不妨设c≤d,则

故c只能取1,3,5和7．

当c＝7时,d2＝126－49＝77,而77不是完全平方数,故d非正整数;

当c＝5时,d2＝126－25＝101,而101不是完全平方数,故d非正整数;

当c＝3时,d2＝126－9＝117,而117不是完全平方数,故d非正整数;

当c＝1时,d2＝126－1＝125,而125不是完全平方数,故d非正整数．

所以不存在正整数c和d,使得c2＋d2＝126成立．所得矛盾表明,“存在正整数x,y,使x2＋y2＝2016”成立的假设不成立．

综上所述,不存在正整数x,y,使得x2＋y2＝2016成立．