使用一元线性回归进行推测

2025-09-29 理论教育版权反馈

【摘要】：回归方程最有效的用途就是在给定自变量数值x=x0的前提下，推算因变量的数值y=y0。点估计方法是指将自变量数值x=x0代入回归方程，用计算的回归估计值=直接作为因变量y0的估计值。值得注意的是，回归方程只能以自变量x推算因变量y，而不能反过来以因变量y推算自变量x。

回归方程最有效的用途就是在给定自变量数值x=x0的前提下，推算因变量的数值y=y0。按照准确程度，估计分为点估计与区间估计两种方法。

点估计方法是指将自变量数值x=x0代入回归方程，用计算的回归估计值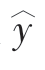 pagenumber_ebook=137,pagenumber_book=124 =直接作为因变量y0的估计值。

区间估计的方法是指以回归估计值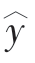 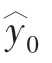pagenumber_ebook=137,pagenumber_book=124 =为基础，得出因变量y0在一定概率保证下可能取值的一个区间。这个区间也叫置信区间。当因变量y为正态分布，且n较大（n≥30）时，置信区间的一般形式为：

其中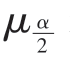， pagenumber_ebook=137,pagenumber_book=124 表示与置信度对应的标准正态概率双侧临界值，其他与前相同。

【例5-6】接【例5-5】，假设同一社区某居民家庭2025年全年可支配收入为11百元，在95%的概率保证下，估计其消费支出。

已知x0=11百元，Syx=3.55百元；当置信度1-α=95%时，临界值 pagenumber_ebook=137,pagenumber_book=124 =1.96（见附录三），则有：(https://www.chuimin.cn)

y0=-0.208 9+0.717 7×11≈7.69（百元）（点估计）

y0=7.69±1.96×3.55≈14.65（百元）

即y0在0.73～14.65百元（区间估计）

这种利用回归方程进行的估计在日常社会经济生活中经常用到，是一种重要的管理工具。值得注意的是，回归方程只能以自变量x推算因变量y，而不能反过来以因变量y推算自变量x。