回归方程最有效的用途就是在给定自变量数值x=x0的前提下，推算因变量的数值y=y0。点估计方法是指将自变量数值x=x0代入回归方程，用计算的回归估计值=直接作为因变量y0的估计值。值得注意的是，回归方程只能以自变量x推算因变量y，而不能反过来以因变量y推算自变量x。......
2023-08-13
一元线性回归模型的估计和检验：应用统计学中的成果
【摘要】：对两个具有线性关系的变量，配合线性回归方程，并根据自变量的变动来测定因变量平均发展趋势的分析方法，称为一元线性回归分析，也称简单直线回归分析。（三）一元线性回归分析的特点两个变量的地位不是对等关系。估计的结果表明，该社区居民月消费支出随可支配收入的增加而增加。估计的结果表明，该地交通事故数随机动车辆数的增加而增加。
在相关图分析的基础上，可以选择一定的回归方程式进行定量分析。对两个具有线性关系的变量，配合线性回归方程，并根据自变量的变动来测定因变量平均发展趋势的分析方法，称为一元线性回归分析，也称简单直线回归分析。它是回归分析中最基本、最常用的方法。
（一）构建一元线性回归方程应具备的条件
一般情况下，构建一元线性回归方程应具备以下几个条件。
1.现象间存在数量上的相互依存关系
只有当两个变量存在比较密切的相关关系时，所构建的回归方程才有意义，用此进行分析和预测才有价值。
2.现象间存在线性相关关系
一元线性回归方程在图形上表现为一条直线。因此，只有当两个变量的相关关系表现为直线相关时，所配合的直线方程才是对客观现实的真实描述，才可用此进行统计分析。如果现象间的相关关系表现为曲线，却配合为直线，就必然会得出错误的分析结论。
3.具备一定数量的变量观测值
一元线性回归方程是根据自变量和因变量的样本观测值求得的，因此，变量x和变量y都应有一定数量的对应观测值，这是构建直线方程的依据。如果观测值太少，受随机因素的影响较大，就不易观察出现象间的变动规律性，所求出的回归方程也就没有意义。
（二）一元线性回归方程
设x为自变量，y为因变量，y与x之间存在某种线性关系，其一元线性回归方程为：
式中，b0和b1是两个待定参数，也称回归系数。其中b0是直线在y轴上的截距，当x=0时，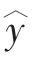
=b0；b1是直线
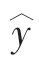的斜率，它表明自变量增加（或减少）一个单位，因变量相应增加（或减少）多少。当b1＞0时，x与y为正相关；当b1＜0时，x与y为负相关。
（三）一元线性回归分析的特点
（1）两个变量的地位不是对等关系。在进行回归分析时，必须根据研究目的确定哪个变量是自变量、哪个变量是因变量。
（2）因变量为随机变量；而自变量为非随机变量，是可以预先给定或控制的变量。
（3）回归方程可以利用自变量的给定值来推算因变量的相应值，它反映的是自变量与因变量之间的具体变动关系。
（4）回归系数b1可正可负，正号说明两变量为正相关；负号说明两变量为负相关。
（四）OLS估计
估计方程的回归系数有许多方法，其中使用最广泛的是最小平方法（Ordinary Least Square，OLS），下面我们采用最小平方法来估计方程的回归系数。
最小平方法的中心思想，是通过数学方程配合一条较为理想的趋势线，这条趋势线必须满足两个条件：原数列的观测值与方程的估计值的离差平方和为最小；原数列的观测值与方程的估计值的离差总和为零。
现以公式表示如下。
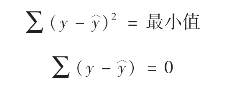
式中，y代表原数列的观测值，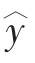
代表回归估计方程的估计值。
，根据极值原理，为使Q具有最小值，对b0和b1分别求偏导数，并令其等于零，即：
整理出两个标准方程：
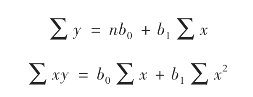
对上面两等式联立求解，解出回归系数b0、b1分别为：
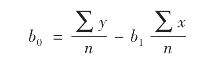
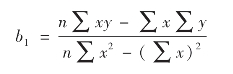
【例5-3】根据表5-2居民家庭的月可支配收入和消费支出的调查资料，进行一元线性回归分析，确定回归方程。
根据消费支出与可支配收入之间的关系，令消费支出为因变量y，可支配收入为自变量x，直线回归方程参数计算如表5-8所示。
表5-8 居民家庭的月可支配收入和消费支出的回归方程参数计算
所以，回归方程为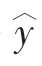
=-0.208 9+0.717 7x
上式说明，该社区2019年居民月可支配收入x每增加100元，消费支出y就平均增加71.77元；在月可支配收入x=0的情况下，消费支出为-0.208 9元。根据这个方程，可以估计该社区居民月可支配收入对消费支出的影响。估计的结果表明，该社区居民月消费支出随可支配收入的增加而增加。
【例5-4】某地近几年机动车辆数与交通事故数的统计资料如表5-9所示。请判断机动车辆数与交通事故数之间是否具有线性相关关系，如果具有线性相关关系，求出线性回归方程。
表5-9 某地近几年机动车辆数与交通事故数统计资料
这里，我们可以借助Excel，根据数据得到散点图，如图5-2所示，直观判断散点在一条直线附近，故具有线性相关性。
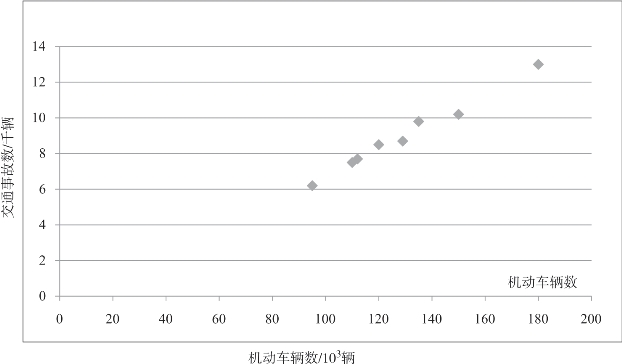
图5-2 机动车辆数与交通事故数的散点图
严格来讲，应先计算出相关系数R，再根据计算结果判断是否可进行回归分析，在相关关系显著的情况下再计算出回归方程，以下为严格的解题过程。
根据交通事故数与机动车辆数之间的关系，令交通事故数为因变量y，机动车辆数为自变量x，相关系数计算如表5-10所示。
表5-10 机动车辆数与交通事故数的相关系数计算
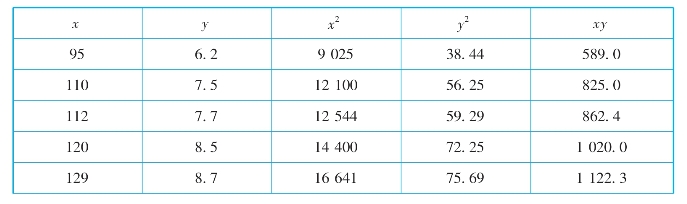
续表
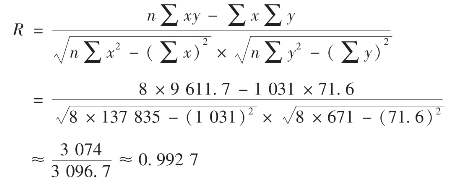
计算结果说明，交通事故数与机动车辆数之间存在高度正相关关系。所以，x和y线性相关关系显著，可进行回归分析。
再依据表5-10中的数据，可以计算出b1和b0，进而得到线性回归方程。
所以，回归方程为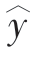
=-1.024 1+0.077 4x
上式说明，该地近几年机动车辆数x每增加1 000辆，交通事故数y就平均增加0.077 4千辆。根据这个方程，可以估计该地机动车辆数对交通事故数的影响。估计的结果表明，该地交通事故数随机动车辆数的增加而增加。
有关应用统计学的文章
- 详细阅读
-
生态数据分析：多元线性回归的假设检验详细阅读
，βm不全为零在H0成立条件下，有由上述统计数F进行F检验即可推断多元线性回归关系的显著性。［例6］对［例5］所建立的二元线性回归方程进行假设检验。表7-2二元线性回归方差分析表二、偏回归系数的假设检验上述多元线性回归关系假设检验是检验各自变量共同对因变量的线性影响是否显著。因此，当多元线性回归关系显著时，还必须逐一对各个偏回归系数进行假设检验，发现并剔除对因变量的线性影响不显著的自变量。......
2023-11-17
-
一元线性回归回顾-基于R实验详细阅读
回归分析的基本思想和方法以及“回归”名词的由来，要归功于英国统计学家高尔顿（Galton）．高尔顿和他的学生、现代统计学的奠基者之一皮尔逊（Pearson）在研究父母身高与其子女身高的遗传关系时，观察了1 078对夫妇，以每对夫妇的平均身高作为x，而取他们的一个成年儿子的身高作为y，将这些数据画成散点图，发现趋势近似一条直线＝33．73＋0．516x（单位：英寸，1英寸＝2．54 cm）．这表明：......
2023-11-18
-
应用统计学：估计标准误差详细阅读
估计标准误差也称剩余标准差、回归标准误差，是剩余变差的平均数的平方根。估计标准误差以回归直线为中心，反映各观测值与估计值之间的平均离差程度，用来说明直线回归方程代表性大小的统计分析指标。估计标准误差就是进行这种检测的统计分析指标。估计标准误差的计算方法主要有两个，一个是定义公式，一个是简捷公式。在实践中，在已知直线回归方程的情况下，通常用下面的简捷公式计算估计标准误差。估计标准误差计算如表5-11所示。......
2023-08-13
-
多元统计分析：线性回归方程的确定和影响检验详细阅读
，Xp 来表示．在回归分析中，主要研究以下问题：确定Y 与X1，X2，…，Xp 之间的定量关系表达式，这种表达式称为回归方程；对所得到的回归方程的可信程度进行检验；判断自变量Xi（i＝1，2，…，p）对因变量Y 有无显著影响；利用所求得的回归方程进行预测或控制．......
2023-11-18
-
生物统计实训：一元线性回归应注意问题详细阅读
回归分析和相关分析已广泛运用于动物科学类专业的科研工作中，但是却很容易被误用或对结果作出错误的解释。如果不以一定的生物科学依据为前提，把风马牛不相及的资料随意凑到一块作回归或相关分析，那将是根本性的错误。就是说，要考虑到回归系数、相关系数等这些统计数的适用范围。一个显著的线性相关系数或回归系数亦并不意味着x和y的关系必为线性，因为它并不排斥有能够更好地描述x和y关系的非线性方程的存在。......
2023-10-30
-
回归概念与种类-应用统计学详细阅读
（一）回归的概念回归最初是遗传学中的一个名词，是由英国生物学家兼统计学家高尔顿首先提出来的。“回归”这一名词，从此便一直为生物学和统计学所沿用。回归的现代概念与过去大不相同。在线性回归方程中，因变量与自变量的关系是直线型的，例如，耐用消费品销售量与居民货币收入的关系。在非线性回归方程中，因变量与自变量的关系是曲线型的，例如，某商店的商品流通费用率与销售额的关系。......
2023-08-13
-
应用统计学中的统计学学派详细阅读
在这个时期，不同学派的学术观点已经形成，并且形成了两个主要学派，即数理统计学派和社会统计学派。这是社会统计学派的显著特点。但是，社会统计学派仍然强调在统计研究中必须以事物的质为前提，这同数理统计学派的计量不计质的方法论性质是有本质区别的。......
2023-08-13
相关推荐