在这个时期，不同学派的学术观点已经形成，并且形成了两个主要学派，即数理统计学派和社会统计学派。这是社会统计学派的显著特点。但是，社会统计学派仍然强调在统计研究中必须以事物的质为前提，这同数理统计学派的计量不计质的方法论性质是有本质区别的。......
2023-08-13
应用统计学：常用变异指标
【摘要】：常用的变异指标有全距、平均差、方差、标准差、变异系数、偏度和峰度系数。这些变异指标的值不仅与数据本身的变异程度有关，也受数据量纲和计量单位的影响。变异系数又称为离散系数，它是各种变异指标与同组数据的算术平均数对比得到的相对数，反映该组数据的相对离散程度，通常用百分数表示。最常用的是标准差系数。
常用的变异指标有全距、平均差、方差、标准差、变异系数、偏度和峰度系数。
（一）全距（极差）
全距是一组数据中最大值与最小值之差，反映了数据值在这组数据中的最大波动程度或范围。因为全距是这组数据中两个极端值之差，所以又称为极差，一般以R表示，其计算公式为：
R=xmax-xmin
式中，xmax为该组数据中的最大值，xmin为该组数据中的最小值。
显然，全距只受两个极端值的影响，无法反映数据组的内部差异，对数据变异程度的测定是相当粗略的。但是由于计算简便，可以用来快速分析数据的离散程度。
【例4-19】某班5名同学身高分别是161cm、162cm、179cm、168cm、165cm，则该班同学身高的全距是多少？
该组身高最大值是179cm，最小值是161cm，所以全距是179-161=18（cm）。
（二）平均差（平均绝对离差）
平均差，又称为平均绝对离差，是一组数据中各个数据到其算术平均数离差的绝对值的算术平均数。它综合反映了整组数据的变异程度，利用了全部的数据信息，因而比全距更能客观全面地反映数据的离散程度。平均差越大，则数据离散程度越大，反之则离散程度越小。其基本的计算公式如下。
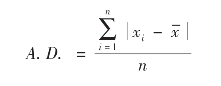
虽然平均差比全距更能全面反映数据整体的离散程度，但由于公式中加入了绝对值符号，在数学上处理起来不方便，在实践中并不常用。
（三）方差
方差是测度数据差异程度最为重要、最为常用的指标。由于平均差的绝对值符号不好处理，利用平方的方法去掉绝对值符号，平均差就变成了方差，即各个数据到其算术平均数离差的平方的算术平均数。对总体而言，方差记为σ2，其公式如下。
式中，N是总体规模，μ是总体的均值。
对样本数据x1，x2，…，xn而言，样本方差记为S2，计算公式如下。
式中，n是样本容量，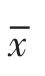
是样本均值。
对于组距式分组资料，方差的计算基本思路和式（4-1）与式（4-2）一样，只是此时需要用各组的频数作为权重来计算加权平均数。
（四）标准差
方差虽然避免了平均差的绝对值符号的问题，但是带来了一个新问题，即其结果将数据的计量单位变成了平方形式，缺乏实际意义。为了解决这个问题，就有了将方差取正的平方根的办法，即标准差，此时其计量单位就变得和原始数据或平均值一样了。
对总体而言，标准差为：
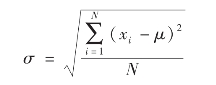
对样本而言，标准差为：
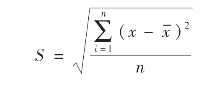
【例4-20】甲、乙两种水稻试验品种连续5年的平均单位面积产量如表4-6所示，试根据这组数据估计哪一种水稻品种的质量比较稳定。
表4-6 甲、乙两种水稻试验品种连续5年的平均单位面积产量 吨
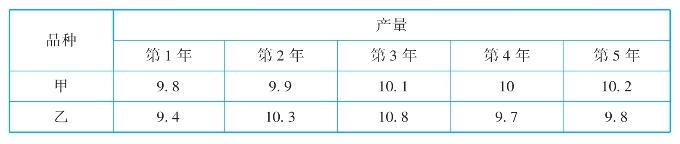
经计算甲、乙两种水稻产量的平均数都是10，要研究水稻品种质量的稳定性，则需要分别计算甲、乙两种水稻产量的方差。
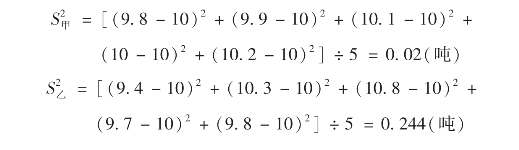
因为0.244＞0.02，所以，甲种水稻的产量比较稳定。
【例4-21】为了保护学生的视力，教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如表4-7所示，试估计这种日光灯的平均寿命和标准差。
表4-7 日光灯使用情况
为计算方便，用每一区间内的组中值作为相应日光灯的使用寿命，分别是：165.5，195.5，225.5，255.5，285.5，315.5，345.5，375.5。由此算得平均数约为：165.5×1%+195.5×11%+225.5×18%+255.5×20%+285.5×25%+315.5×16%+345.5×7%+375.5×2%=268.4≈268（天）
这些组中值的方差为：
×[1×（165.5-268.4）2+11×（195.5-268.4）2+18×（225.5-268.4）2+20×（255.5-268.4）2+25×（285.5-268.4）2+16×（315.5-268.4）2+7×（345.5-268.4）2+2×（375.5-268.4）2]=2 128.60
故所求的标准差为
同样，对于上述计算，我们可以借助Excel中的函数，可用“VARP”和“STDEV”计算方差和标准差，但是该题中每一区间的组中值出现次数不同，类似于加权，在运用Excel函数计算时需要做一些调整。
具体做法为：先将组中值和对应的权数输入表格A1至B8中，在C1格中输入“=A1*B1”，点击“回车”键，即出现结果1.655。选中该格，出现“+”时下拉至C8，可以得到每格的数据。在C9格中输入求和函数“=SUM（C1∶C8）”，点击“回车”键后就得到平均数为268.4。将该数值填入D1至D8，接着在E1中输入“=（A1-D1）^2”，点击“回车”键后得到数据10 588.41。鼠标放至该格，待出现“+”时下拉，依次可得D2至D8的数据。同理，F1至F8的数据则是E格数据与对应B格数据的乘积，然后同样用求和函数计算“=SUM（F1∶F8）”，就得到了F9格中显示的方差值了。最后的标准差则是应用平方根函数“SQRT”对F9计算一下就可以。具体计算结果如图4-4所示。
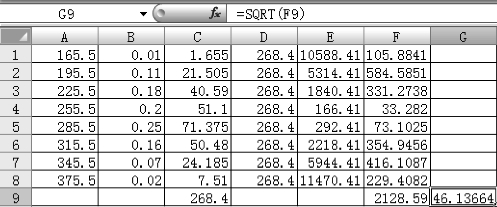
图4-4 日光灯平均寿命与标准差计算结果
（五）变异系数
上面介绍的各种变异指标，包括全距、平均差和标准差，都是用绝对数表示的指标，它们均与原始数据或平均值有着相同的计量单位，也可以称为数据的绝对差异程度指标。这些变异指标的值不仅与数据本身的变异程度有关，也受数据量纲和计量单位的影响。在统计实践中，如果要比较多组数据的离散程度的差异，若各组数据的计量单位和量纲不一样，平均水平也不一样，就不能直接采用上述绝对变异指标来衡量，这时必须采用相对变异指标（即变异系数）来进行分析。
变异系数又称为离散系数，它是各种变异指标与同组数据的算术平均数对比得到的相对数，反映该组数据的相对离散程度，通常用百分数表示。例如，平均差与算术平均数对比得到平均差系数，标准差与算术平均数对比得到标准差系数。最常用的是标准差系数。
对总体数据而言，标准差系数为
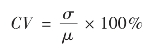
式中，σ是总体标准差；μ是总体均值。
对样本数据而言，标准差系数为：
式中，s是样本标准差；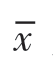
是样本均值。
【例4-22】某班有5名同学，其身高分别以米（m）和厘米（cm）为单位计量。试计算两种情形下的平均差、方差、标准差和变异系数，试比较两种计量单位情形下的离散程度。
（1）以米（m）为单位的身高：1.50、1.60、1.70、1.80、1.90。
（2）以厘米（cm）为单位的身高：150、160、170、180、190。
计算第（1）组数据。
首先，5名同学的平均身高是：
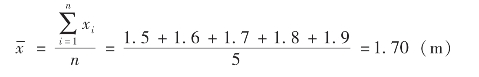
因此，平均差是：
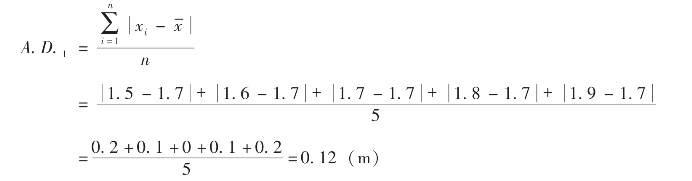
方差是：
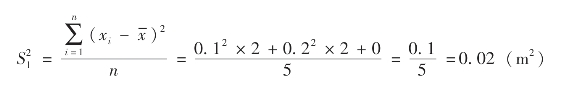
标准差是：
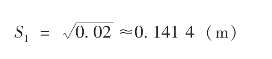
变异系数是：
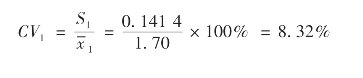
类似地，可以计算得到第（2）组数据各项指标。
均值：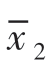
=170（cm）
平均差：A.D.2=12（cm）
方差：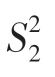
=200（cm2）
标准差：S2=14.14（cm）
变异系数：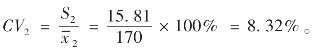
从上述计算结果可以看到，对于同一组数据，计量单位不一样，其平均差和标准差的数值就相差100倍，而方差更是相差10 000倍。如果用这些绝对变异指标来比较不同计量单位的同一组数据的离散程度，就会得出差异程度也相差百倍或万倍的错误结论。而此时如果使用变异系数，就会发现变异系数消除了计量单位和量纲的影响，两种计量单位情形下，变异系数取值完全一样，说明其离散程度本质是一样的。
以上标准差等几种变异指标是从指标数值的角度反映一组数据值的差异程度，但无法反映数据形成的次数分布（总体分布或经验分布）的形状特征，如偏斜程度和陡峭程度，下面引入偏度和峰度系数两个指标。
（六）偏度
一组数据的分布数列中，如果频数分布是完全对称的，则称为对称分布；如果不完全对称，则称为非对称分布或偏态分布。反映数据统计分布偏斜方向和程度的指标即为偏度。
偏态分布有左偏分布和右偏分布两种，这是相对于对称分布而言的。在三种分布类型中，它们的算术平均数
、中位数Me和众数M0有着一定的关系。具体而言有以下几种情形，如图4-5所示。
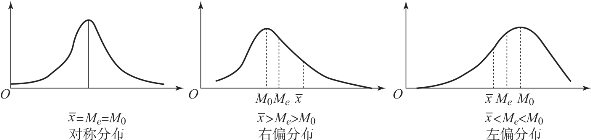
图4-5 对称分布与偏态分布
（1）对称分布时，有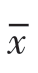
=Me=M0。
（2）右偏分布时，有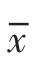
＞Me＞M0。
（3）左偏分布时，有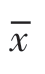
＜Me＜M0。
偏度的测定有多种方法，这里简单介绍利用算术平均数与众数进行比较得到偏度的方法。
如上述，在非对称分布中，算术平均数、中位数和众数相互分离，中位数一般位于二者之间，此时算术平均数与众数的距离就可以用来测定偏度，即：
这是偏度的绝对量，若为正值，则为右偏分布；若为负值，则为左偏分布；若为零，则为正态分布。偏度绝对值越大，说明偏斜程度越大。但是不同的数据分布，其计量尺度不一样。若要比较偏斜程度，用绝对偏度并不恰当，需要偏度系数这个相对指标，即偏度除以数据的标准差，通常以SKP表示，计算公式为：
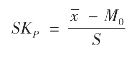
（七）峰度系数
峰度系数是用来衡量数据分布的集中程度或分布曲线的尖耸程度的指标，计算公式为：
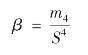
式中，
称为四阶中心动差，S是样本数据标准差。
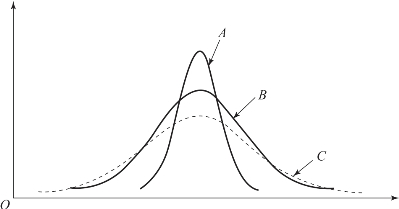
图4-6 不同峰度的分布曲线
衡量数据统计分布的集中程度或分布曲线的尖耸程度是以标准正态分布为参考的。标准正态分布曲线的峰叫正态峰，对应的峰度系数β=3，如图4-6中的B分布曲线所示；若某分布计算出来的β＞3，表示分布曲线的形状比标准正态分布要更陡峭、更集中，称为尖顶峰，如图4-6中的A分布曲线所示；若某分布计算出来的β＜3，表示分布曲线的形状比标准正态分布要更平缓、更分散，称为平顶峰，如图4-6中的C分布曲线所示。
由于偏度和峰度的计算较复杂，本章仅建议掌握偏度和峰度的概念及计算公式。
有关应用统计学的文章
- 详细阅读
-
现金流控制常用参考指标详细阅读
对现金流量进行控制，可以企业经营活动现金净流量为核心，建立一套企业现金流量控制指标体系，与现金流量预算相互配合，从而实现对现金流量有效、动态的控制。现金流量结构指标有经营现金流入量与现金总流入量之比、经营活动现金流入量与经营活动现金流出量之比等。因而，将现金流量比率控制在一定范围内，对于防范企业的偿债风险、提高企业的偿债能力具有较大的意义。......
2023-08-24
-
内存储器分类及常用指标详细阅读
在计算机内部，直接与CPU交换信息的存储器称为“内存储器”，简称“内存”，用来存放计算机运行期间所需的信息，如指令、数据等。1）内存的分类按照存取方式，内存可以分为随机存储器和只读存储器两大类。DRAM的特点是集成度高，必须定期刷新才能保存数据，所以速度较慢，通常用作主存；SRAM的特点是存取速度快，制造成本高，主要用作高速缓冲存储器。图2.6存储单元的地址和内容衡量内存的常用指标有存取速度和存储容量。......
2023-10-22
-
应用统计学|统计学发展历史|Null详细阅读
统计作为一种社会实践活动，已有悠久的历史。在统计学的发展过程中，至少经历了以下三个发展阶段。威廉·配第用数字、重量和尺度将社会经济现象数量化的方法作为近代统计学兴起的重要特征，他将统计学领入了搜集数据和分析数据的新时代。在政治算数阶段出现的统计与数学的结合趋势逐渐发展形成了统计分析科学。“统计分析科学”课程的出现是现代统计发展阶段的开端。......
2023-08-13
-
应用统计学-调查问卷案例详细阅读
案例一大学生租房意愿调查亲爱的同学们，你们好！我们正在做一项关于大学生租房意愿的调研，此次调研完全匿名，也不会做其他的商业用途，全部完成问卷将花费5～10分钟时间，我们期待您的宝贵意见！案例二购房喜好情况调查今年，您会选什么样的房子？请在你所选答案编号处打“√”，或按题目要求填写问卷，于××年××月××日前将有效答卷邮寄至本报物业版，按邮戳标明日期的先后顺序，前50名读者将可获得本报半年期赠阅卡。......
2023-08-13
-
生态数据分析与建模：常用统计学术语详解详细阅读
常用希腊字母表示，例如用μ表示总体平均数，用σ表示总体标准差等。实际上，统计学关心的是总体参数的大小，其依据是统计量及其性质。为了便于处理实际问题，统计学中常用若干典型的分布模式来近似的描写实际资料，如正态分布、二项分布和泊松分布等，常称为统计模型。利用统计模型进行统计分析可以简化运算。......
2023-11-17
-
《应用统计学：高效方案设计》详细阅读
数据搜集的主要形式是统计调查，它是一项复杂的工作。要做好统计调查，必须按照统计研究的目的，运用科学的方法，有组织、有计划地进行。统计调查方案的设计包括以下步骤。确定调查对象必须明确总体界限，划清调查范围，区别应调查和不应调查的对象。在实际工作中，调查单位与报告单位密切相关，调查单位是调查的承担者，而报告单位是负责上报调查资料的单位。......
2023-08-13
-
应用统计学-统计特点和作用详细阅读
（一）统计的特点统计作为人们认识客观世界总体数量变动关系和变动规律活动的总称，具有以下特点。这是统计学区别于其他社会经济科学的根本特点。（二）统计的作用1.统计是认识世界的有力武器人们通过统计研究事物的量及其变化，去认识事物的质和事物发展的规律。......
2023-08-13
相关推荐