应用统计学：数值数据图形展示

2023-08-13 理论教育版权反馈

【摘要】：也就是说，条形统计图中，横轴上的数据是孤立的，是一个具体的数据；而直方图中，横轴上的数据是连续的，是一个范围。最后，条形图主要用于展示品质数据，直方图则主要展示数值数据分布情况。在应用方面，直方图通常适用于大批量数据，茎叶图通常适用于小批量数据。图3-13全国及湖北省外新冠肺炎累计确诊病例增速折线图散点图用点的密集程度和变化趋势来表示两指标之间的直线相关关系。图3-14某校10名女大学生身高与体重数据散点图

以上介绍的品质数据的图示方法——条形图、饼图也都适用于数值型数据。但数值型数据还有以下一些特定的图示方法，这些方法并不适用于品质数据。

（一）分组数据：直方图

直方图是针对分组资料，以横轴表示变量、纵轴表示该组的具体数值，用条状的图形来表示其数值分布情况的图形。图3-8是根据表3-7所示的小明班上统计学考试成绩分布情况绘制的直方图。

表3-7　小明班上统计学考试成绩

pagenumber_ebook=70,pagenumber_book=57

续表

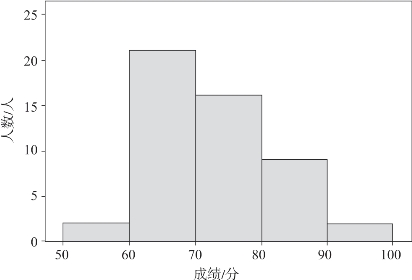
pagenumber_ebook=71,pagenumber_book=58

图3-8　小明班上统计学考试成绩分布情况的直方图

【小思考】直方图与条形图是一回事吗？

【例3-5】为了了解某校1 800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况，在全校范围内随机抽取了若干名学生，对他们最喜爱的体育项目（每人只选一项）进行了问卷调查，将数据进行了统计，并绘制成了如图3-9所示的统计图。请问该图是直方图吗？

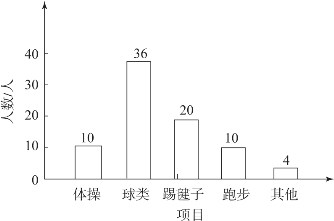
pagenumber_ebook=71,pagenumber_book=58

图3-9　全校课外体育项目喜爱情况

图3-9中横轴上表示的仅是体育项目的类别，不是同一类数据的分组，图中各长方形之间有空隙，且长方形的高表示的是喜爱各类体育项目的人数，显然这是条形图，不是频数分布的直方图。

【例3-6】某同学对本班某次捐款情况进行了统计，全班50人共捐款900元。该同学分别绘制了如图3-10所示的条形统计图（注：每组含最小值，不含最大值）。这个说法正确吗？

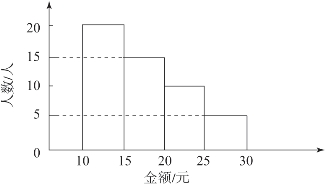
pagenumber_ebook=72,pagenumber_book=59

图3-10　捐款金额及人数分布统计

根据题意可知，图3-10中横轴上表示的是学生捐款金额的分组，它们是连续的，并且题中指出每组含最小值，不含最大值，这就表明这组数据是连续排列的，中间没有空隙。因此，图3-10表示的是频数分布直方图，而不是条形图，把它称为“条形统计图”显然是错误的。

直方图与条形图的主要区别有以下几点。

首先，条形图是用条形的长度表示各类别频数的多少，其宽度（表示类别）则是固定的。而直方图矩形的高度表示每一组的频数或频率，宽度则表示各组的组距，其高度与宽度均有意义。

其次，由于分组数据具有连续性，直方图的各矩形通常连续排列，而条形图则分开排列。也就是说，条形统计图中，横轴上的数据是孤立的，是一个具体的数据；而直方图中，横轴上的数据是连续的，是一个范围。

最后，条形图主要用于展示品质数据，直方图则主要展示数值数据分布情况。

【小思考】请问根据表3-8资料所作的如图3-11所示的直方图合理吗？

表3-8　某小区4—5月感冒患者年龄分布

pagenumber_ebook=72,pagenumber_book=59

续表

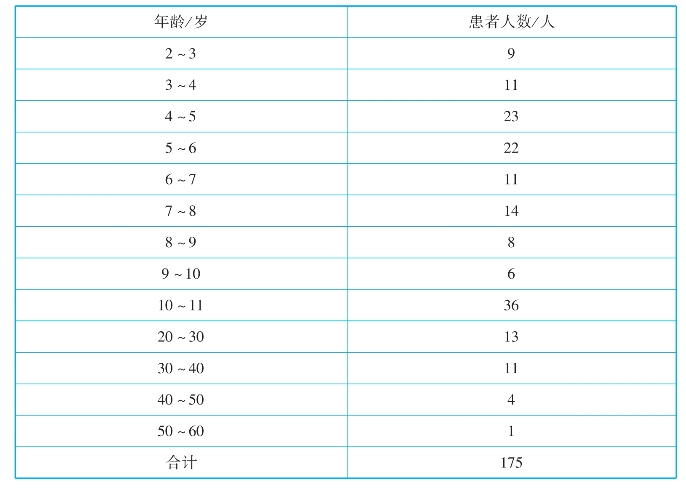
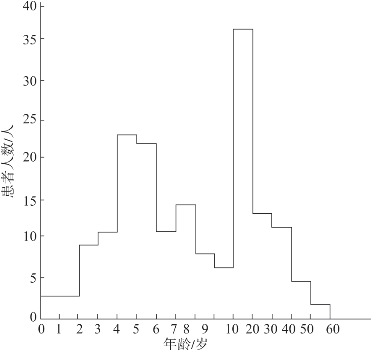
pagenumber_ebook=73,pagenumber_book=60

图3-11　某小区4—5月感冒患者年龄分布直方图

（二）未分组数据：茎叶图

茎叶图又称枝叶图，它的绘制思路很形象，也很具体化，概括起来就是将数据按位数进行比较。将数的大小基本不变或变化不大的位数作为一个主干（茎），将变化大的位数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面有几个数、每个数具体是多少。例如，125分成12|5，12分成1|2，等等，前部分是茎，后部分是叶。

茎叶图类似于横置的直方图，与直方图相比，茎叶图既能给出数据的分布状况，又能给出每一个原始数值，即保留了原始数据的信息。而直方图虽然能够很好地显示数据的分布，但不能保留原始的数值。在应用方面，直方图通常适用于大批量数据，茎叶图通常适用于小批量数据。

【例3-7】图3-12是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图。在这几场比赛中，甲、乙两人的最高分分别是多少？

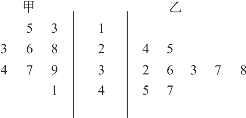
pagenumber_ebook=74,pagenumber_book=61

图3-12　甲、乙运动员每场比赛得分茎叶图

由所给的茎叶图可知，甲的得分是13分、15分、28分、26分、23分、39分、37分、34分、41分，这组数据的最高值是41分；乙的得分是24分、25分、32分、36分、33分、37分、38分、45分、47分，这组数据的最高值是47分。因此，甲、乙两人的最高分分别是41分和47分。

（三）时间序列数据：折线图

如果数值型数据是在不同时间取得的，即时间序列数据，则可以绘制折线图。折线图主要用于反映现象随时间变化的特征。图3-13是2020年1月25日至2月10日全国及湖北省外新冠肺炎累计确诊病例增速折线图。可以看出，全国累计确诊病例增速明显放缓，连续三天处于10%以下；湖北省外地区的累计确诊增速进一步下降至3.51%，疫情扩散势头得到控制。

（四）多变量数据：散点图

以上介绍的一些图形描述的都是单变量数据。当有两个或两个以上变量时，可以采用多变量的图示方法，常见的有散点图、雷达图等。

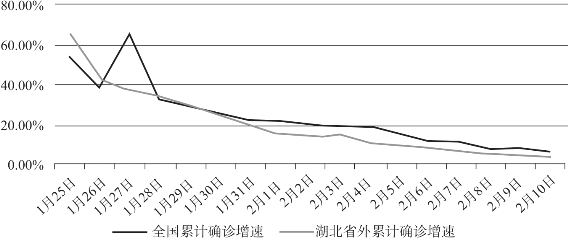
pagenumber_ebook=75,pagenumber_book=62