当今教育家们较一致的看法是：数学教学方法是为达到数学教学目的，实现教学内容，运用教学手段而进行的以教师为主导、学生为主体的师生相互作用的活动。既然教学方法是以儿童的学习规律为依据，以学生学习规律为依据选择的教学内容，就自然成了教学方法的依据。因此，一般而言，教学内容决定教学方法。反之，教学方法一旦选定之后，却并不仅仅是被动的，会对教学内容产生重大的反作用。......
2023-08-12
数学建模：意义与方法，高中数学教学方法研究与实践
【摘要】：高中数学课程通过设立数学建模的学习活动，正式将它作为实现这一理念的重要途径。高中数学课程应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系，促进学生逐步形成和发展数学应用意识，提高实践能力。
（一）数学建模的意义
简而言之，用数学语言和方法设计数学模型的过程称为数学建模。新课程标准指出：“数学建模是运用数学思想、方法和知识解决实际问题的过程，已经成为不同层次数学教育重要和基本的内容。”
关于在高中阶段开展数学建模活动的意义，新课程标准主要是从发展学生的数学应用意识和将数学建模作为一种新的数学学习方式两个方面来论述的。二者的意义都在于突出体现高中新课程的基本理念。
第一，新课程标准将数学建模作为促进学生逐步形成和发展数学应用意识，提高实践能力的重要途径。发展数学应用意识，提高实践能力是新课程标准倡导的一个重要课程理念。高中数学课程通过设立数学建模的学习活动，正式将它作为实现这一理念的重要途径。正如新课程标准中关于课程的基本理论第5条所说：20世纪下半叶以来，数学应用的巨大发展是数学发展的显著特征之一。当今知识经济时代，数学正在从幕后走向台前，数学和计算机技术的结合使得数学能够在许多方面直接为社会创造价值。同时，也为数学发展开拓了广阔的前景。我国的数学教育在很长一段时间内对于数学与实际、数学与其他学科的联系未能给予充分的重视。因此，高中数学在数学应用和联系实际方面需要大力加强。近几年来，我国大学、中学数学建模的实践表明，开展数学应用的教学活动符合社会需要，有利于激发学生学习数学的兴趣，有利于增强学生的应用意识，有利于扩展学生的视野。
高中数学课程应提供基本内容的实际背景，反映数学的应用价值，开展数学建模的学习活动，设立体现数学某些重要应用的专题课程。高中数学课程应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系，促进学生逐步形成和发展数学应用意识，提高实践能力。
第二，新课程标准倡导数学建模是一种新的数学学习方式。新课程标准倡导积极主动的、勇于探索的学习方式。高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识。新课程标准在数学建模的内容中指出：“数学建模是数学学习的一种新的方式，它为学生提供了自主学习的空间，有助于学生体验数学在解决实际问题中的价值和作用，合乎实际，体验数学与日常生活和其他学科的联系，体验综合运用知识和方法解决实际问题的过程，增强应用意识；有助于激发学生学习数学的兴趣，发展学生的创新意识和实践能力。”
高中数学课程设立数学建模学习活动，通过该活动的组织开展，它将与数学探究活动一起，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯。
（二）数学建模的方法
自然界的事物五花八门、千姿百态，其发展变化也非常复杂。所以，给自然界的事物建模并没有一个固定的模式。数学建模是一个系统的过程，它要利用许多技巧以及翻译和解释、分析与综合、计算及证明等高度的认知活动。因此，建模是一种十分复杂的创造性劳动。
新课程标准中提出了数学建模可以通过以下框图体现。
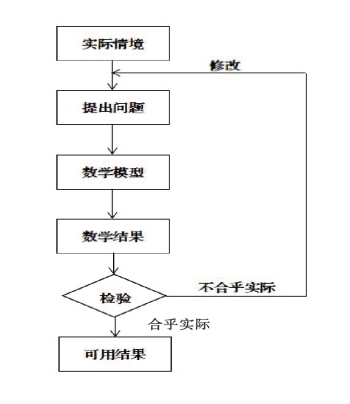
图3-1 数学建模流程图
根据新课程标准中数学建模的方法步骤，下面给予说明和进一步描述。
实际情境。这是建模前的准备工作，即建立数学模型之前，必须理解实际问题的情境，掌握所要解决问题的有关背景知识和数据资料等信息，从实际问题的特定关系和具体要求出发，找出影响实际问题的重要因素，牢固掌握有关数学知识和方法。此外，还应明确建立模型的目的。
提出问题。建立数学模型是对实际问题进行具体分析的科学抽象过程，要在对实际问题进行分析的基础上，进行抽象、提出问题，这是一个化繁为简、化难为易的过程。因此，要抓住问题主要矛盾的主要方面，舍弃次要方面，猜测重要因素之间的关系，进行简化，这是建模的关键一步，简化假设要适度，否则会对建模产生不良影响。
建立数学模型。在假设的基础上，利用适当的数学方法来表示问题各数量之间的关系，建立相应的数学模型。
模型求解。对数学模型进行计算，得出数学结果，进行模型分析。建模以后，对模型进行数学解答。
模型检验。将模型的结果运用到实际问题的解决中，运行模型，对模型的结果与实际相互比较，以便检验模型的可靠性和准确性，对不符合实际的情况要进行修改，进一步提出问题。
可用结果。符合实际的结论，就是可用的结果，数学模型被接受之后，进入实际应用阶段，在实际应用中应该不断地改进模型。
有关高中数学教学方法研究与实践的文章
- 详细阅读
-
高中数学教学方法研究与实践成果详细阅读
《全日制义务教育数学课程标准》注重培养学生的创新精神和实践能力，建立新的教学方式，促进学习方式的变革，突出学生个性化的发展。新课程标准强调教学过程是师生交往、共同发展的互动过程。要在实践中学习、使学习成为在教师指导下主动的富有个性的过程。由于每一个学生都是一个特殊的个体。因此，教师必须首先将学生看成是有个性的学习者，承认差异、尊重差异、善待差异。......
2023-08-12
-
高中数学教学方法研究与实践：传统的数学教学方详细阅读
在我国中学数学教学的长期实践中，形成了各种不同的教学方法。因为这些方法历史悠久，因此被人们称为传统的教学方法。体态语包括手势、身势、表情、眼神等，是传递信息、增强语言表达效果的手段。所以，它也是目前中学数学教学中最为普遍采用的一种教学方法，特别是侧重于数学思想和方法以及能力培养的课题，在教学时宜采用讲练结合法。......
2023-08-12
-
高中数学教学方法研究实践详细阅读
在高中数学教学过程中，教师可以通过结合生活化的教学方式来帮助学生理解抽象、有难度的数学内容。在高中数学教学中，为了帮助高中生更好地学习和掌握数学知识内容，教师要学会优化相关的教学结构，从教学目标、教学内容以及教学方法三个方面进行更加细致化的教学。教师与学生之间通过搭建起合作探讨学习知识的桥梁，激发高中生的求知欲，进而推动高中数学学习的效率。......
2023-08-12
-
高中数学教学方法的研究与实践成果详细阅读
新的数学课程标准的出台和实施，促进了数学教师本身的成长，为教师的发展提供了广阔的天地和空间。根据数学课程标准的基本理念，学生的学习方式将发生变化，这对数学教师的教学工作提出了新要求。从课前准备、教学内容的安排、数学活动的组织到教学方法的运用等，都需要重新设定。在教学活动中，主要的工作有以下六项。如《全日制义务教育数学课程标准》中的组织教学可参照如下。......
2023-08-12
-
高中数学教学方法研究与实践—措施详细阅读
（五）分层教学每个学生的学习程度不尽相同，教师要分析学生的学习程度，对学生进行分层教学。分层教学使每个学生都能接受到适合自己的教学内容，每个学生都能学有所得。（六）注重初高中衔接教师要重视初高中的衔接，了解学生的学习情况、学习能力以及学习方法等。数学教学对于学生的全面发展有着重要的影响，高中阶段的数学学习更是有其存在的重要价值。......
2023-08-12
-
高中数学教学方法研究实践成果详细阅读
传统的数学教材与教法过于偏重形式，强调逻辑思维能力，忽视数学灵感和创造性，过于偏重演绎论证的训练。在当前全面推进以培养创新精神和实践能力为重点的素质教育进程中，应该对诸如数学实验等非逻辑化的数学方法和教学方法给予重新认识，注重实验、直觉、形象思维等非逻辑地揭示知识的形成发展过程。实际的数学教学忽视人文教育的倾向，已经引起有关方面的高度重视。......
2023-08-12
-
高中数学知识特性-高中数学教学方法的研究与实详细阅读
而且教师在教学中也引入了很多问题情境式的教学内容，让师生共舞，以促进学生主动学习，这是现代高中数学的一大特性。（一）知识量广阔性相对于初中数学来说，高中数学在知识量上是一个剧增的量，是数学知识的湖泊，是丰富多彩的现实生活和物质世界的量化知识，也是将具体的物质抽象化了的数量知识。由此可知，利用思维导图进行高中数学教学，不仅适合高中数学知识学习的特点，也说明了在高中数学教与学中引入思维导图的可行性。......
2023-08-12
相关推荐