模型参数敏感性分析结果

在基于多主体建模过程中，通俗来讲，敏感性分析（Sensitivity Analysis）就是看模型的输入参数的取值如何影响模型的输出变量的值。而在模拟复杂系统中的模型时，输出结果往往具有内在的不确定性（Uncertainty）。因此，无论是从理论上来讲，还是从实际操作角度来看，敏感性分析与不确定性分析（Uncertainty Analysis）是难以确切分开的两个过程（Ginot et al，2007），但两者又有各自的不同。简单来说，不确定性分析主要集中讨论输入参数取值的不确定性如何影响输出参数取值的不确定性；而敏感性分析的核心就是要弄清楚每一个输入参数对于模型的输出结果的重要性的大小，也就是要找到哪些输入参数对所关心的研究问题重要，哪些不重要（Helton，2008）。本节主要讨论敏感性分析的问题。

根据分析的对象的不同，敏感性分析通常可以分成两种类别：全局敏感性分析（Global Sensitivity Analysis）和局部敏感性分析（Local Sensitivity Analysis）。全局敏感性分析就是将输入参数作为一个整体并且在关注各个参数之间的相互关系的条件下，分析输入变量空间的变化对输出结果变动的影响。局部敏感性分析就是不考虑各个输入参数之间的相互关联关系，而研究其中的某一个参数的变动对输出结果的变动的影响（Nsoesie et al，2012）。在实际操作过程中，是采用全局敏感性分析还是采用局部敏感性分析取决于敏感性分析的具体目的。全局敏感性分析可以分析出所有输入参数的相对重要性大小，但是这种方法的最大不足就是会大大增加计算机的运算时间，特别是输入参数较多时其需要的运行时间会呈指数级增长。局部敏感性分析只能逐步确定各个参数对输出结果是否有重要影响，而各个参数的相对重要性无法获得，其优点就在于所需要的运算时间较全局敏感性分析而言会大大减少（Wang et al，2008）。本书采用了局部敏感性分析主要基于如下考虑：① 局部敏感性分析的方法适用于线性系统和非线性系统；② 本模型基于大量实际数据，笔者对案例了解比较透彻，并且对相关参数与输出结果的相互关联有一定的掌握，因此可以比较容易地找到对研究问题具有关键意义的参数，不需要对所有参数与所有输出变量的关系一一作出分析；③ 就本书来说，需要关心的是输入参数对于模型输出结果而言的重要性，而不是这些变量对某一个输出结果而言相互之间的相对重要性；④ 本书只需要定性地弄清楚各个参数对输出结果是否重要，而不需要得到重要性的具体定量数据；⑤ 模型的输入参数较多（大于10个），这也预示着如果采用全局敏感性分析将造成不必要但非常高的计算机运行所需的时间成本［因特尔i7等级CPU的一般个人电脑运行一次模型（120步，行为主体数量处于中间水平时）所需要的时间为3～4个小时，10个参数就表示至少需要3×210个小时（不考虑优化的全局敏感性分析可以采用的特殊算法），即大约需要128天才能完成全局敏感性分析所需要实施的模型运行，还没有考虑模型数据分析所需要的时间］。

开展局部敏感性分析方法多种多样，例如微分分析法（Differential Analysis）、响应表面分析法（Response Surface Methodology）、蒙特卡罗分析法（Monte Carlo Analysis）和方差分解过程分析法（Variance Decomposition Procedures）等（Helton，2008）。如上文所述，本书不需要获得各参数的定量重要性，因此本章并没有采用上述数学或统计学等定量方法。参考“序列二叉树法”（Sequential Bifurcation）的基本思路（Bettonvil et al，1997），本章的局部敏感性分析按如下操作步骤进行：① 首先确定要检验其敏感性的一个输入参数，将其值设置为最小极值；② 在被检验参数取最小值的情况下，保持其他输入参数的值不变，将模型运行30次，记录模型运行稳定后（60步后）各个输出变量的平均值；③ 将需要检验的输入参数的取值设为最高值，保持其他输入参数的取值不变，将模型再次运行30次，记录模型运行稳定后各输出变量的平均值；④ 将输入参数取最小值时输出变量的值与输入参数取最大值时的输出变量的值相比较，计算其差值百分比；⑤ 如果该差值百分比大于某一差值百分比水平，那么我们假设该参数对模型的某一输出变量来说具有重要作用，否则可以认为该参数对该输出变量不具有重要性。

1）地理要素参数的敏感性分析

在第5章，已经介绍了模型采用了14个地理参数来定义城市土地空间。为了减少计算机运算所需时间，本书不对自然地理要素（河流、湖泊和山丘）的敏感性进行检验。这是因为，在实际案例中这些要素均属于天然形成，一般不会发生改变（除非大规模人为改造），因此检验其敏感性的实际意义不大。本书着重研究那些源于人类活动而形成的地理要素（城市道路、大型公园绿地、地铁、工业园、大学、衰败的小区、衰败的工厂、购物中心、郊区住房地产和文化便利设施）。其实际意义在于：如果研究显示某一输入参数所对应的地理要素对我们关注的某一输出结果具有重要影响，那么通过改造（改进）该输入参数所涉及的地理要素，可以使我们关注的输出结果朝较好的方向发展。另外一个参数“cloverleaf”也没有进行检验，原因在于根据社会调查研究的结果，该参数对创意企业和创意工人来说均没有显示出重要性。

表6.6列出了检验“城市道路”（Road-Density）这一参数的敏感性时得到的数据。通过这些数据，我们可以看到模型稳定后系统容纳的创意企业的数量、创意工人的数量以创意产业行业的就业率均没有发生较大变动，相应的系统的总产出也没有发生较大变动（变动幅度为0.5%，可以认为是随机误差的结果），因此我们可以看出这些输出变量对城市道路密度这一输入参数的变动的敏感性较弱。进一步，我们也可以看到城市地块价格（办公租金价格和住房租金价格）对城市道路密度的变动也没有表现出明显的敏感性。

观察关于创意企业和创意工人的空间集聚特点的统计量（参见表6.6中的“创意工人的空间集聚”），可以看到该输出统计量对城市道路密度的变动也没有表现出明显敏感性。但是，数据显示，城市道路密度的变动对创意企业和创意工人的空间分布具有较大影响③。在“创意工人的空间分布”一行，数据{-13%; -7%; 9%; 15%}表明，当城市道路的密度增加时（在本模型中，表现为外市区和内郊区城市道路数量的增加），有大量创意工人从城市CBD和内市区迁入外市区④。同样地，根据数据序列{9%; 15%; -7%; -3%}，我们可以判断也有创意工人从内郊区迁入外市区。

表6.6　对城市道路密度参数（“Road-Density”）敏感性的分析

续表6.6

注：表格中各个输出变量的取值为系统稳定后（60步后）的平均值。

类似地，创意企业的空间分布受到道路交通密度变动的影响也发生较大的改变，并且创意企业的空间分布变动趋势与创意工人的空间变动趋势表现出类似性质：随着道路密度的增加，有大量创意企业迁入外市区。不同的是，在CBD范围内，创意企业的数量表现出上升趋势。产生这一不同的原因可能在于“租金价格”对两者的重要性存在明显差异。对创意企业而言，“交易氛围”和“企业之间的邻近性”的重要性均大于“租金价格”，“租金价格”在影响创意企业区位选择的8个因素中排第六位。而对创意工人来说，“租金价格”的重要性则排在第三位（在“道路交通”和“日常购物方便性”之后）。因此，CBD地区较高的价格对创意企业来说影响力并不大，因此也不能明显限制创意企业的进入，而对创意工人来说CBD的高租金价格则具有巨大影响。

上述研究结果表明，在外市区范围内投资建设和提升道路交通服务（公交服务），将更有效率。换句话说，从吸引创意企业和创意工人的角度考虑，将改进城市道路交通服务（公交服务）的资金投入在外市区比投入在内市区和郊区具有更高的边际效用。这也表明，将投资和改进道路交通的焦点置于内郊区将会造成有限的政府预算使用的低效。

采用检验“城市道路密度（road-density）”的相同方法，可以对剩下的地理要素参数的敏感性分别进行检验。表6.7直接给出了采用上述方法得出的结论。从表中可以看出，该模型中所涉及的社会经济子系统的相关输出变量（总产出、创意企业总数、创意工人总数、就业率、住房租金价格的空间分布和办公租金价格的空间分布）对输入的地理要素参数的取值变动没有表现出明显敏感性。然而，其他与地理空间相关的输出统计量对输入的地理要素参数取值的变动表现出明显敏感性，但与创意企业相关的统计量和与创意工人相关的统计量对同一输入参数表现出不同的敏感性。具体来说，部分与决定创意工人区位选择因素相关联的参数（“old-housing-num”“dailyshopping”“suburban-housing”和“culture-num”）的取值变动，仅对与创意工人相关的输出统计量（创意工人的空间分布与创意工人的空间集聚）具有明显影响；对应地，也有另一部分与决定创意企业区位选择因素相关联的参数（“ind-park-num”和“old-factory-num”），仅对与创意企业相关的输出统计量（创意企业的空间分布与创意企业的空间集聚）具有明显影响。

表6.7　地理要素参数的敏感性分析结果

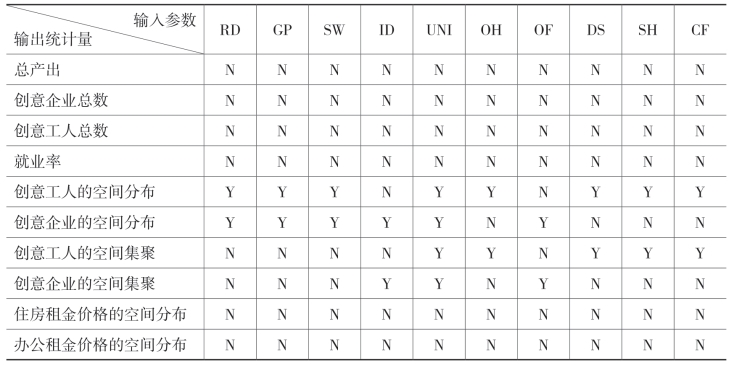
注：（1）RD=“road-density”，GP=“green-park-number”，SW=“subway-number”，ID=“ind-parknum”，UNI=“univ-etc-num”，OH=“old-housing-num”，OF=“old-factory-num”，DS=“dailyshopping”，SH=“suburban-housing”，CF=“culture-num”。参见第5章用户界面图5.4。（2）在表格中，“N”表示不敏感，“Y”表示敏感。

2）政策包参数的敏感性分析

在模型界面上，有3个参数定义了政策包（图5.8），分别为政策包数量（“policysupport”）、政策包的平均有效期（“mean-tenure”）和政策包配发的重点地区（“prior-area”）。参数敏感性分析表明3个参数的取值变动对输出结果都具有明显影响，但不同输入参数所影响的输出变量不同（表6.8）。首先来看“prior-area”这一参数⑦，结果表明只有“行为主体（创意企业和创意工人）的空间分布”这一输出变量表现出了明显的变动。当将“prior-area”的值设定为“内市区（inner urban area）”时，有64%的创意企业分布在CBD和内市区。相比之下，城市内郊区外围和外郊区的创意企业的数量则占到26%。如果将“prior-area”的值设定为“外郊区（outer suburb）”，其结果是内郊区外围和外郊区的创意企业总数占到38%，而相应的城市CBD和内市区的创意企业所占比例则下降到30%。由于创意企业的迁入会提升其周边地块（包括其所在的地块）的建筑质量，而创意企业的迁出则又会降低周边地块（包括其所在的地块）的建筑质量，因此创意企业这一空间分布的变动模式也对创意工人的空间分布变动模式形成一定影响：创意工人的空间分布也表现出类似的空间变动特征。从这个意义上看，我们可以认为将支持性政策作为一种调控手段来发展特定地段的策略具有明显的有效性。

表6.8　定义政策包的参数的敏感性分析

续表6.8

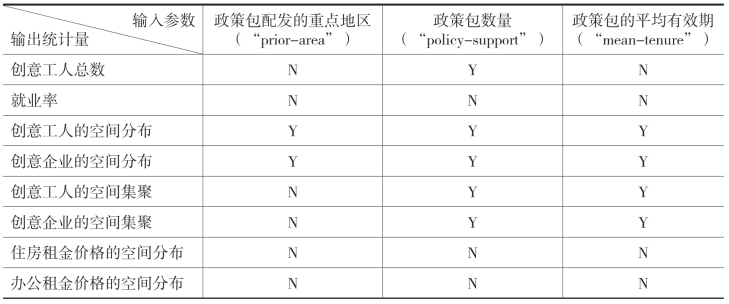
注：“Y”表示敏感，“N”表示不敏感。

进一步检验发现参数政策包数量（“policy-support”）不仅显著影响行为主体的空间分布，还影响行为主体的数量和空间集聚特点。在敏感性分析过程中，一个令人意想不到的情况就是：当将政策包数量设置到较低水平时（也就是说城市政府提供相对较少的政策支持），系统稳定后创意企业和创意工人的总数却比政策包数量设置为较高的情境下的相应的行为主体的数量要多。更有意思的是：当政策包数量较少时，重点支持的地区（在本次模型检验实验中设定为“内郊区”）所吸引的创意企业的数量占到总数的61%；而当政策包数量设定为较高水平时，内郊区吸引的创意企业的数量占总数的比例却下降到52%。根据上述实验结果，似乎可以有如下结论：当城市政府政策支持越少时，创意产业的发展将会越好。然而，根据生活经验，这一结论与现实生活的观察和经验存在明显矛盾（至少直观感受上存在矛盾）。

为了弄清楚其内在的真正逻辑和机制，我们将关注焦点转移到了政策包的平均有效期（“mean-tenure”）上。通过实验，我们发现造成上述具有误导性结论的关键在于政策包的平均有效期被设置过低（上述实验中其值被设定为24，相当于两年）。当我们将该有效期设置为最高值60（相当于5年）时，再重复上述实验，其结果是政策包数量较多时，相应的创意企业数量和创意工人数量也随之增多。因此，对产生上文具有误导性的实验结果可以作出如下解释：当一个企业迁入一个受到政策支持的地块后，其将享受诸如减税、低办公租金等益处。而较短的政策支持则表示这些支持性政策极有可能在该企业还没有足够成长（例如已经雇佣足够的创意工人、获得较好的产品市场等）之前（因为政策支持到期）就被撤除。这些支持性政策的撤除将使得企业的经营成本瞬间大幅度上升，特别是受到的支持力度较大的企业。这一瞬间的成本上升将对企业的生存状态造成致命打击，因此也会造成许多类似企业很快夭折。这一分析机制，在分析政策包的平均有效期（“mean-tenure”）的过程中也得到了验证。当我们将“mean-tenure”的值从24改变到60时，两种情况下运行的结果是创意企业的总数上升了44%，同时创意企业和创意工人的空间集聚强度也均上升了7%。上述实验表明：在实施支持性政策的过程中，必须对政策的有效期作出合理有效的设计，否则越多数量的支持政策可能预示着越差的效果和越大的资源浪费。

3）创意产品的基准需求及其增长率敏感性分析

对模型输入参数创意产品的基准需求“base-product-demand”（第5章图5.9）的敏感性分析表明，该参数几乎对模型的所有输出参数都具有较明显影响。这是因为，在模型中产品的基准需求（假设增长率为0）实际上是规定了整个系统的创意企业允许生成的总的创意产品的数量。创意企业的产出归根结底是创意企业雇佣的创意工人的产出的总体表现，而每一个创意工人的产出能力都有一定限度（模型中假设其服从正态分布）。因此，规定了基准需求，也就相当于规定了系统可以容纳的创意企业和创意工人的最大数量，因此，不可避免地将对整个模型的输出变量造成影响。通过计算基准需求（增长率为0）与系统稳定后的产出的皮尔逊相关系数，可以发现其平均值高达0.96，表明两者之间的确存在非常紧密的关联关系。

根据上述逻辑关系，我们也可以迅速理解创意产品需求月增长率“demand-monthlygrowth-rate”和增长率的变动周期“growth-rate-cycle” （第5章图5.9）均对模型所有输出参数有明显影响。具体来说，当月需求增长率取正值时，系统稳定后对应的行为主体的总数逐步上升；当该参数取负值时，系统稳定后对应的行为主体的总数表现出逐步下降的趋势。而当增长率的变动周期大于0时，整个系统的输出变量的取值则表现出了更大的波动性。

4）定义行为主体行为规则的阈值的敏感性分析

对关系到行为主体的行为的阈值（参见第5章图5.10）进行敏感性分析显示，这些阈值各自均对模型的部分输出变量有较为明显的影响。首先，如果阈值参数与创意工人的行为规范有直接关联关系，其取值的变动对创意工人的影响强于对创意企业的影响，也就是说与创意工人相关的输出变量的变动幅度大于与创意企业相关的输出变量的变动幅度。类似地，如果阈值参数与创意企业的行为规范有直接关联关系，其对创意企业的影响强于对创意工人的影响。其次，根据阈值参数是否与行为主体的区位行为相关，可以将这些参数分成两组，分别称为“区位行为相关的阈值参数”和“非区位行为相关的阈值参数”。敏感性分析的结果显示，“区位行为相关的阈值参数”对行为主体最后表现出来的空间分布和集聚特征的影响强于对行为主体自身基本属性的影响，而“非区位行为相关的阈值参数”对行为主体自身的基本属性以及系统的行为主体数量具有明显的影响（表6.9）。

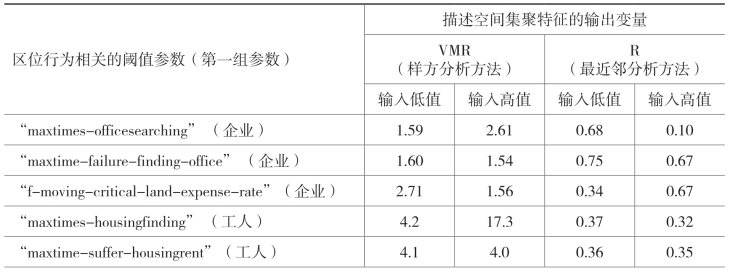
表6.9　阈值参数的敏感性分析

续表6.9

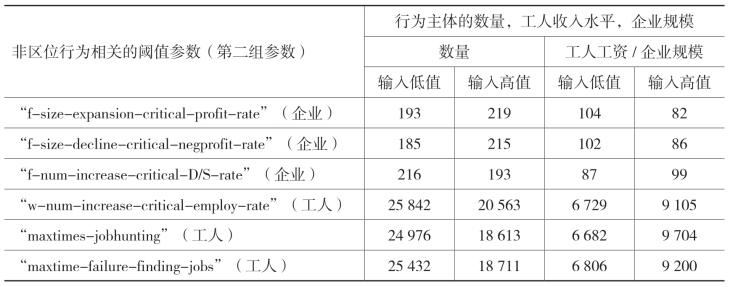
表6.9列出了敏感性分析实验的相关数据。在第一组数据中，当创意企业每月寻找办公区位时所允许的最大尝试次数增加时（相当于假设其能够获得的信息量增加），统计创意企业的空间集聚特征的变量VMR的值随之增大，而统计变量R则相应减小。这表明，当创意企业每月获得的关于住房租赁市场的信息增加时，其将表现出更强的空间集聚特点。在检验参数“maxtimes-housingfinding”上，创意工人的空间集聚也表现出相同的变动趋势。然而，对创意企业而言，当办公租金成本与销售额之比（“f-moving-critical-landexpense-rate”）增加时，空间集聚趋势则表现出减弱趋势。形成这一结果的原因可以作如下解释：允许较高的比率的潜在影响在于企业一旦选定区位后，其因为地价上涨原因被迫离开的概率大大降低，相应地也使得整个系统所包含的创意企业可以尝试寻找合适区位的总次数减少，进而使得集聚的概率大大降低。

与上述情况不同的是，对创意企业和创意工人而言，当寻找办公区位时允许的最大失败次数（“maxtime-failure-finding-office”）和寻找住房区位时允许的最大失败次数（“maxtime-suffer-housingrent”）增加时，其相应的空间集聚的变动并不明显。按照逻辑推理，当这两个阈值增加时，每一个行为主体尝试寻找合适区位的次数则相应增加，因此对整个系统而言行为主体发生空间集聚的概率应该上升，宏观上行为主体应该表现出空间集聚增强的趋势，但实验结果却是集聚趋势的变动并不明显。通过比照分析此间实验的其他数据，发现当两个阈值增大时，创意企业和创意工人的数量却发生相应减少的现象（创意企业数量从256下降到181，创意工人数量从24 793下降到22 332）。行为主体数量的减少，实质上造成了整个系统行为主体空间集聚概率的下降。其基本逻辑是：当阈值增加时，每个行为主体可以尝试空间集聚的次数有所增加，与此同时行为主体的数量的减少则又使得集聚次数发生下降，从而使得所有行为主体能够尝试空间集聚的总次数（平均每个行为主体能够尝试的次数与行为主体总数的乘积）的改变幅度大大降低，从而使得行为主体总体上表现为集聚趋势的变动相对较弱。

再看表6.9中的第二组参数的敏感性检验。结果显示，当把就业率作为一种劳动力市场信号时，在高阈值设定的情况下，系统稳定后创意工人的数量较少，而工人的平均工资水平则较高，这一结果基本符合总需求不变的设定条件（总需求不变，也就表示总供给的变动幅度较低，这是因为系统稳定后两者的比值应该为预设的固定值1）。此外，实验过程中还发现，当创意工人允许找工作连续失败的时间增长时，工人的平均工资水平表现出了增长趋势。产生这一结果的原因在于：允许较长的失败时间则预示着所有工人都有更多的机会参与市场竞争，根据企业在招聘时会选择生产能力较高（相应的工资水平也较高）的工人，而在解雇工人时会优先解雇生产能力较低的工人这一基本规则，生产能力较低的工人被解雇（并被系统剔除）的概率就大大上升，从而造成工人的总体工资水平上升。这一实验结果表明，当创意工人遭遇就业困难时，如果城市政府对所有创意工人在此困难时期采取同样的支持政策（例如给予基本生活补助使其度过困难），那么其结果将会造成工资水平较低的创意工人在未来生活中陷入困境（找不到工作）。因此，从扶持创意工人的角度来看，城市政府应该对收入较低的创意工人给予更多的职业培训，从而提升其在劳动力市场的竞争能力。而如果对所有创意工人一视同仁地采取纯粹的资金补助，则有可能加剧低收入创意工人的就业困难。

与就业率作为劳动力市场信号相类似，系统的实时需求供给比率则用来作为潜在的创意企业是否会进入该系统的信号。也就是说，当实时的需求供给比大于阈值时，新的创意企业将会诞生。如表6.9第二组数据所示，当这一阈值从低值更换到高值后，系统最终的创意企业的数量则相应减少。这是因为当阈值较高时，新企业进入系统的概率将大大降低，反过来也就提高了已有企业雇佣更多创意工人的机会，进而提高企业的实际规模，因此相对来说企业的数量将相应减少（企业平均产出与企业总数的乘积约等于总需求，而总需求为不变的定值）。研究分析进一步发现，如果允许创意企业在较低的利润率下就可以扩展公司规模，或者允许企业在利润率为负时仍然可以继续经营，那么企业的平均规模有上升趋势。上述结果表明，在一个自由市场的环境下，创意企业的规模有增大趋势，也就是说最终的创意产业领域将以大型企业为主。因此，在总需求不变的条件下，也预示着小型企业的数量将日趋减少。这是因为创意企业规模的扩展将会使得创意工人从其他小型企业向大型企业流动，进而迫使小型企业无法招聘到合适的创意工人而破产。通过这些结论，我们可以判断，如果城市政府要想扶持中小型创意企业（从而能够为不同学历背景的劳动力提供多样化的就业机会，并进一步提高就业率），就必须根据中小型企业的发展需求，提供相应的优惠与支持；而“一刀切”式的支持，将不利于中小企业的生存与发展。