(一) 干预前后学生用眼习惯和用眼行为改变各条目的分布情况EFA模拟结果显示，将用眼习惯改变和用眼行为改变两个因子分别进行混合模型潜在类别模拟，模型拟合信息指数结果如表5-4所示。性别、学习成绩、周末参加辅导班、每天做作业时间和教做眼保健操的干预方式仅对干预前有影响，差异有统计学意义。其中居住地和视力检查成正相关，干预前相关系数分别为0.253和0.477，干预后相关系数分别为0.258和0.515。......
2023-08-09
青少年视力不良防治实践：干预效果的因素分析
【摘要】：EFA主要用来初步确定因子个数、指标与因子的关系及因子与因子的关系。探索性因素分析示意图如图5-2所示。从干预效果条目EFA模型拟合指数的结果看，4因子模型的χ2、AIC、BIC和aBIC值均最小，而TLI和CFI值最大。图5-3 探索性因素分析碎石图
探索性因素分析(exploratory factor analysis，EFA)是用于解释外显变量之间相关的统计模型，可解释指标间的相关性和简化数据，即采用几个潜变量(因子)来解释一组变量之间的相关性，当潜变量被抽取后条目之间将不存在相关性，即达到局部独立性(local independence)。EFA主要用来初步确定因子个数、指标与因子的关系及因子与因子的关系。EFA的研究假设是指标间存在相关，是因为有一个潜在的共同因子或公因子(common factor)，如果这个公因子被提取，那么指标间的关系将不存在。在因子分析中，将观测分数的差异分为三个部分：公因子、独特性和测量误差。因素分析的表达式为
Zij=aj1fi1+aj2fi2+…+ajmfim+djuij
其中，Zij为个体i在项目j上的标准分；f为公因子；aj为每个公因子的权重，即因子负荷；uij为独特性因子；dj为独特性因子的权重。探索性因素分析示意图如图5-2所示。
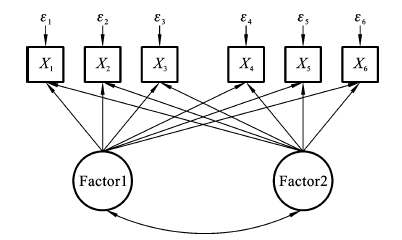
图5-2 探索性因素分析示意图
将调查问卷所涉及的干预效果评估的题目进行探索性因素分析，以期找到几个不同的因子，结果如表5-2、表5-3和图5-3所示。从干预效果条目EFA模型拟合指数的结果看，4因子模型的χ2、AIC、BIC和aBIC值均最小，而TLI和CFI值最大(分别为0.887和0.936)。但是碎石图显示折点在两个因子，提示可能2因子模型比较合适，再结合表5-3的因子负荷矩阵发现，2因子模型对各条目的聚合效果比较好。从具体条目的实际意义来看，条目1~10可归纳为干预前后学生用眼习惯和卫生的改变，而条目11~18可归纳为干预前后行为的改变。
注：*P<0.05。
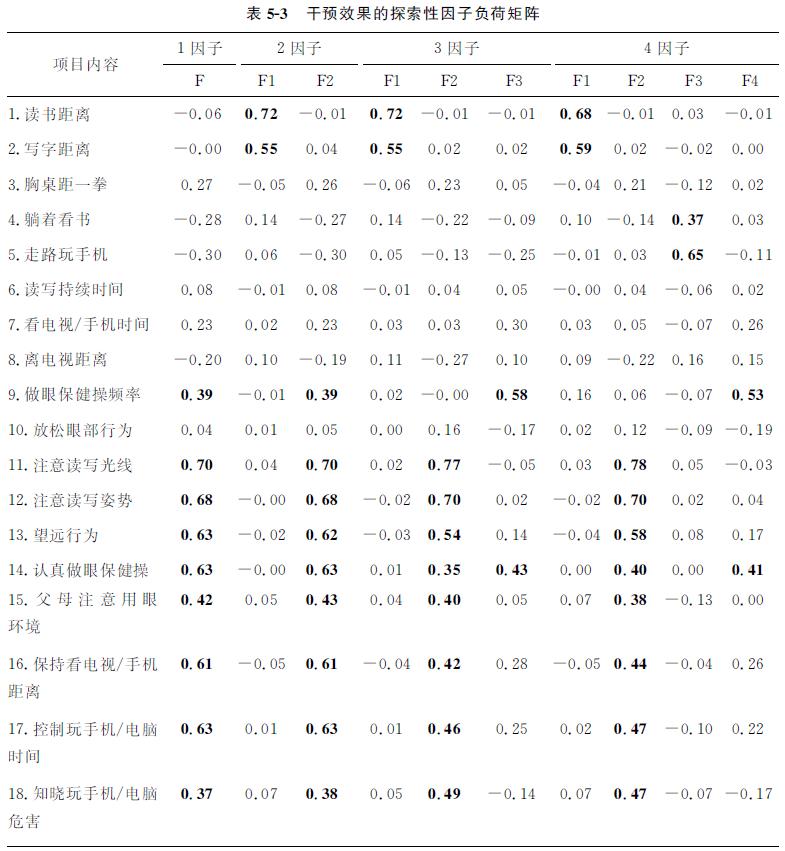
注：因子负荷大于0.30的被加粗。
图5-3 探索性因素分析碎石图
有关青少年视力不良防治的实践与创新的文章
- 详细阅读
-
潜在转换分析与青少年视力不良防治详细阅读
潜在转换分析是潜在类别分析的扩展，是混合分布模型的一种。潜在类别概率和转移概率的预测可以使用Logistic回归直接并入LTA，如分组变量。LTA是以人群为导向的，个体被分为不同的亚组，是在潜在类别分析基础上的项目反应模式。注：P是转换概率，如P12代表第一个潜在类别在时间t时向在t+1时的第二个潜在类别转换的概率。LTA模型是横断面潜在类别分析的纵向应用。......
2023-08-09
-
青少年视力不良防治实践: 抽样街道及学校情况详细阅读
(一) 抽样街道及学校情况1. 抽样街道结果通过采用Excel随机数字法，在每个分区中随机抽取1个街道。具体抽样时，考虑到着重观察小学年龄阶段的效果，因而小学生与中学生的抽样比例设定为2∶1。......
2023-08-09
-
青少年视力不良防治的实践与创新成果详细阅读
(二) 德国德国作为医疗大国，青少年近视率不足15%。该协会经常深入学校，对幼儿园、中小学的学生进行视力跟踪调查，定期检查学生视力，建立青少年视力档案，发现视力降低者及时进行检查、矫正。并且每年推出青少年视力报告，全面评估德国青少年的近视现状。在1888年，日本政府就制定了学生视力检查的训令，由此日本青少年视力防控拉开了帷幕。......
2023-08-09
-
青少年视力防治实践与创新效果分析及影响因素详细阅读
本研究首次采用LTA模型评估了青少年视力防治干预效果的动态演变阶段特征，并分析影响各阶段干预效果转换的因素。LTA模型可以从多个方面评估两个时间点的行为，阐明个人的行为状态随时间的变化。LTA模型也可以应用于识别和描述具有明显特征的潜在类别个体的特征。......
2023-08-09
-
缓解视疲劳效果评估：青少年视力不良防治实践与详细阅读
干预后，合计在校每天做眼保健操情况每天做组构成比为最高，构成比为44.84%，有时做组构成比仅次于每天做组，干预后构成比为37.56%，从不做组构成比最低，为17.60%。干预后男性和女性每天做眼保健操情况均呈频率上升趋势。从不同居住地角度分析可知，各居住地组干预前在校每天做眼保健操情况的构成比均以有时做组最高，分别为44.40%、40.42%、45.37%和43.48%，各居住地组干预后在校每天做眼保健操情况的构成比均以每天做组最高，分别为47.10%、44.22%、42.83%和44.78%。......
2023-08-09
-
用眼习惯改变-青少年视力不良防治的实践与创新详细阅读
从不同年龄组角度分析可知，各年龄组认为教室里的光线正合适的构成比最高，分别为52.70%、50.76%、45.03%、45.85%、45.88%和34.62%。2015年黄陂区不同人口学特征青少年对教室学习光线的认知情况如表3-43所示。进一步对性别、年龄组、教育程度、学校级别、月均收入和居住地等不同人口学特征进......
2023-08-09
-
遗传因素是青少年视力不良的主要影响因素详细阅读
(三) 遗传因素影响遗传是影响视力的主要因素，尤其是在学生阶段，遗传因素的影响更加明显，有研究显示，双亲视力不良的中小学生视力不良发生率明显高于双亲视力正常的中小学生，这说明遗传因素对于学生视力的影响是根本的，而对于遗传因素的影响医学界也做了大量的研究，但至今还缺少有效的防治方法，目前先天性遗传导致的近视只能通过后天进行改善。......
2023-08-09
相关推荐