EFA主要用来初步确定因子个数、指标与因子的关系及因子与因子的关系。探索性因素分析示意图如图5-2所示。从干预效果条目EFA模型拟合指数的结果看，4因子模型的χ2、AIC、BIC和aBIC值均最小，而TLI和CFI值最大。图5-3 探索性因素分析碎石图......
2023-08-09
潜在转换分析与青少年视力不良防治
【摘要】：潜在转换分析是潜在类别分析的扩展，是混合分布模型的一种。潜在类别概率和转移概率的预测可以使用Logistic回归直接并入LTA，如分组变量。LTA是以人群为导向的，个体被分为不同的亚组，是在潜在类别分析基础上的项目反应模式。注：P是转换概率，如P12代表第一个潜在类别在时间t时向在t+1时的第二个潜在类别转换的概率。LTA模型是横断面潜在类别分析的纵向应用。
潜在转换分析是潜在类别分析(latent class analysis，LCA)的扩展，是混合分布模型的一种。LTA假定存在未观察到的(潜在的)分类变量(类别)用来解释观察到的变量之间的关联。它估计三组参数：①转换概率：描述潜在类别从t时间点随时间的变化转到t+1时间点时，各潜在类别之间转换的概率。②描述条件概率：确定研究对象在不同时间点属于不同类别时的概率。③项目反映概率：类似因子分析中的因子负荷。潜在类别概率和转移概率的预测可以使用Logistic回归直接并入LTA，如分组变量(如性别、种族/民族)。LTA是使用潜在类别分析来了解不同潜在类别人群随时间的变化，包含两个或两个以上的潜在类别变量，允许观测随时间变化在两个分类潜在类别变量的类别间转换，见图5-1。
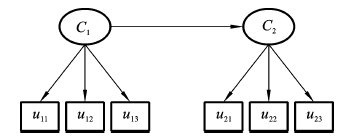
图5-1 LTA示意图
图5-1中，C1为t时间点的潜在类别，C2为t+1时间的潜在类别。
这是一个以人群为导向的分阶段分析方法潜变量的动态变化。LTA是以人群为导向的，个体被分为不同的亚组，是在潜在类别分析基础上的项目反应模式。换言之，它假设不是所有变量之间的关系都是一样的，因此，LTA适合回答哪些类型的人会随时间变化而改变。通过两个不同的时间点，将这些模型合并到单个LTA模型中。LTA可以允许研究者对特定现象进行定性区分，然后将个体归于不同的类别并观察它们随着时间的推移而产生的变化。表5-1比较直观地反映了这种类别随时间变化的关系。
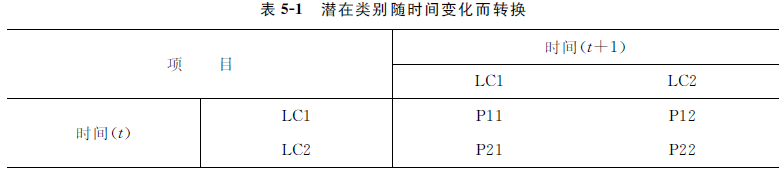
注：P是转换概率，如P12代表第一个潜在类别在时间t时向在t+1时的第二个潜在类别转换的概率。LTA模型也称为隐马尔可夫模型(hidden Markov model，HMM)，它将潜在聚类分析用于重复测量样本，以识别研究对象在不可直接观测状态之间的动态转换过程。LTA是基于马尔可夫模型发展而来的，是阶段性动态的潜变量模型，可研究个体在过去和未来变化的不同方向。因此，LTA可用于回答关于个人的方向改变问题。LTA不要求变量服从正态分布，并且问卷条目不必处于除正常值之外的测量水平。
LTA也可用于分析一系列的纵向数据。LTA运用最多的就是在纵向测量设计中。当描述分类变量随时间变化时，在调查中设计使用LTA是非常有益的，并且当有多个时间节点和/或时间跨度特别大时，使用LTA特别有用。当我们设计因果关系试验(如随机对照试验(RCT))时，LTA同样适用。LTA模型甚至能计算出RCTs的效果(如效应值)。最后，LTA可能在纵向定性研究中也有用，如果目的是理解和量化某种类型的定性变化，可用结构化访谈和共同编码方案来对数据进行分类。LTA也可以应用于识别和描述具有明显特征的潜在类别个体类特征。例如Jackson，et al模拟了24~32岁的个体之间的酒精依赖的潜在转换模型，描述了三个严重程度不同的状态：无酒精依赖性、轻度酒精依赖性和严重酒精依赖性。随着时间变化，虽然相当大比例的人群在这段时间内酒精依赖性会发生转变，但边际概率在很大程度上是稳定的。
LTA模型需要大样本量的数据，因为小样本或分布不均匀的样本会导致结果的不稳定。换言之，当样本量接近于0的时候，不可能可靠地估计标准误差。当样本量很少时，这时一个或多个亚组很小，某一个潜在类别的概率很低或某一个潜在类别的概率基本为0。因此，LTA的样本量至少要大于100，如果运行混合模型的话样本需要量更大。
虽然使用LTA模型同其他模型一样要求严格(例如在回归分析时要求数据是多变量的正态数据)，并且当用这些假设时是不需要调整(例如分类数据使用Logistic回归而不是普通最小二乘回归法)，但是使用LTA模型需要一个非常重要的假设：局部独立。这意味着潜在一个潜类别中的观察变量应该完全独立于另一个观察变量，但是这并不意味着数据集中的所有观察变量彼此独立。LTA模型是横断面潜在类别分析的纵向应用。LCA模型是基于来自单一群体变量的相似反映来识别独特的亚组或剖面的统计模型。
选择LTA模型作为分析方法来描述本研究，目的是了解干预对象的潜在类别在干预前和干预后(一年以后)的分布概率及随干预时间的变化各潜在类别之间转换的概率变化。本研究假设青少年视力防治干预效果可分为几个阶段S=S1，S2，…，Sn，这些阶段无法直接观测到，但是可以通过两个可观测的维度体现，即用眼习惯改变和用眼行为改变。青少年视力防治干预效果由模型根据这两个维度中k个可观测因素O=O1，O2，…，Ok的表现来测算，每个阶段都对应着各因素不同的概率分布，处于阶段i中各因素变量的概率分布为Bi(i=1，2，…，n)。各变量之间保持其局部独立性，在各阶段中不同的因素之间相互独立。青少年视力防治干预效果的演变过程遵循以下方程：
p(St|S1，S2，…，St-1)=p(St|St-1)
转移矩阵A为转换概率aij=p(St+1=Sj|St=Si)，1≤i，j≤n。青少年视力防治干预效果是动态的目标过程，即使个体在某个时期已经达到较好的干预效果，如果不继续接受干预并不努力维持或者没有保持良好的用眼行为，那么仍有可能在之后的干预中落后，使干预效果变差。
有关青少年视力不良防治的实践与创新的文章
- 详细阅读
-
青少年视力不良防治的实践与创新成果详细阅读
(二) 德国德国作为医疗大国，青少年近视率不足15%。该协会经常深入学校，对幼儿园、中小学的学生进行视力跟踪调查，定期检查学生视力，建立青少年视力档案，发现视力降低者及时进行检查、矫正。并且每年推出青少年视力报告，全面评估德国青少年的近视现状。在1888年，日本政府就制定了学生视力检查的训令，由此日本青少年视力防控拉开了帷幕。......
2023-08-09
-
青少年视力不良防治实践: 抽样街道及学校情况详细阅读
(一) 抽样街道及学校情况1. 抽样街道结果通过采用Excel随机数字法，在每个分区中随机抽取1个街道。具体抽样时，考虑到着重观察小学年龄阶段的效果，因而小学生与中学生的抽样比例设定为2∶1。......
2023-08-09
-
缓解视疲劳效果评估：青少年视力不良防治实践与详细阅读
干预后，合计在校每天做眼保健操情况每天做组构成比为最高，构成比为44.84%，有时做组构成比仅次于每天做组，干预后构成比为37.56%，从不做组构成比最低，为17.60%。干预后男性和女性每天做眼保健操情况均呈频率上升趋势。从不同居住地角度分析可知，各居住地组干预前在校每天做眼保健操情况的构成比均以有时做组最高，分别为44.40%、40.42%、45.37%和43.48%，各居住地组干预后在校每天做眼保健操情况的构成比均以每天做组最高，分别为47.10%、44.22%、42.83%和44.78%。......
2023-08-09
-
用眼习惯改变-青少年视力不良防治的实践与创新详细阅读
从不同年龄组角度分析可知，各年龄组认为教室里的光线正合适的构成比最高，分别为52.70%、50.76%、45.03%、45.85%、45.88%和34.62%。2015年黄陂区不同人口学特征青少年对教室学习光线的认知情况如表3-43所示。进一步对性别、年龄组、教育程度、学校级别、月均收入和居住地等不同人口学特征进......
2023-08-09
-
青少年视力不良防治的实践与创新，数据揭示高发详细阅读
视力不良是损害青少年视力的重要眼病之一，在中小学学生中具有极高的发病率，世界卫生组织也早已将缓解、消除五大类眼病列入“视觉 2020”行动中。而中国青少年视力不良的发病率更是稳居世界第一，据国家卫生部、教育部联合调查，小学生近视的比例约为34%，初中生约为60%，高中生为80%左右，在校大学生近视率更是高得惊人。......
2023-08-09
-
青少年视力不良防治：眼保健操的重要措施和效果详细阅读
近年来，眼保健操逐步完善并简化，成为中小学预防近视的重要措施。经常做眼保健操，可以控制近视眼的新发病例，起到保护视力、防止近视的作用。视力为1.2~1.5的学生应作为重点预防对象，加强用眼卫生知识宣传力度，纠正学生不良用眼习惯，坚持做眼保健操。......
2023-08-09
-
青少年视力防治实践与创新效果分析及影响因素详细阅读
本研究首次采用LTA模型评估了青少年视力防治干预效果的动态演变阶段特征，并分析影响各阶段干预效果转换的因素。LTA模型可以从多个方面评估两个时间点的行为，阐明个人的行为状态随时间的变化。LTA模型也可以应用于识别和描述具有明显特征的潜在类别个体的特征。......
2023-08-09
相关推荐