液体滴在固体表面最后达到平衡的情况如图1-10所示。若σ气-固＞σ液-固，则cosθ为正值，θ＜90°；反之，则90°＜θ＜180°。当θ＜90°时，该液体能润湿固体，如水和玻璃；而90°＜θ＜180°时，该液体则不能润湿固体，如汞在玻璃上就是这种情况。图1-11a表示液体在平面上的两种情况，图1-11b表示液体在管中的两种情况。若凝聚功的一半小于粘着功，则θ＜90°，液体就能润湿固体；反之，则不会发生润湿现象。......
2023-06-26
液体中的密度和压力涨落现象及其对熵增定律的影响
【摘要】：与此相似，尽管不那么明显，液体中也同样发生密度涨落和压力涨落。当液体越来越接近沸点时，密度涨落也越来越明显，以致液体呈乳白色。我们不禁要问，对于这种涨落占主导地位的小物体，熵增定律还起不起作用？不过，我们应该看到，这时熵增定律已经失去了它本来的意义，而不应该认为这个定律不正确。[15]1微米等于0.000 1厘米，“微”常用希腊字母μ表示。
通过前文的讨论，我们明确地知道，熵增定律及其一切推论是完全建立在以数量极大的分子为对象的基础上的，只有这样，所有基于概率的推测，才能变为几乎绝对肯定的事实。如果物质的数量极少，这类推测就不那么可信了。
举例来说，如果把前面例子中那个充满空气的大房间，换成边长各为百分之一微米[15]的立方体空间，情况就完全不同了。实际上，由于这个立方体的体积是10-18立方厘米，只包含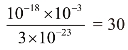
个分子，它们全部集中在一半空间内的概率为
同时，由于这个分子的体积很小，分子改变混合状态的次数达到每秒钟5×1010次（速度为0.5千米/秒，距离只有10-6厘米）以致每秒钟都有一次空出一半空间的机会。在这个房间里，分子在某一端比在另一端更集中些的情况就更可能经常发生了。例如，20个分子在一端，10个分子在另外一端（即有一端多出10个分子）的情况，就会以
即以每秒钟五千万次的频率发生[16]。
因此，在小范围内，空气分子的分布永远是不均匀的。如果能够把分子放得足够大，我们将会看到，分子不断地在某个地方较为集中，然后又散开，接着又在其他地方发生某种程度的集中。这种效应被称为密度涨落，它在许多物理现象中起着重要作用。例如，当太阳穿过地球大气时，大气的这种不均匀性就造成了太阳光谱中蓝色光的散射，因而使天空有了我们所熟悉的颜色，同时使太阳的颜色比实际更红一些。这种变红的效应在日落时尤为显著，因为这时太阳穿过的大气层最厚。如果不存在密度变化，天空就永远是黑色的，我们在白天里也能见到星辰。
与此相似，尽管不那么明显，液体中也同样发生密度涨落和压力涨落。因此布朗运动又有了新的解释，即悬浮在水中的微粒之所以被推来推去，是由于微粒在各个方面所受到的压力在迅速变化的缘故。当液体越来越接近沸点时，密度涨落也越来越明显，以致液体呈乳白色。
我们不禁要问，对于这种涨落占主导地位的小物体，熵增定律还起不起作用？一个细菌，一生都被分子冲来撞去，它当然会对我们关于热能不能变成机械运动的观点嗤之以鼻！不过，我们应该看到，这时熵增定律已经失去了它本来的意义，而不应该认为这个定律不正确。事实上，这个定律的叙述为：分子运动不能完全转变为包含极大量分子的物体的运动。而一个细菌，它比周围分子也大不了多少，对它来说，热运动和机械运动的区别已不存在，它被周围的分子冲来撞去，就像一个人在激动的人群中被大家撞得东倒西歪一样。如果我们是细菌，那么只要我们自己接到一个飞轮上，就会造出一台第二类永动机。但我们已经没有大脑来想办法利用它了，因此，我们无须因我们不是细菌而感到遗憾。
当把熵增定律应用到生物体上时，仿佛产生了矛盾。实际上，生长着的植物（从空气中）摄入简单分子二氧化碳，（从土壤里）吸收水分，并把它们合成复杂的有机物分子以组成自身。从简单分子到复杂分子意味着熵的减小。事实上，在其他情况下，如燃烧木头而把木头分子分解成二氧化碳和水分子时，这个过程是熵增大的过程。难道植物真的违反了熵增定律了吗？是不是植物内部真的像过去的一些哲学家认为的那样，有种神秘的活力在帮助它生长呢？
对这个问题的分析表明，并不存在这种矛盾，因为植物在摄入了二氧化碳、水分和某些盐的同时，还吸收了许多阳光。阳光中除了有能量——它被植物储存在体内，将来又在植物燃烧的时候释放出去——之外，还有所谓的“负熵”（低熵），当植物的绿叶将光线吸收进去，负熵就消失了。因此，在植物叶子中进行的光合作用包含以下两个过程：①太阳的光能转变为复杂有机物分子的化学能；②太阳光的低熵降低了植物的熵，使简单分子构筑成复杂分子。用“有序对无序”的术语来说就是：太阳的光线被绿叶吸收时，它的内部秩序也被剥夺走，并传给分子，使它们能够构成更复杂和更有秩序的分子。植物从无机界得到物质供应，从阳光中得到负熵；而动物靠吃植物（或其他动物）来得到负熵，因而可以说是负熵的间接使用者。
【注释】
[1]马克·吐温是著名的美国作家。在他的《漫游外国记》中有这样一则幽默故事：几个去阿尔卑斯山远足的人，想测量山的高度。这本来可以由气压计的读数计算出来，也可以通过测量水的沸点计算出来，但他们却记成把气压计放在水中煮一下，结果导致气压计损坏，而煮过气压计的水用来做汤时，味道竟然很好。
[2]这里的数据均是在标准大气压下测得的。
[3]红巨星：见第十一章。
[4]1码=0.9144米。
[5]欧美人有饮茶加糖的习惯。
[6]当金属丝处于高温状态时，它内部电子的热运动将变得足够猛烈，使得一些电子从表面射出。这种现象已被应用于电子管，是无线电爱好者所熟知的事实。
[7]此处省去了52张牌以外的、可代替任意一张牌的“百搭”所引起的复杂变化。
[8]实际上概率还要小一些，因为上述计算中还包括“四头一只”（暂且这样称呼四张同点牌加上其他任意一张的情形）。这种概率为
[9]半径为1的圆，周长为半径的2π倍，即2π。因为四分之一弧长为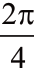
，就是
。
[10]由于气体分子间的距离很大，空间并不拥挤，所以在一定体积内虽已有一大堆分子，却并不影响其他分子的进入。
[11]一间10英尺宽、15英尺长、9英尺高的房间，体积为1 350立方英尺，或5×107厘米3，可容纳5×104克空气。空气分子的平均质量为30×1.66×10-24=5×10-23克，所以总分子数为5×104/5×10-23=1027。
[12]必须考虑到，由于动量守恒定律排除了所有分子向同一方向运动的可能性，因此水分子一定是以一半对一半的速度分布。
[13]还有所谓的“第一类永动机”，即不用提供能量而能自行做功的机械装置，这是违背能量守恒定律的。
[14]1磅=0.453 59千克。
[15]1微米等于0.000 1厘米，“微”常用希腊字母μ表示。
[16]严格地说，这是起码有10个分子聚在半边的概率，而不是刚好有10个分子在一端，另外10个在另一端的概率。
有关从一到无穷大 科学中的事实与猜想的文章
- 详细阅读
-
熵增定律：从无序到有序，真正的蒸汽机如何转化详细阅读
熵增定律也可被称为无序加剧定律，在上述的所有例子中，当熵达到最大值时，分子的位置和速度都是完全无规则地分布着，任何使它们的运动有序化的做法都会引起熵的减小。那么，真正的蒸汽机是怎样在不违反熵增定律的前提下把热能变为机械能的呢？熵增定律说明，系统的总熵要增大，因此只要第二个因素比第一个大一些就行。......
2023-08-05
-
情绪压力对身体的影响详细阅读
身体的情绪地图家人都知道我有个小小的习惯——喜欢洗头发。或者，用另一个说法来解释，就是身体提供了心理问题一个“宣泄”的窗口。因此，根据世界心理卫生组织的统计，大约有70%以上有心理障碍的人会以“攻击”身体器官的方式来消化自己的情绪困扰。由此可知，除了环境污染、饮食内容、卫生习惯等等为人熟知的因素之外，情绪压力绝对在其中扮演了举足轻重的角色。......
2024-07-17
-
侧压力系数及其对挤压性围岩隧道的影响详细阅读
由图可见，当k小于1时，随着侧压力系数的增加，拱顶沉降先减小，当k大于1时近似线性增大。而水平收敛则随侧压力系数的增加而近似以指数形式增加。随着侧压力系数k的增大，塑形屈服由节理面屈服主导向岩体剪切破坏转化。图3.5不同侧压力系数时围岩塑性区分布......
2023-09-21
-
工作压力对生理、心理和行为的影响及其损害详细阅读
但是，由于压力影响生产力和组织效率，我们对工作压力的关心主要集中于其不良影响。（一）压力对生理、心理和行为的影响压力主要在生理的、心理的和行为的三个领域中发生影响。过劳死的发生是由于长时间工作导致的不健康生活方式所致，比如吸烟、不良饮食习惯、缺乏锻炼、失眠，这些引起了体重增加，连同有压力的工作环境，损伤了心脏血管系统，导致了中风和心脏病发作。......
2023-08-02
-
黎曼假设对素数密度函数的影响详细阅读
高斯在研究素数密度函数时，以敏锐的观察力捕捉到密度函数与函数有关，当N越大时，近似程度就越高，即.这也给出了一个计算小于数N的素数个数的近似公式：，显然，“～”与“=”之间有一个误差项，一般来说，比真实的π（N）要小，也就是说它给出了一个较低的估计，后来的数学家发现函数t作为π（N）的估值更加准确，这个函数记为t，一般来说Li（x）比π（x）要大，它给出了一个较高的估计，如图9-3（1）所示.当然......
2023-11-19
- 详细阅读
-
电子风力对电迁移现象的影响详细阅读
是假想电荷数，它所表示的是电子与扩散原子之间动量交换的力的等效效果；eE是电子风力，在良导体中通常它是直接力的十倍左右，在金属的电迁移现象中电子风力的作用要远大于直接力。所以，在电迁移现象中，被增强的原子扩散通量方向通常与电子漂移通量方向一致。换句话说，它将会体验到更大的电子散射作用，以及更大的电子风产生的力的作用，从而将其推向下一个平衡位置，即该原子扩散前空位所在位置。......
2023-06-20
相关推荐