熵增定律：从无序到有序，真正的蒸汽机如何转化能量？

2023-08-05 理论教育版权反馈

【摘要】：熵增定律也可被称为无序加剧定律，在上述的所有例子中，当熵达到最大值时，分子的位置和速度都是完全无规则地分布着，任何使它们的运动有序化的做法都会引起熵的减小。那么，真正的蒸汽机是怎样在不违反熵增定律的前提下把热能变为机械能的呢？熵增定律说明，系统的总熵要增大，因此只要第二个因素比第一个大一些就行。

从前文完全取自日常生活的计算概率的例子里，我们知道对象的数量很少时，概率计算往往是不怎么合适的，而当数目增多时，就会越来越准。这就使得概率定律在描述有多得数不清的分子或原子组成的物体时，就特别有用了，即使是非常小的物质我们也能用概率定律方便地处理它。因此，对于六七个醉汉，每个人各走二三十步的情况，统计规律只能给出大概结果，而对于每秒钟都经历几十亿次碰撞的几十亿个染料分子来说，统计定律导出了极为严格的扩散定律。我们可以这样说，试管中那些原来溶解在一半水中的染料，将在扩散过程中均匀地分布在整个液体中，因为这种均匀分布比原来的分布具有更大的可能性。

同样的道理，在你坐着看这本书的房间里，四堵墙内、天花板下、地板之上的整个空间均匀地充满着空气，从来没有发生过这些空气突然自行聚集在某个角落，使你在椅子上窒息的情况。不过，这种令人恐怖的事情并不是绝对不可能的，它只是极不可能发生而已。

为了弄清这一点，我们假设有一个房间，被一个想象的平面平均分成两个部分，这时，我们考虑一下这两个部分的空气分子最有可能表现出怎样的分布呢？当然，这个问题和前文讨论过的投掷硬币的问题一样。任选一个单独的分子，它位于房间里左半部分或者右半部分的概率相等，正如投掷一枚硬币时，正面朝上和反面朝上的概率相等。

第二个、第三个，以及其他所有分子在不考虑彼此作用力的情况下^[10]，在房间左半部分和右半部分的机会是相等的。分子在房间两半部分的分布，正如一大堆硬币的正反分布一样，一半对一半的分布是最有可能的，在图84中我们已经看到了这一点。我们还看到，投掷的次数越多（或分子的数目越大），50%可能性就越来越确定；当数目更大时，这种可能性就会变为现实。在一间标准大小的房子里，约有1027个分子^[11]，它们同时聚在右半间（或左半间）的概率为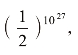： pagenumber_ebook=222,pagenumber_book=218 即1比

另一方面，空气分子以0.5千米/秒左右的速度运动，因此，从房间的一端跑到另一端只需要0.01秒，在1秒内，房间内的分子就会进行100次重新分布。于是，要等到所有分子都处于右边（或左边）房间需要10299999999999999999999999998秒，而宇宙的年龄只有1017秒！所以，你可以继续安静地读书而不必担心会发生突然窒息的灾难。

再举个例子，我们考虑在桌子上放一杯水。我们知道由于水分子无规则的运动，它们以很高的速度向各个方向运动，但是由于分子间的作用力使它们不致溢出。

既然每个分子单独运动的方向完全受概率定律的支配，我们就应该考虑到这样一种可能性：在某个时刻，杯子上半部分的所有分子都具有向上的速度，这时下半部分的水分子都具有向下的速度^[12]。此时，在两组水分子的分界面处，内聚力是沿水平方向的，因此不能阻挡这种分离的愿望，这时，我们将看到一个非同寻常的物理现象：上半杯水以子弹的速度自动飞向天花板。

还有一种可能是水分子的全部热能偶然地集中在这杯水的上层，因而上面的水猛烈地沸腾，下面却结成了冰。你为什么从没有见过这种事情发生？不是因为它绝不可能发生，而是极不可能发生。实际上，如果你尝试计算无规则运动的分子偶然获得的相反的两组速度的概率，就会得到一个与全部空气分子聚集在房间某个角落的概率相近的比较小的数值。同样，由于分子碰撞，一部分分子失去大部分动能，同时另外一部分分子得到这部分能量的概率也是小到可以忽略的。因此。我们实际看到的情况的速度分布，正是具有最大概率的分布。

如果某个物理过程开始的时候，其分子的位置和速度未处于最可能的状态，例如从房间的某个角落释放出一些空气，或者在冷水上面加一些热水，这时会发生一系列的物理过程使系统从较不可能的状态转化为最可能的状态。气体会均匀地扩散到整个房间，上层热水的能量会向下层的冷水传递，直到全部的水达到相同的温度。因此，我们可以这样说：一切依赖于分子无规则热运动的物理过程都朝着概率增大的方向发展，而过程停止时，即达到平衡状态时，也就达到了最大概率。在房间内空气分布的那个例子中，我们已经看到，分子各种分布的概率往往是一些很不方便的小数字（如空气聚集在半间屋子里的概率为　通常我们都取各种概率的对数。这个数值被称为熵，它在有关物质无规则热运动的问题中扮演重要的角色。现在，可将前面那些有关物理过程中概率变化的叙述修改如下：一个物理系统中的任何自发变化，都朝着熵增加的方向发展，而最终达到平衡状态时，则对应熵的最大可能值。

这就是著名的熵增定律，也被称为热力学第二定律（第一定律为能量守恒定律）。正如你所看到的，这里面并没有令人害怕的东西。

熵增定律也可被称为无序加剧定律，在上述的所有例子中，当熵达到最大值时，分子的位置和速度都是完全无规则地分布着，任何使它们的运动有序化的做法都会引起熵的减小。熵增定律的另一个比较实用的数学公式可以从热能转化为机械能的问题中推导出来。大家知道，热能就是分子的无规则运动，因此不难理解，把物体的热能全部转化为宏观的机械运动就是强迫物体的分子都向一个方向运动。我们已经看到，一杯水中有一半自行冲向天花板的可能性太微乎其微了，实际上不可能会发生。因此，虽然机械能可以全部转化为热能（例如通过摩擦），但热能却永远不能全部转化为机械能。这就排除了所谓的“第二类永动机”——它在室温下吸收物体的热量、降低物体的温度来获得能量来做功——存在的可能^[13]。例如，不可能设计出这样一艘船，它产生的蒸汽不用烧煤，只靠吸收被吸进舱室的海水的热量，并把变为冰块的海水扔回海里来完成。

那么，真正的蒸汽机是怎样在不违反熵增定律的前提下把热能变为机械能的呢？它之所以能做到这两点，是由于在燃料燃烧所释放的热能中，只有小部分转化为机械能，其他大部分热量有的由废气带出，有的被专门的冷却设备吸收。这时，整个系统有两种不同的熵变过程：（1）随着一部分热能转变为活塞的机械能，这时熵会减小；（2）随着其余热量从锅炉进入冷却设备，这时熵会增大。熵增定律说明，系统的总熵要增大，因此只要第二个因素比第一个大一些就行。我们可以这样来更好地说明这种情况：在六英尺高的架子上，放着一个5磅^[14]的重物。根据能量守恒定律，这个重物不可能在没有外力的情况下飞向天花板，然而，它却能向地板上甩下它自身的一部分，并用这时释放的能量使其余部分上升。

用同样的方法，我们可以使一个系统中的某一部分的熵减小，只要使其他部分的熵增大来补偿它就行了。换句话说，对于一些进行无序运动的分子，如果我们不在乎其中一部分变得无序的话，是可以使另外一部分变得有序一些的。的确，在许多实际的情形中，如对所有的热机械来说，我们正是这样做的。

熵增定律：从无序到有序，真正的蒸汽机如何转化能量？

相关推荐