拓扑学中的数学定理：多面体的顶点数、棱数和面数的关系

2023-08-05 理论教育版权反馈

【摘要】：几何学中关于这一内容的分支称为拓扑学[2]。两种几何学的不同之处就在于此。表2各种多面体的顶点数、棱数和面数前三行的数据，乍一看貌似没有太大联系。由此可以看出，V+F=E+2是在拓扑学里被广泛应用的一个数学定理，因为这个关系式只涉及几个几何学单位的数目，并不涉及棱的长短或面的大小等量度。看一下图16就一目了然了，和图14一样，有两种不同的几何体，全部是多面体。如此一来，V+F=32，而E+2=34，不相等了。

在学校，你应该对几何学比较熟悉，它是一门关于空间量度的科学^[1]，在你的记忆中，它的主要内容是一大堆讲述长度和角度等数值关系的各种定理（比如，讲直角三角形三边长度关系的毕达哥拉斯定理）。但是，长度和角度并不是空间的基本性质之一。几何学中关于这一内容的分支称为拓扑学^[2]。

我们用一个典型的例子来解释一下拓扑学。想象一个球面，它作为一个封闭的几何面，可以用一些线把它分成很多区域。我们不妨这么操作：在球面上随意选择一些点，用不相连的线将它们连接起来。这样一来，连线的数目、这些点的数目和区域的数目之间的关系是怎样的呢？

特别显而易见的一点：要是将这个圆球挤压成像南瓜一样的扁球，或者拉成像黄瓜一样的长条，这样一来，点、线、面的数目和圆球时的数目明显还是一样的。实际上，就像随便拉挤压扭一个气球时所能获得的那些曲面（不过不要把气球弄破）一样，我们能够得到任意形状的闭曲面。在这种情况下，丝毫的改变都不会出现在上面问题的提法和结论中。但是在一般几何学中，要是把一个正方体变成平行六面体，或者把一个球体压成饼状，各种数值（例如线的长度、面积、体积等）就会发生很大变化。两种几何学的不同之处就在于此。

现在，我们把这个划分好的球面的每一区域展开，如此一来，球体就变成了多面体（图13），相近区域的界限变为棱，之前挑选的点变为顶点。

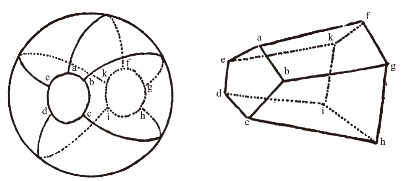
pagenumber_ebook=47,pagenumber_book=43

图13　一个划分成若干区域的球面变成一个多面体

如此一来，我们之前那个问题就变为（实质上丝毫没有改变）：一个任意形状的多面体的面、棱与顶点的数目之间的关系是怎样的呢？

图14所示为5种正多面体（也就是每个面都有同样多的棱和顶点）和一个随便画出的不规则多面体。

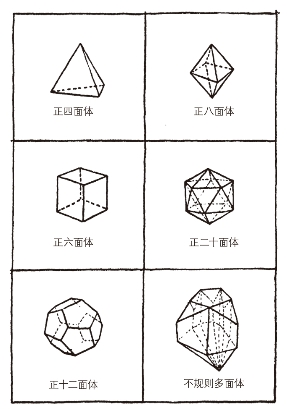
pagenumber_ebook=48,pagenumber_book=44

图14　5种正多面体（有且仅有5种）和一个不规则多面体

我们来数一下每一种多面体几何所拥有的顶点数、棱数和面数，看看它们各自有着怎么样的关系。

数完之后，我们得到表2。

表2　各种多面体的顶点数、棱数和面数

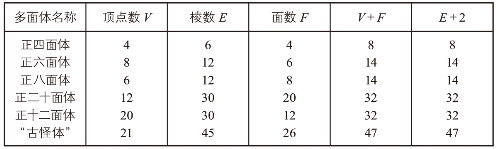
pagenumber_ebook=48,pagenumber_book=44

前三行的数据，乍一看貌似没有太大联系。不过认真观察就会发现，顶点数和面数加起来永远比棱数大2。所以，我们由此写出这样一个关系式：

V+F=E+2

这关系式是适用于图14中这几个特殊的多面体呢，还是适用于所有的多面体呢？你可以再画几个其他形状的多面体，数一下它们的顶点数、棱数和面数。你就会发现，结果依然是一样的。由此可以看出，V+F=E+2是在拓扑学里被广泛应用的一个数学定理，因为这个关系式只涉及几个几何学单位（顶点、棱、面）的数目，并不涉及棱的长短或面的大小等量度。

17世纪法国的大数学家笛卡儿最开始注意到这个关系，另一位数学大师欧拉对其给出了严格证明。这一定理现在被称为欧拉定理。

下面引用一下古朗特和罗宾斯的著作《数学是什么？》^[3]中欧拉定理的证明过程。我们不妨看看，这一类型的定理是怎样证明的。

我们可以把给定的简单多面体设想成用橡皮薄膜做成的中空体［图15（a）］，这样做的目的是证明欧拉公式。假如我们削去它的一个面，接着让它变形，把它摊成一个平面［图15（b）］。的确，如此一来，面和棱间的角度都会变化。但是，这个平面网络的顶点数和边数都与之前的多面体一样，原来多面体的面比多边形的面多了一个。接下来我们准备证明，对于这个平面网络有V-E+F=1。如此，再加上那个被削去的面，结果就成了：对于原多面体，V-E+F=2。

我们把这个平面网络“三角形化”，也就是为网络中不是三角形的多边形加上对角线。如此一来，E和F均会增大，但V-E+F仍然保持不变，因为每加一条对角线，E和F都增加1。如此添加下去，最终全部的多边形都会变为三角形［图15（c）］。因为添加对角线并不会改变这个数值，在这个三角形化的网络中，V-E+F依然和三角形化之前的数值一样。

网络边缘也有一些三角形，其中有一些（如△ABC）仅有一条边位于边缘，有的也许有两条边位于边缘。我们拿掉这些边缘三角形上不与其他三角形共有的部分［图15（d）］，即从△ABC上拿掉边AC和这个三角形的面，只留下顶点A、B、C和两条边AB、BC；从△DEF上拿掉这个三角形的面、两条边DF、FE和顶点F。

pagenumber_ebook=50,pagenumber_book=46

图15　欧拉定理的证明（图中所示的是正方体的情况，但所得到的结果对任意多面体来说都是成立的）

在拿掉△ABC的边和面之后，E和F各减小1，但V不变，所以V-E+F不变。在拿掉△DEF的点、边和面之后，V减小1，E减小2，F减小1，所以V-E+F依然不变。以合适的方式渐渐减少这些边缘三角形，到最后只剩下一个三角形。一个三角形有三条边、三个顶点和一个面。对于这个简单的网络V-E+F=3-3+1=1。我们已经知道，V-E+F的值并不会随着三角形的减少而发生变化，因此，在开始的那个网络中，V-E+F也应该等于1。不过，原来那个多面体又比这个网络多一个面，所以，对于完整的多面体，V-E+F=2。欧拉定理就这样被证明了。

有且仅有5种正多面体存在（即图14中那5种），这就是欧拉公式的一条有趣的推论。

仔细推敲一下前几页的讨论，你可能会看到，我们在画出图14所示的“各种不同”的多面体以及在用数学推理证明欧拉定理时都作出了一个内在的假设，这在很大程度上限制了我们对多面体的选择。多面体必须没有任何透眼，这就是那个内在假设。这里所说的透眼，就像甜甜圈或橡胶轮胎中间的那个窟窿一样，而不是像气球表面被撕掉一块后的形状。

看一下图16就一目了然了，和图14一样，有两种不同的几何体，全部是多面体。

我们现在来观察一下，这两个新的多面体是否适用欧拉定理。

在第一个几何体上，我们能数出16个顶点、32条棱和16个面。如此一来，V+F=32，而E+2=34，不相等了。在第二个几何体上，我们能数出28个顶点、60条棱和30个面，即V+F=58，而E+2=62，这样就差得更多了。

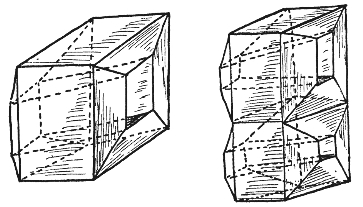
pagenumber_ebook=52,pagenumber_book=48

图16　两个有透眼的多面体（它们分别有一个和两个透眼。这两个多面体的各个面不都是矩形，但我们知道，这在拓扑学中是无关紧要的）

怎么会出现这种情况呢？这两个例子无法用于欧拉定理的证明和推导，那它们错在哪里了呢？

错误在于：我们可以把之前想到的多面体作为一个气球或球胆，而把目前这种新型多面体作为橡胶轮胎或者其他较为复杂的橡胶制品。对于这种多面体，上面证明过程中的必要步骤“割去它的一个面，让它变形，使它成为一个平面”是无法实现的。

如果只是用剪刀剪去球胆的一块表皮，这个必要步骤依然可以实现。但对一个轮胎而言，怎么也无法实现。如果图16还无法让你相信这一点，那么你可以找一条旧轮胎自己动手试试。

然而，对于这种比较复杂的多面体，V、E和F之间还是有一定关系的，只不过不是之前的那种关系罢了。对于甜甜圈形的多面体（也就是环状圆纹曲面形的多面体），科学的说法应该是V+F=E。对那种蜜麻花形的多面体，就是V+F=E-2。对于一般的多面体，就是V+F=E+2-2N，N就是透眼的个数。

另一个典型的拓扑学问题和欧拉定理有着密切的关系，它就是我们说的“四色问题”。把一个球面划分为几个区域，在球面上涂色，不能让任意两个相邻的区域颜色一样。想要完成这个工作，至少要几种颜色？两种颜色通常来说是不够用的，这很容易看出来。三条边界汇集于一点时［例如美国的弗吉尼亚、西弗吉尼亚和马里兰三个州的地图，见图17（a）］，就需要三种颜色。

不难找到需要四种颜色的例子，如图17（b）所示（德国吞并奥地利时的瑞士地图）^[4]。

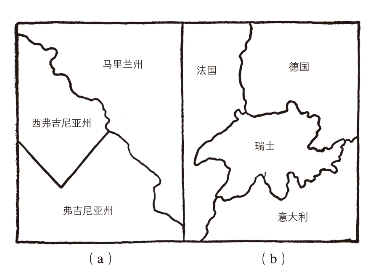
pagenumber_ebook=53,pagenumber_book=49

图17　涂颜色的例子

（a）马里兰州、弗吉尼亚州和西弗吉尼亚州的地图；（b）瑞士、法国、德国、意大利的地图

然而，无论你怎样划分，也无法得到一张必须用四种颜色以上的地图，这在球面上或者在平面上都是一样的^[5]。这样一来，无论是如何复杂的地图，四种颜色就足够让边界两边的区域无法混淆。

但是，假如这种说法没错的话，我们可以从数学上去证实它。可惜的是这一问题经过数代数学家的辛劳奋斗，到现在依然没有成功。这又是一个典型例子，虽然没有人怀疑它的正确性，但也没有人能够给出证明。如今，我们只有从数学上去证明有五种颜色就已经够了。这一证明是通过把欧拉关系式应用于国家数、边界数和几个国家碰到一起的三重、四重等交点数而得出来的。

由于这一证明过程特别复杂，写下来会跑题太多，在这里就不详细叙述了。读者能在不同种类拓扑学的书中找到它，并用它来度过一个愉悦的晚上（也许还会晚上睡不着觉）。要是有人可以证明不用五种而只用四种颜色就可以给所有的地图上色，或者琢磨出一幅四种颜色都不够用的地图，不管哪一个成功了，纯粹数学的年鉴上就会把他的大名印上100年之久。

这个涂色的问题，在球面和平面等简单情形下无论如何也证明不出来，说起来还真好笑；但在复杂的曲面上却得到了比较顺利的证明，比如甜甜圈形和蜜麻花形的曲面。举个例子，对于甜甜圈形的曲面已经得到结论，无论如何分划，要让相近区域的颜色不一样，至少需要七种颜色。这样的例子也已经出现了。

读者可以再动点脑筋，弄来一个充气轮胎，然后找到七种颜色的油漆，再给轮胎上漆，让每种颜色都与其他六种颜色挨着。假如能做到这一点，他就能说自己真正了解甜甜圈形曲面。

拓扑学中的数学定理：多面体的顶点数、棱数和面数的关系

相关推荐