图形认识与测量-小学数学综合实践活动课程设计

2023-08-03 理论教育版权反馈

【摘要】：教师要给学生充分的讨论交流时间，让学生单独回忆的知识由“线性”进一步走向丰富，并有意识地引导学生认识和理解概念之间的联系与区别。）图6-1几种四边形的关系关于圆。

(一)教学内容

人教版数学教材六年级下册第86页的相关内容。

(二)教材分析

人教版整套教材对于空间与图形知识的编排，是按照内容本身的特点和学生的认知规律，以螺旋上升的形式呈现。本节内容是对第一、第二学段图形与几何知识的系统整理，着重复习小学阶段所学习的各图形的特点、关系，以及部分几何图形的周长、面积、体积计算。

例1是对学过的平面图形和立体图形进行分类与整理，教材以两个同学对话的形式呈现教学内容。教师要留给学生充足的回忆时间，要引导学生抓住每种图形的本质属性，并逐级分类整理，让学生的回忆由“点状”，逐步呈现出“线性”，并突出对“分类”“集合”等数学思想的感悟，形成知识网络。

例2是更为细化地对平面图形的知识进行整理和复习。教材用五个问题，从线到面，从直线图形到曲线图形，体现了平面图形由简单到复杂的演变过程，符合学生的认知规律。教师要给学生充分的讨论交流时间，让学生单独回忆的知识由“线性”进一步走向丰富，并有意识地引导学生认识和理解概念之间的联系与区别。

在本课时，教师要重点启发学生理清点、线、面、体之间的联系，找准知识的“生长点”与“延伸点”，沟通知识间的内在联系，形成知识系统，并充分体会“类比”“转化”“数形结合”的数学思想，受到普遍联系、对立统一、直与曲、变与不变等哲学思想的熏陶。

(三)教学目标

（1）通过复习，全面掌握小学阶段所学的几何图形的特征和关系。

（2）从点到线，再到面、体，让学生感受几何图形由简单到复杂的演变过程，在比较的基础上沟通知识间的内在联系，形成知识系统。

（3）充分体会“分类”“集合”“类比”“转化”“数形结合”的数学思想。

（4）在整理复习的过程中，进行相应的普遍联系、对立统一、直与曲、变与不变等哲学思想的熏陶。

(四)教学重点

几何图形的特征和关系，知识系统的建立。

(五)教学难点

数学思想和哲学思想的体会和熏陶。

(六)教学准备

准备课件。

(七)教学过程

1.谈话导入

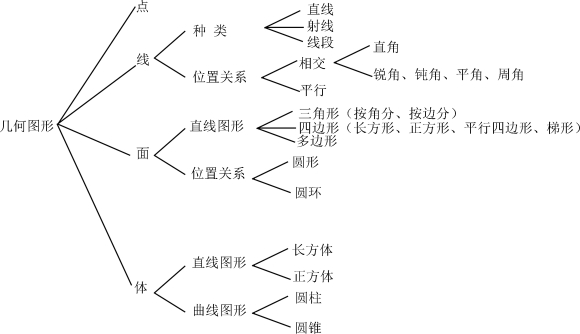
（1）关于几何图形，我们这六年都学过哪些知识?（学生自由回答，教师按点、线、面、体分类板书）。

（2）请大家试着把我们学过的几何图形分类。（板书如下）

pagenumber_ebook=66,pagenumber_book=57

2.探究、讨论、辨析

（1）把小学阶段学过的几何图形归类为点、线、面、体四类，这四类图形有什么关系?（两点定线，线围成面，面围成体，面在体上，化圆为方）。

师：世界上没有孤立存在的事物，所有事物之间都有千丝万缕的联系，我们认识事物时，既要分辨各种事物独有的特征，又要找到事物之间的普遍联系，这样才能让认识更深入、更全面。

（2）回忆讨论直线、射线、线段的联系与区别。

①提示学生从端点数、特点、能否测量这三个方面来思考，并完成表格6-1。

表6-1　直线、射线、线段的特点

pagenumber_ebook=67,pagenumber_book=58

②直线、射线、线段之间有什么联系?

③同一平面内的两条直线有几种位置关系?平行线有什么特点?相交有几种情况?

（3）关于角。

什么是角?角各部分的名称是什么?角与点、线的关系怎样?角的大小与什么有关?如果按角的大小分，角可以分为哪几类?几种角之间有什么关系?

（4）关于三角形。

我们在小学阶段主要是从哪些方面研究三角形的?

①三角形有什么特性?（稳定性）。

②如何给三角形分类（按角分，按边分）?各类三角形之间是什么关系（用集合图表示）?

③三角形的边有什么性质?

④三角形的内角和是多少度?怎么证明?

⑤三角形的周长怎么算?面积呢?（第2课时再展开。）

（5）关于四边形。

①我们学过的四边形有哪几种?它们之间是什么关系?

②试试用集合图表示几种四边形的关系，并说一说（图6-1）。

③平行四边形有什么特征?梯形有什么特性?

④长方形和正方形各有什么特征?

⑤怎样计算长方形、正方形、平行四边形、梯形的周长和面积?（第2课时再展开。）

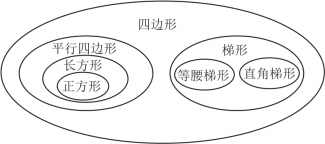
pagenumber_ebook=67,pagenumber_book=58

图6-1　几种四边形的关系

（6）关于圆。

①关于圆，我们学过哪些知识?

②圆与上面的平面图形有什么不同?

③圆与平面图形有什么联系?

④怎样计算圆的周长和面积?（第2课时展开。）

师：圆是曲线图形，我们在计算圆的周长和面积时，化曲为直，说明曲与直看起来是互相矛盾的、对立的，但在一定条件下可以互相转化。世上的事物也一样，在对立中有统一，在追求大同时又要允许有小异。

3.课堂小结

这节课，我们对小学阶段学过的平面图形和立体图形进行了分类和整理，点、线、面、体之间既各有特点又紧密联系，既独立又统一。数与形可以互相表达，曲与直可以相互转化。

(八)教学反思

小学数学中充满着矛盾：如数概念中的正数与负数、奇数与偶数、整数与分数等，数的连接方式如加与减、乘与除等，几何图形中的点与线、直线与曲线、平面与曲面、方体与球体、棱与角等，这些矛盾方既相互对立又相互联系，在一定条件下还相互转化。这一节的教学内容提供了很好的哲学素材，教师有意识地用哲学的显微镜、望远镜去开发和教学，对学生进行哲学的熏陶，让学生学习数学不要只停留在形式逻辑的推理和烦琐的计算中，而要用辩证逻辑的科学方法理解数学的本质和意义，从哲学宝库中寻找开拓思维的新武器，从而使思维空间更宽、更广、更新。

（华南师范大学附属小学　常春丽）

图形认识与测量-小学数学综合实践活动课程设计

相关推荐