Kim等[2]研究发现不同性别、年级、学科和性格的学生在使用不同的平台搜寻信息的频率和使用目的方面有显著差异。Sin[3]研究了性别—年级、问题解决方式等特征对留学生的信息源使用以及日常生活信息搜寻的差异性影响。基于社会化媒体学术信息搜寻行为影响因素调查所收集的273个样本，采用独立样本t检验和单因素方差分析的统计分析方法对分组样本进行比较。......
2023-08-03
结构模型分析结果: 社会化媒体用户学术信息搜寻行为
【摘要】：为了进一步分析造成这一结果的原因，这里将信息有用性作为固定因变量，系统质量作为固定自变量，其他变量单独或两两同时进入回归模型进行分析，结果如表4-7所示，可以看到，当服务质量和信息源可信度同时进入回归模型后，系统质量对信息有用性的影响不再显著，如表4-7中的模型7所示，说明用户在判断社会化媒体中学术信息有用性的时候，系统质量会因为用户重视服务质量和信息源可信度而对用户判断信息有用性不再有明显的影响。
利用偏最小二乘法结构化方程建模方法对结构模型中的研究假设进行检验，同时，采用Bootstrap重抽样方法从数据集中重复抽取样本形成新的数据集进行显著性检验，样本数设置为1000，据此可计算得到t估计值。首先，对主效应模型进行分析，结果如图4-2所示。
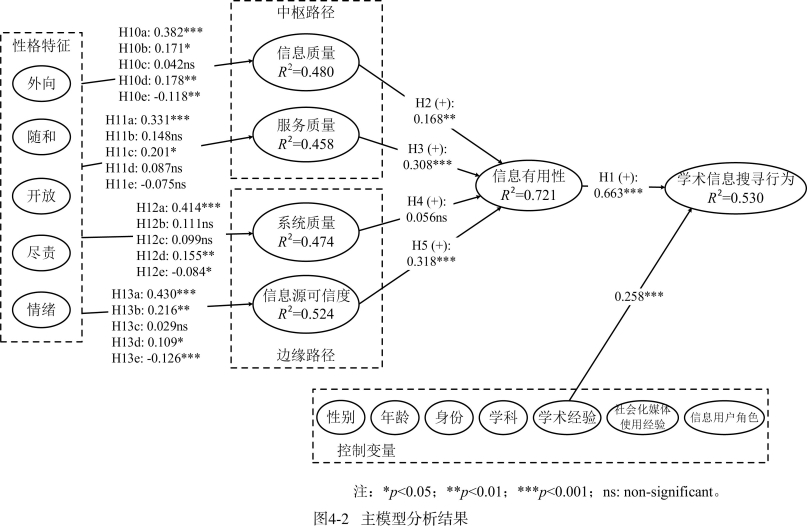
从图4-2可以看到，用户对社会化媒体中学术信息有用性的感知显著地影响用户的学术信息搜寻行为，因此，假设H1成立。从中枢路径和边缘路径对信息有用性的影响来看，属于中枢路径变量的信息质量和服务质量显著地影响用户对社会化媒体中学术信息有用性的感知，因此，假设H2和H3成立；属于边缘路径变量的系统质量对信息有用性不存在显著的影响，因此，假设H4不成立，而信息源可信度显著地影响用户对社会化媒体中学术信息有用性的感知，因此，假设H5成立。从性格特征对中枢路径和边缘路径变量的影响来看，大部分假设成立，具体而言，外向型性格正向显著地影响用户对信息质量、服务质量、系统质量以及信息源可信度的感知，因此，假设H10a、H11a、H12a和H13a成立；随和型性格正向显著地影响用户对信息质量和信息源可信度的感知，因此，假设H10b和H13b成立；开放型性格仅对服务质量存在正向显著的影响，因此，假设H11c成立；尽责型性格正向显著地影响用户对信息质量、系统质量和信息源可信度的感知，因此，假设H10d、H12d和H13d成立；情绪型性格负向显著地影响用户对信息质量、系统质量和信息源可信度的感知，因此，假设H10e、H12e和H13e成立。同时，在主模型中还将性别、年龄、身份、学科、学术经验、社会化媒体使用经验以及信息用户角色作为控制变量指向信息搜寻行为以检验样本特征对信息搜寻行为的影响，从图4-2的结果可以看到，学术经验对信息搜寻行为存在正向的显著性影响，表明用户的学术经验越丰富，他们越可能在社会化媒体中搜寻学术信息以满足自己的信息需求。其他的控制变量对信息搜寻行为不存在显著影响，因此，未将它们的路径系数在图4-2中展示。在主效应模型中，信息搜寻行为的解释方差为0.530，信息有用性的解释方差为0.721，信息质量的解释方差为0.480，服务质量的解释方差为0.458，系统质量的解释方差为0.474，信息源可信度的解释方差为0.524，表明主效应结构模型具有良好的预测效果[63]。
此外，在图4-2的结果中，系统质量对信息有用性不存在显著影响，但从表4-4可以看到，系统质量与信息有用性之间的相关系数为0.739，说明系统质量对信息有用性存在独立的影响作用，它对信息有用性的影响因其他变量的存在而被弱化。为了进一步分析造成这一结果的原因，这里将信息有用性作为固定因变量，系统质量作为固定自变量，其他变量单独或两两同时进入回归模型进行分析，结果如表4-7所示，可以看到，当服务质量和信息源可信度同时进入回归模型后，系统质量对信息有用性的影响不再显著，如表4-7中的模型7所示，说明用户在判断社会化媒体中学术信息有用性的时候，系统质量会因为用户重视服务质量和信息源可信度而对用户判断信息有用性不再有明显的影响。
表4-7 层次回归分析
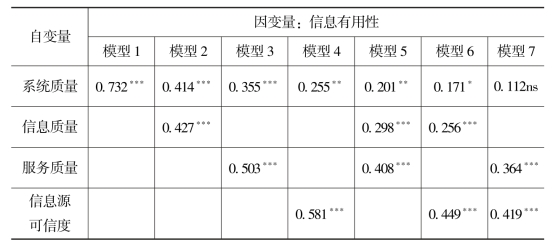
注:*p＜0.05；**p＜0.01；***p＜0.001；ns:non-significant。
主效应模型分析之后，将调节变量加入结构模型中以检验信息需求对中枢路径变量和边缘路径变量与信息有用性之间关系的调节作用。交互效应通过自变量与调节变量之间相乘实现，从表4-8的结果可以看到，与研究假设相反，信息需求对信息质量和服务质量与信息有用性之间的关系存在负向显著的调节作用(模型2和模型3)，因此，假设H6和H7不成立。信息需求对系统质量和信息源可信度与信息有用性之间的关系存在负向显著的调节作用(模型4和模型5)，因此，假设H8和H9成立。在模型2到模型5中，信息有用性的方差解释分别增加了0.020、0.019、0.017和0.017。根据Cohen[64]和Mathieson等[65]对效应量(Effect Sizes)的解释，计算得到模型2、模型3、模型4和模型5的效应量分别为0.074、0.070、0.062和0.062，表示中低水平的效应。总体上看，结构模型具有较好的预测效果。
表4-8 结构模型交互效应结果
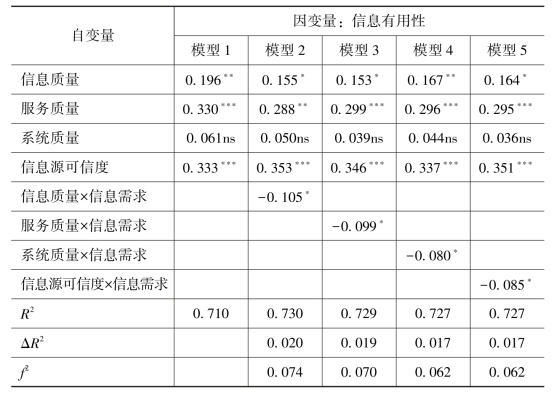
注:*p＜0.05；**p＜0.01；**p＜0.001；ns:non-significant。
f2＝ΔR2/(1-R2)，表示效应大小。[66]效应水平高、中、低的临界值分别是0.35、0.15、0.02。[67]
- 详细阅读
-
社会化媒体用户学术搜寻行为的访谈结果详细阅读
本章通过一对一面谈与一对一在线访谈相结合的方式进行访谈资料收集。其中，时间维度涉及信息获取的时效性和及时性；数量涉及满足信息需求的信息量；任务涉及问题或特定任务驱动的信息需求；内容维度涉及满足信息需求的内容质量、信息类型；对应马斯洛的需求层次，信息需求又可以归纳为生理层面的信息需求、认知层面的信息需求和情感层面的信息需求等。......
2023-08-03
-
研究结果：社会化媒体用户学术信息搜寻行为详细阅读
[75]信息搜寻行为指用户有目的地搜寻信息以实现某项目标，被认为是一个意义建构的过程，个体在这一过程中搜索与其个人观点相匹配的信息，以支持其减少不确定性并作出决策，从而理性地解决问题。Jiang[83]研究基于Web 2.0站点的社会图书馆系统环境下用户的信息搜寻模式，发现大多数用户倾向于合并两种或更多的模式，而每个用户通常有一个占据主导地位的模式。......
2023-08-03
-
社会化媒体用户学术信息搜寻行为研究成果详细阅读
社会化媒体环境下，用户获取和搜寻学术信息等行为受到个性特征、信息源可信度、信息质量、系统质量、服务质量等多种因素的影响。个性特征的差异将用户划分为不同的群体，不同的用户群体在使用社会化媒体参与各种学术信息活动过程中的行为表现会有所不同。......
2023-08-03
-
信息需求调节下社会化媒体用户学术信息搜寻行为详细阅读
近年来，社会化媒体被大众用户广泛地接受和使用，正在不断地渗入人们的日常生活当中，社会化媒体在信息生产、传播与获取过程中扮演着重要角色，逐渐成为主流。各个领域的学者逐渐开始对社会化媒体的相关问题展开研究。学者们认为社会化媒体不仅有助于同行之间的协作与交流，而且便于信息的传播与扩散。大多数研究人员认为社会化媒体工具不仅仅是一种潮流，更代表着学者们交流、合作、获取、共享和传播知识与信息方式的变化。......
2023-08-03
-
社会化媒体用户学术信息搜寻行为调查：数据收集详细阅读
调查问卷采用7点李克特量表进行测量，从1到7表示“强烈不同意”到“强烈同意”。问卷设计完成后展开大范围的调查。大范围的问卷调查共持续四周的时间。本研究的目的之一是分析信息需求在社会化媒体用户学术信息搜寻行为中的调节作用及影响规律，涉及用户搜寻学术信息的相关活动，考虑到高校学生和教师是使用学术信息的主要群体，因此，选取这一群体作为调查对象进行样本数据收集。......
2023-08-03
-
信息需求研究视角：社会化媒体用户学术信息搜寻详细阅读
根据Taylor信息需求模型中信息需求的模糊性和不易表达的特征以及Wilson对信息需求问题的探究，研究人员对信息需求问题的研究重点转向了信息需求发生的情境，这使得用户信息需求产生的情境变得非常重要。从计算机科学视角出发的用户信息需求研究主要关注的是Taylor模型中后两个水平的信息需求，即正式的信息需求和妥协的信息需求，属于可以被具体描述的需求。......
2023-08-03
-
社交媒体用户学术信息搜寻行为研究：研究假设与详细阅读
Cheung等[7]研究网络消费者社区中的在线意见采纳时发现信息有用性显著地影响用户的信息采纳行为。Lin[23]在研究系统特征对虚拟社区成功的影响时发现系统质量影响虚拟社区成员对虚拟社区的满意度。Wang和Lin[26]的研究发现，用户使用博客的意愿会受信息质量、系统质量、博客功能质量等因素的影响。......
2023-08-03
相关推荐