为使er→0，即＜0，最好Vm＞Vl，即虚拟领弹的速度小于从弹速度。所以需设置er=r-rl＞0，即从弹位置较远，需先追赶虚拟领弹，通过合理设计参数kr，飞行中后期进行小范围机动缩小弹目距离偏差，令速度前置角常处于非饱和状态，此时飞行剩余距离较短，协同效果较好。综上所述，虚拟领弹运动参数需满足式中，下标为“0”表示此为初始时刻的值。根据式设计虚拟领弹的初始条件，可使协同策略中的脱靶量较小，时间协同效果较好。......
2025-09-29
多飞行器协同控制：防御弹发射角区域改进
【摘要】：虽然在13.3.1节中得到了防御弹在初始发射角给定情况下的可行攻击角区域，但当防御弹攻击角度给定时，不同的防御弹发射角度将对防御弹飞行弹道产生较大影响，进而对防御弹需用过载以及拦截时间产生影响。图13-4CNGL和TSG时的变化曲线图13-5CNGL和TSG时控制量的变化曲线例13-2本实例给出可得到可行攻击角区域的算例。
虽然在13.3.1节中得到了防御弹在初始发射角给定情况下的可行攻击角区域，但当防御弹攻击角度给定时，不同的防御弹发射角度将对防御弹飞行弹道产生较大影响，进而对防御弹需用过载以及拦截时间产生影响。因此，在防御弹和目标的可用过载约束以及拦截时间约束下，为实现给定的攻击角度，防御弹的发射角也应限定在某一可行区域，本节将给出多约束条件下的防御弹可行发射角区域。
1.可用过载约束下的防御弹可行发射域
当防御弹攻击角度给定时，同样假设防御弹的最大需用过载出现在防御弹发射时刻，联立式（13-32）、式（13-34），并将攻击弹、目标和防御弹的初始状态代入，得到以下不等式：
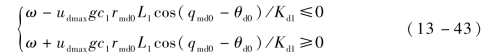
式中，ω=6.388
，其中
分别表示在防御弹初始发射时刻防御弹和攻击弹之间的相对距离以及视线角的一阶导数，其表达式为
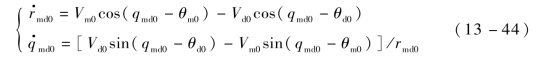
联立式（13-43）、式（13-44）可知，当目标、防御弹和攻击弹的初始位置、初始速度、期望的攻击角度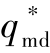
、目标和攻击弹的初始发射角度以及防御弹的安全系数Kd1确定时，求解不等式（13-43）即可得到防御弹可用过载约束下的防御弹可行发射角区域。
同理，在目标可用过载约束下，可得到以下不等式：
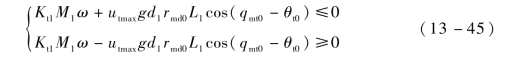
式中，除了防御弹初始发射角θd0未知，其他变量都是已知的。
联立式（13-44）、式（13-45）求解不等式，即可得到目标可用过载约束下的防御弹可行发射角区域。
2.拦截时间约束下的可行发射域
采用与拦截时间约束下的可行攻击角区域求解同样的方法，对拦截时间约束下的防御弹可行发射域进行研究。当期望攻击角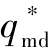
给定时，同样假设tgomd0为θd0的二次函数表达式为
式中，α2，β2，γ2——二次函数系数。
采用拟合的方法得到二次函数表达式系数的步骤如下：
第1步，根据目标和防御弹的可用过载约束，得到可用过载约束下的防御弹发射角区域
。
第2步，在防御弹发射角区域
内选取不同的发射角
（i=1，2，…，m）进行仿真分析，并得到相对应的初始剩余飞行时间估计tgomd0i（i=1，2，…，m）。
第3步，基于仿真得到的不同防御弹初始发射角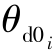
下的tgomd0i数据，拟合得到二次函数系数α2、β2和γ2。
第4步，联立式（13-39）、式（13-40）、式（13-46），可得
求解式（13-47），即可得到防御弹在拦截时间约束下的可行发射域。综合由式（13-43）、式（13-45）、式（13-47）得到的防御弹可行发射域，并求其交集，即可得到满足可用过载约束和拦截时间约束的防御弹可行发射域。
例13-1 目标、攻击弹和防御弹三个飞行器的初始状态及可用过载见表13-1。攻击弹采用导引系数Nm=4的增强比例导引律。仿真步长为0.001 s，当防御弹和攻击弹的距离rmd＜1 m或攻击弹与目标的距离rmt＜1 m时，仿真终止。
表13-1 三个飞行器的初始仿真条件及可用过载
弹道成型制导律（Trajectory Shaping Guidance，TSG）能同时满足终端位置约束和终端角度约束，且工程适用性强，因此常被用于具有终端角度约束的制导问题，根据文献[63]，其表达式为(https://www.chuimin.cn)
式中，kp，kq，km——制导参数，其表达式为
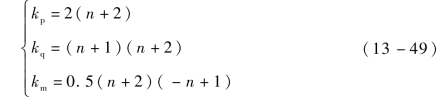
式中，n——制导阶次，一般可取0、1和2。制导阶次n越大，在初始段的需用过载就越大，弹道就越弯曲，而在末端的需用过载就越小，弹道就越平直。
将防御弹采用阶次n=0的弹道成型制导律（和目标无协同）与目标-防御弹采用本章的协同非线性拦截制导律（Cooperative Nonlinear Guidance Law，CNGL）的情形进行对比。CNGL中的惩罚系数设为a1=1010、b1=1010、c1=1和d1=5，当防御弹采用TSG时假设目标做匀速直线运动。期望的攻击角度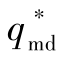
都设为30°。仿真结果如图13-2～图13-5所示，其中下标“1”和“2”分别代表CNGL和TSG。
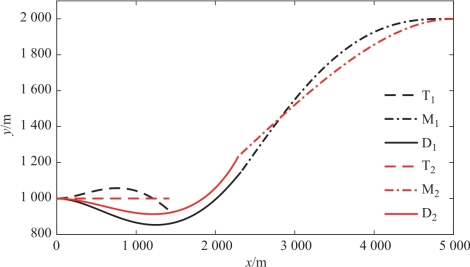
图13-2 CNGL和TSG时的飞行轨迹
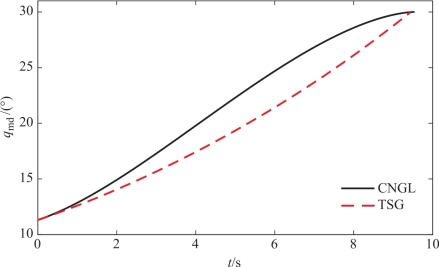
图13-3 CNGL和TSG时qmd的变化曲线
由图13-3可见，无论是采用CNGL还是TSG，防御弹都成功地实现了以期望的攻击角度对攻击弹的拦截。当防御弹和目标采用CNGL时，防御弹-攻击弹视线角速度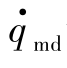
趋于零，同时防御弹最大加速度为41.5 m/s2，而当防御弹采用TSG时，视线角速度
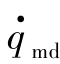并不趋于零，且防御弹最大加速度为52.1 m/s2，大于CNGL时的最大加速度。由此可知，当防御弹与目标间存在双向信息传输时，在目标的协助下，防御弹能以较平直的弹道实现对攻击弹以期望攻击角度的拦截。这是因为，防御弹和目标可进行双向信息传输，目标可将其未来的运动信息传输给防御弹，防御弹在获取目标运动信息后可对攻击弹的未来飞行趋势进行预测并直接向攻击弹飞去；同时，防御弹将其未来的运动信息传输给目标，目标在获取防御弹运动信息后将采取更合理的机动，以协助防御弹。在整个过程中，目标作为诱饵将攻击弹引诱至防御弹附近，同时防御弹通过预测攻击弹的运动趋势直接向攻击弹飞去，最终使得目标和防御弹在付出较小控制能量的前提下成功以期望攻击角度对攻击弹进行拦截。
图13-4 CNGL和TSG时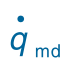
的变化曲线
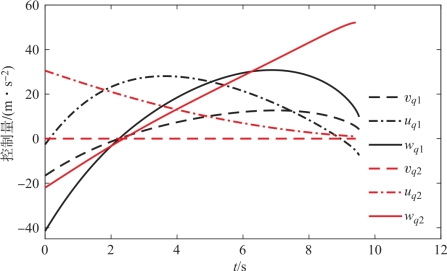
图13-5 CNGL和TSG时控制量的变化曲线
例13-2 本实例给出可得到可行攻击角区域的算例。首先对防御弹以及目标可用过载约束下的可行攻击角区域进行研究，与例13-1类似，惩罚系数设为a1=1010、b1=1010、c1=1和d1=5，目标、攻击弹和防御弹的初始仿真条件同样见表13-1。假设在不同作战场景的目标和防御弹的可用过载不同，防御弹可用过载udmax的范围为4～12，目标可用过载utmax的范围为2～6，防御弹以及目标的安全系数分别为Kd1=1.05和Kt1=1.05，则根据式（13-37）和式（13-38）可分别得到可行攻击角区域与防御弹和目标的可用过载udmax以及utmax之间的关系，如图13-6、图13-7所示。
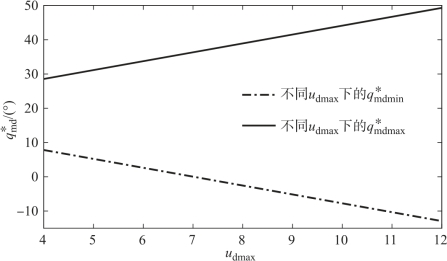
图13-6 不同udmax时的可行攻击角区域
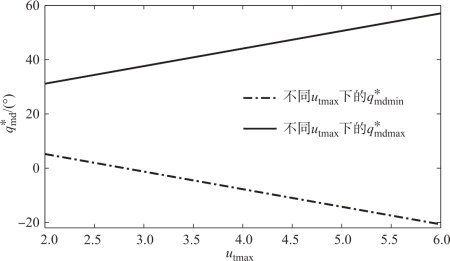
图13-7 不同utmax时的可行攻击角区域
由图13-6、图13-7可知，防御弹的可行攻击角区域随着防御弹或目标的可用过载增加而增加，这也意味着防御弹和目标的可用过载越大，可实现的攻击角区域就越大。需要注意的是，随着可行攻击角区域的不断增加，为实现跨度范围大的可行攻击角区域，某些情况下的防御弹弹道将变得更弯曲，这意味着防御弹将要花费更长的时间对攻击弹进行拦截；如果防御弹拦截攻击弹的时间过长，将导致攻击弹先于防御弹对目标进行攻击，进而导致拦截任务失败。因此，接下来进一步对拦截时间约束下的可行攻击角区域进行研究。
以防御弹和目标可用过载分别为udmax=12和utmax=6为例，由图13-6、图13-7可知，udmax=12以及utmax=6下的可行攻击角区域分别为[-12.93°，49.3°]和[-20.71°，57.08°]，因此在防御弹和目标可用过载同时约束下的可行攻击角区域为[-12.93°，49.3°]和[-20.71°，57.08°]的交集，即[-12.93°，49.3°]。接下来，在[-12.93°，49.3°]区间内选取不同的期望攻击角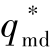
进行仿真分析。选取方法：首先，在[-12.93°，47.07°]区间内每隔5°选择一个点，并同时选择区间的边界点
=49.3°；然后，对所选取的不同期望攻击角
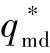分别进行仿真分析，并得到相对应的tgomd0；最后，通过二次函数对
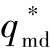和tgomd0之间的关系进行拟合，拟合结果如式（13-50）以及图13-8所示。
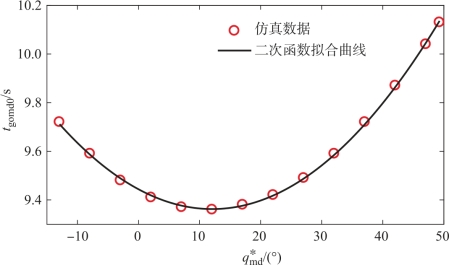
图13-8 tgomd0与
的二次函数拟合曲线
将目标和攻击弹的初始参数代入式（13-40），求解得到攻击弹的初始剩余飞行时间tgomt0为11.331 2 s，同时选择拦截时间裕度ter为1.5 s，则根据式（13-39）可计算得到防御弹的初始剩余飞行时间应满足tgomd0≤9.83 s。接着结合tgomd0≤9.83 s和式（13-50），可求解拦截时间约束下的可行攻击角区域为[-16.92°，41.10°]，最后求解区间[-12.93°，49.3°]和[-16.92°，41.10°]的交集，即可得到最终的可用过载约束udmax=12、utmax=6以及拦截时间约束下的可行攻击角区域，为[-12.93°，41.10°]。
相关文章
- 详细阅读
-
多飞行器协同制导与控制：弹目距离及跟踪指令详细阅读
而且，如果各导弹的rc相同，而各导弹的弹目距离能够跟踪rc，那么在飞行过程中，多枚导弹将同步接近目标，实现位置协同。为控制弹目距离跟踪式（9-7）给定的弹目距离指令，实现多导弹的弹目距离协同，只需设计制导律u，并控制导弹的速度前置角跟踪导弹前置角指令σc。......
2025-09-29
-
多飞行器协同控制成果详细阅读
在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。......
2025-09-29
-
多飞行器协同制导与控制：基于弹间通信的末制导详细阅读
当应用12.2节中的协同末制导律时，在进入末制导前，各导弹可通过信息共享来确定共同的理想飞行时间。本节介绍在飞行过程中弹间存在通信的协同制导律。类似于第8章，末段切换为比例导引律后，各弹之间不再存在协同，因此不能保证n枚导弹在精确同一时间到达目标。表12-2两枚导弹末制导初始参数采用平均弹目距离作为理想弹目距离，仿真结果如图12-10～图12-20所示。......
2025-09-29
-
多飞行器协同制导控制技术-成果详细阅读
多飞行器编队飞行可极大地提升目标搜索、抗电磁干扰及突防能力，是多飞行器协同作战的关键技术。关于多飞行器的编队控制模式，目前主要有虚拟结构模式、基于行为的模式和“领-从”模式。在“领-从”模式中，编队中的某一成员作为领导者，负责编队的航迹规划和生成、目标探测等任务，而其余成员作为跟随者跟踪领导者飞行，以实现编队队形的形成、保持和变换。不同的通信模式和编队控制模式对应不同的编队控制技术。......
2025-09-29
-
多飞行器协同避碰控制策略详细阅读
针对此问题，根据预设性能控制器可将系统误差控制在满足性能函数上下边界范围内的特点，可通过合理地设置性能指标函数来实现弹间的避碰。接下来，将上述性质应用于多弹编队成员间避碰策略的设计中。......
2025-09-29
-
多智能体飞行器协同制导控制详细阅读
MPSP技术的目的：得到合适的控制历程Uk，使得在最后一步（k=N）时的输出YN趋近于理想的输出，YN→，同时付出的控制量最小。MPSP技术需要一个初始猜测控制量，然后根据末端误差来不断修正控制量，最后得到满足要求的控制量。式、式构成了约束条件下的静态规划问题。根据静态规划理论可得因此，在k=1，2，…，N-1时，更新后的控制变量为MPSP算法将动态优化问题转化为静态优化问题进行求解，使优化问题大大简化，计算效率大幅度提升。......
2025-09-29
-
信息与控制: 多飞行器协同制导详细阅读
信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致，必须存在一个各导弹共同关心的变量，这称为信息状态。此外，还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法，这称为一致性算法。因此，可将一致性理论应用于多导弹编队，基于一致性算法来设计导弹的编队控制算法。......
2025-09-29
相关推荐