首页理论教育多飞行器协同制导求解

多飞行器协同制导求解

2023-08-02 理论教育版权反馈

【摘要】：由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。

由式（13-9）、式（13-10）可知，哈密顿函数为

式中，λ11和λ12为协态量，其正则方程为

λ11和λ12在末端时刻满足的横截条件为

式中，

由式（13-12）和式（13-13），可解得协态量λ11和λ12为

式中，χ=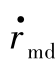 pagenumber_ebook=202,pagenumber_book=193 （tf-t）/rmd≈-1。

由极小值原理可知

联立式（13-11）和式（13-15），可解得

式中，——防御弹和目标的开环解。

由于λ12包含x11（tf）和x12（tf）项，因此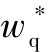 pagenumber_ebook=202,pagenumber_book=193 和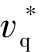不能由当前时刻的状态进行求解，需要求解x11（tf）和x12（tf）的表达式，将式（13-16）代入式（13-9）的第二个方程，并由t到tf进行积分，可得x12（tf）的表达式为

式中，Φ1（·）——状态转移矩阵。

同时，由式（13-17）可知x12（t）的表达式为

将式（13-18）代入式（13-9）的第一个方程，同样由t到tf进行积分，可得

进一步将式（13-17）、式（13-19）整理为x11（tf）和x12（t）的二元一次方程为

式中，系数A1、B1、C1、D1、E1和F1的表达式分别为

式中，。

通过求解式（13-20），可得x11（tf）和x12（tf）的表达式为

将式（13-21）代入式（13-22），可得x11（tf）和x12（tf）的最终表达式；将得到的x11（tf）和x12（tf）的表达式代入式（13-14），可得λ12的表达式；将λ12代入式（13-16），即可得到防御弹和目标加速度的闭环解。