【摘要】:当应用12.2节中的协同末制导律时,在进入末制导前,各导弹可通过信息共享来确定共同的理想飞行时间。本节介绍在飞行过程中弹间存在通信的协同制导律。类似于第8章,末段切换为比例导引律后,各弹之间不再存在协同,因此不能保证n枚导弹在精确同一时间到达目标。表12-2两枚导弹末制导初始参数采用平均弹目距离作为理想弹目距离,仿真结果如图12-10~图12-20所示。
当应用12.2节中的协同末制导律时,在进入末制导前,各导弹可通过信息共享来确定共同的理想飞行时间。但在飞行过程中,导弹间并不存在通信,每枚导弹只要实现指定的理想攻击时间,即可实现协同打击。本节介绍在飞行过程中弹间存在通信的协同制导律。高超声速飞行器的速度大小不可控且不断变化,因此对于多高超声速飞行器来讲,只能通过控制速度的方向来实现协同,与第9章和第10章的思路类似,可通过弹目距离协同的方法来实现高超声速飞行器的协同飞行。影响弹目距离变化的因素有飞行速度的大小、飞行速度与视线之间的夹角(速度前置角),虽然高超声速飞行器的飞行速度大小不可控,但是可通过调整速度前置角来实现弹目距离的控制和跟踪。因此,本章同样采用弹目距离跟踪的思路来设计高超声速飞行器的协同制导律,与第9章和第10章的不同之处在于,各导弹跟踪的理想弹目距离设计方法不同。
为了实现对纵向攻击角度的约束,导弹在纵向采用具有攻击角度约束的制导律(式(12-9)),在纵向制导律已定的情况下,通过调整侧向速度前置角来实现对弹目距离的调整和跟踪。假定n枚助推滑翔高超声速导弹协同飞行,其中第i枚导弹的弹目距离表示为ri,则n枚导弹的平均弹目距离r¯为

如果ri(i=1,2,…,n)与r¯相等,就意味着n枚导弹的弹目距离相等,多导弹同步接近目标,实现了飞行位置协同。当距离目标很近时,在某一弹目距离r,为了确保攻击目标的精度,令导弹转入比例导引律。此处各导弹跟踪的理想弹目距离是所有导弹弹目距离的平均值,既不同于第9章中的基于理想攻击时间设计的理想弹目距离,也不同于第10章中的从弹以领弹的弹目距离作为理想弹目距离。在第10章中,由于领弹采用比例导引律攻击目标,所以其弹目距离一定趋于零,各从弹只要能跟踪领弹的弹目距离,就一定能同时命中目标,因此临近目标时没有进行切换。在本章,各导弹的理想弹目距离为平均弹目距离。需要注意的是,当攻击静止目标时,只要各导弹的速度前置角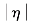 <90°,导弹的相对速度就一定小于零,弹目距离一定是减小的,则平均弹目距离也一定是减小的,最终会趋于零。但是,如果某几枚导弹的
<90°,导弹的相对速度就一定小于零,弹目距离一定是减小的,则平均弹目距离也一定是减小的,最终会趋于零。但是,如果某几枚导弹的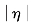 虽然小于90°但是比较大(如80°),则这几枚导弹的弹目距离减小得很慢,平均弹目距离趋于零的速度也就很慢,这几枚导弹为了实现弹目距离协同就会进行大的侧向绕飞,当距离目标比较近时,这是不利的,因此此时就转入比例导引律,以确保对目标的有效攻击。类似于第8章,末段切换为比例导引律后,各弹之间不再存在协同,因此不能保证n枚导弹在精确同一时间到达目标。但是,由于转入比例导引律时的弹目距离比较近,高超声速导弹的速度又很快,因此末段比例导引引起的攻击时间差比较小,各弹还是能够实现几乎在同一时间到达目标,实现对目标的协同攻击。在飞行位置协同段,也不能将
虽然小于90°但是比较大(如80°),则这几枚导弹的弹目距离减小得很慢,平均弹目距离趋于零的速度也就很慢,这几枚导弹为了实现弹目距离协同就会进行大的侧向绕飞,当距离目标比较近时,这是不利的,因此此时就转入比例导引律,以确保对目标的有效攻击。类似于第8章,末段切换为比例导引律后,各弹之间不再存在协同,因此不能保证n枚导弹在精确同一时间到达目标。但是,由于转入比例导引律时的弹目距离比较近,高超声速导弹的速度又很快,因此末段比例导引引起的攻击时间差比较小,各弹还是能够实现几乎在同一时间到达目标,实现对目标的协同攻击。在飞行位置协同段,也不能将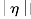 的最大值设置得太小,否则各飞行器的调整能力很小,很难实现飞行位置协同。设置
的最大值设置得太小,否则各飞行器的调整能力很小,很难实现飞行位置协同。设置 的最大值时,要综合考虑框架角约束、导弹的攻角等因素。
的最大值时,要综合考虑框架角约束、导弹的攻角等因素。
在确定理想弹目距离后,就可通过设计偏航方向速度前置角来实现ri对 的跟踪,设计方法同前。本节导弹目标的相对运动关系以及变量定义如图10-1所示。为了内容的完整性,这里给出结果(为了表述方便,以下省略导弹下标i):
的跟踪,设计方法同前。本节导弹目标的相对运动关系以及变量定义如图10-1所示。为了内容的完整性,这里给出结果(为了表述方便,以下省略导弹下标i):

式中,qθ——纵向的视线角;
ηψ0——初始侧向速度前置角;
其余符号意义同前。
采用低通滤波器对ηψc进行滤波,有

式中,ηψd——滤波器的输出,也是ηψ的期望值;
τη——滤波器时间常数,τη>0,考虑到滤波器跟踪性能,τη应足够小。
假设协同作战的导弹为动力学特性、速度特性相差比较大的异构导弹,则将多弹的平均弹目距离作为每个导弹需跟踪的理想弹目距离时的制导律,性能可能会下降。因为各导弹的速度差异较大,对于实现攻击时间协同来讲,在某一时刻,合理的方案是速度快的导弹离目标较远、速度慢的导弹离目标较近,而不是所有导弹的弹目距离相等。如果各导弹在同一时刻、同一弹目距离r转入比例导引,由于各导弹的速度差别较大,就可能造成攻击时间差较大的情况,也就是协同性能下降。针对此种情况,设计每枚导弹的期望弹目距离指令与导弹的速度和弹目距离相关,为

对其求导,得
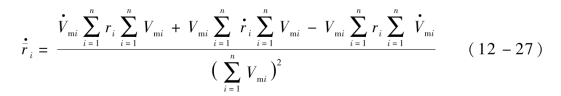
用式(12-26)、式(12-27)替换式(12-23)及其导数,代入式(12-24),即可得到最终的适用于异构飞行器的侧向制导指令。
例12-3 假设两枚导弹(导弹1和导弹2)协同攻击位于(50 000,0,0)(以米(m)为度量单位)处的静止目标,导弹的初始位置、速度等见表12-2(下标“0”表示末制导初始时刻)。当弹目距离r=5 000 m时转入比例导引律(比例系数为3)。在协同指令中,kq=0.10,kr=0.10。两枚导弹的理想攻击角度分别为-15°和-30°。
表12-2 两枚导弹末制导初始参数

采用平均弹目距离作为理想弹目距离,仿真结果如图12-10~图12-20所示。
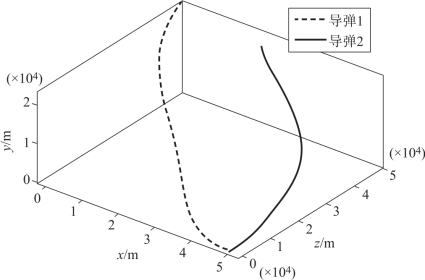
图12-10 两枚导弹的弹道
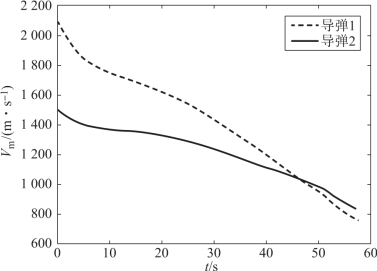
图12-11 两枚导弹的速度变化曲线
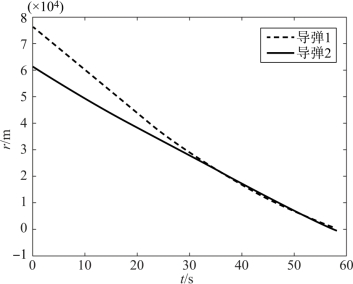
图12-12 两枚导弹弹目距离的变化曲线
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
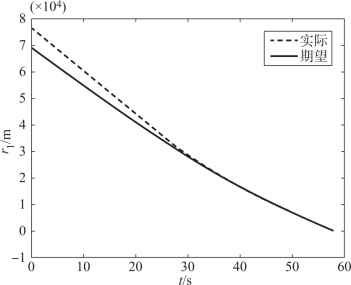
图12-13 导弹1弹目距离的跟踪情况
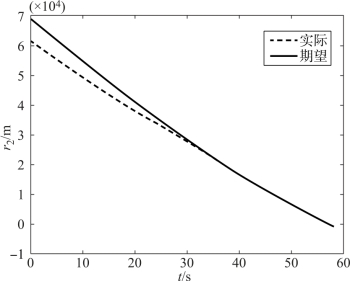
图12-14 导弹2弹目距离的跟踪情况
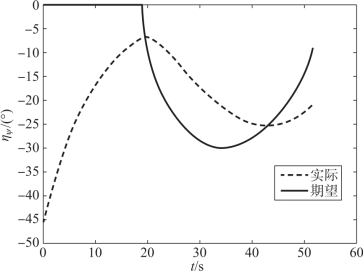
图12-15 导弹1速度前置角的跟踪指令情况
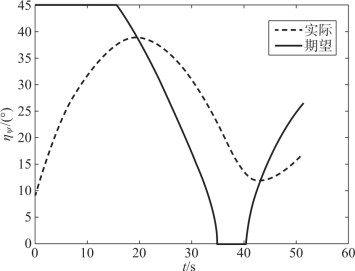
图12-16 导弹2速度前置角的跟踪指令情况
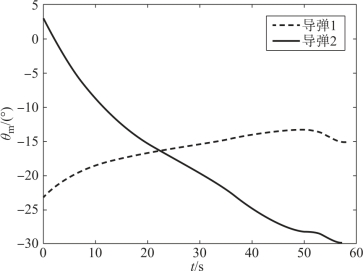
图12-17 两枚导弹的弹道倾角的变化曲线

图12-18 两枚导弹的弹道偏角的变化曲线

图12-19 两枚导弹的攻角的变化曲线
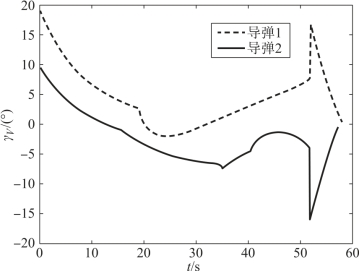
图12-20 两枚导弹的速度倾斜角的变化曲线
假设两枚导弹不采用协同制导律,从一开始就采用比例导引律,则到达目标的时间差为Δt=6.7 s。当采用本章中的协同策略时,由图可见,两枚导弹的攻击时间差为0.8 s,并且均实现了纵向攻击角度的约束。在飞行过程中,两枚高超声速导弹的飞行速度不断变化,命中目标时的速度分别为750 m/s和829 m/s。在飞行过程中,导弹1和导弹2的弹目距离均实现了对平均弹目距离较好的跟踪,实现了飞行位置的协同(由图12-10~图12-14可见)。图12-15、图12-16显示了导弹实际速度前置角对理想速度前置角的跟踪情况,由图可见,跟踪的精度并不是特别高。这是因为,高超声速飞行器开始末制导时,处于20 km左右的高度,大气密度稀薄,因此控制能力较弱,但是从趋势上看,高超声速导弹在尽力实现对指令的跟踪,最后的协同效果也是在可接受范围内。由图12-19、图12-20可见,高超声速导弹的控制量变化较平缓,有利于控制系统的实现。
例12-4 在例12-3中,由于两枚导弹开始末制导时的初始速度大小及方向差别较大,可认为是异构飞行器,因此采用式(12-26)所示的理想弹目距离设计思路,其他仿真条件同例12-3,仿真结果如图12-21~图12-25所示。
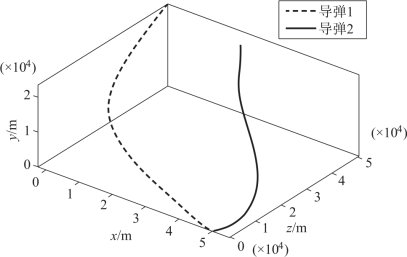
图12-21 两枚导弹的弹道

图12-22 两枚导弹速度的变化曲线
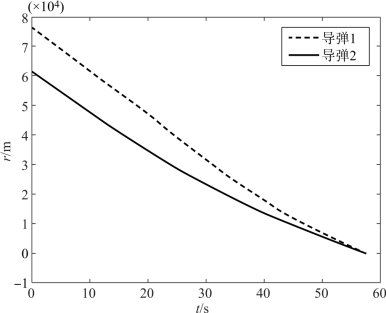
图12-23 两枚导弹弹目距离的变化曲线
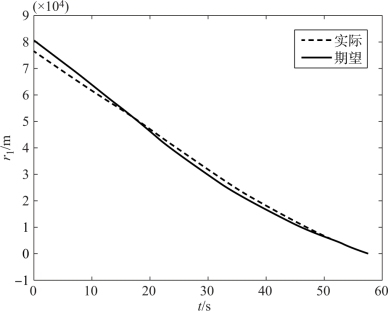
图12-24 导弹1弹目距离的跟踪情况
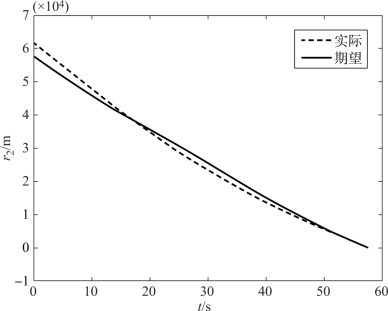
图12-25 导弹2弹目距离的跟踪情况
由仿真结果可知,此时两枚导弹的攻击时间相差0.1 s,相对于例12-3中两枚导弹采用平均弹目距离作为理想弹目距离时的情况,精度提高了87.5%。由图12-23可见,在飞行过程中,两枚导弹的弹目距离不再存在相等的情况,导弹1的弹目距离大于导弹2的弹目距离,而导弹1的飞行速度大于导弹2的飞行速度,因此这种情形更有利于飞行时间的协同,结果也证明了这一点。其他分析与例12-3类似,在此不再赘述。


 的跟踪,设计方法同前。本节导弹目标的相对运动关系以及变量定义如图10-1所示。为了内容的完整性,这里给出结果(为了表述方便,以下省略导弹下标i):
的跟踪,设计方法同前。本节导弹目标的相对运动关系以及变量定义如图10-1所示。为了内容的完整性,这里给出结果(为了表述方便,以下省略导弹下标i):


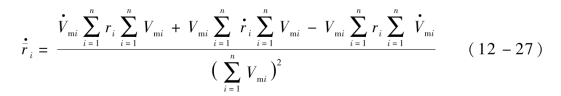




 (https://www.chuimin.cn)
(https://www.chuimin.cn)


















相关推荐