飞行器协同制导：末制导初始位置域解析

2023-08-02 理论教育版权反馈

【摘要】：改变期望协同攻击时间Td1，即可分别计算其对应的初始位置域。

由于各高超声速导弹的机动能力有限，且通常对其末速也有要求，而本章通过控制多导弹攻击时间一致来实现协同，因此其并不是从任何位置开始末制导都能以同一时间实现协同的，有必要在考虑导弹有限机动能力和末速约束的前提下研究各自在不同协同攻击时间对应的末制导可行初始位置域。在本章，当导弹滑翔至z0=h0的高度时，转入末制导，且假设进入末制导时导弹的速度大小和方向已确定。接下来，首先，选定合适的理想攻击时间；然后，在y=y0的前提下求解理想攻击时间对应的x方向的一维可行位置域；最后，求解x、y方向的二维可行位置域。

12.2.2.1　攻击时间范围求解

当目标信息和末制导初期导弹的位置及速度确定后，受可用过载np和要求的最小末速Vfmin的约束，导弹能够实现的飞行时间是有限的，即存在最小攻击时间和最大攻击时间。

由于高超声速导弹速度时变且不可控，其攻击时间范围[tmin，tmax]无法采用解析方法进行求解，因此本章采用数值计算方法对其求解。当导弹采用如式（12-10）所示的带落角约束的三维比例导引律时，其攻击时间T0为最小攻击时间，即tmin=T0。在最小时间的基础上，令Td=T0+iΔt（i=1，2，3，…，Δt为时间间隔）。从i=1开始计算Td，通过仿真来判断导弹采用式（12-14）所示的协同末制导律时是否满足过载n≤np及末速Vf≥Vfmin的约束。若满足，则增加i从而增大Td进行再次仿真；若不满足，则输出上一步的满足约束的Td，将其作为最大攻击时间tmax。通过以上方法，即可求得在某个末制导初始位置下导弹的攻击时间范围。

12.2.2.2　一维可行初始位置域求解

本小节给出导弹末制导一维可行初始位置域的求解方法。假定导弹进入末制导时的位置y0、z0已确定，选取合理的理想协同攻击时间Td1，之后求解能够以Td1实现协同的x0的范围，即一维可行初始位置域。

接下来，分析导弹位于不同末制导初始位置时的协同可行性。假设两枚导弹分别位于位置M1（x011，y0，z0）和M2（x012，y0，z0），且0＜x011＜x012，由于目标位于原点，因此其初始弹目距离r011＜r012。通过12.2.2.1节介绍的方法可以分别计算得到其攻击时间范围[t11min，t11max]和[t12min，t12max]，而对于采用式（12-14）所示制导律的导弹来说，有t11min＜t12min、t11max＜t12max。当t11max＜t12min时，这两个位置对应的攻击时间范围无交集，则M1与M2的导弹无法实现协同；当t11max＞t12min时，导弹可以在[t12min，t11max]中的任一时间实现协同；当t11max=t12min=Td1时，位于M1与M2的导弹仅能以Td1实现协同。考虑多弹协同，由上述分析可知，当t11max=t12min=Td1且多弹初始位置在M1与M2之间时，其均能以Td1实现协同，此时M1与M2在x方向的坐标范围[x011，x012]即最大可行末制导初始位置域。

综上所述，求解一维可行位置域即求解最大攻击时间等于Td1的x011与最小攻击时间等于Td1的x012。以导弹x方向初始位置x0为设计变量，即

考虑导弹的可用过载与末速约束，有

pagenumber_ebook=182,pagenumber_book=173

导弹实现协同的条件为以相同攻击时间Td1击中目标，则性能指标函数可设为

式中，t1——实际飞行时间。

由式（12-20）～式（12-22）构成了优化模型，可采用优化算法（如文化算法）对其求解。在每次优化过程中，计算此时（第j次迭代）的设计变量对应的攻击时间范围[t1jmin，t1jmax]（j=1，2，…，q，q为最大迭代次数）。令性能指标函数中的t=t1jmin，则优化计算可得到x01max；令t=t1jmax，则优化计算可得到x01min。此时，得到攻击时间Td1所对应的一维末制导可行初始位置域[x01min，x01max]。改变期望协同攻击时间Td1，即可分别计算其对应的初始位置域。

12.2.2.3　二维可行初始位置域求解

仍然假设末制导初始时刻导弹的飞行高度z0=h0确定。考虑导引头的作用距离、开始末制导时的高度、导弹侧向机动能力等因素，设定x方向的初始位置范围[x02l，x02h]，在此基础上，将二维可行域的求解问题转化为一维可行域的求解，即取x02k∈[x02l，x02h]（k=1，2，…，q，q＞0），基于12.2.2.2节的方法可求解导弹的末制导初始x0=x02k、z0=h0时，对应于理想攻击时间Td2的y方向坐标范围[y02kmin，y02kmax]。考虑在整个[x02l，x02h]范围内对应的[y02kmin，y02kmax]，则可获得二维末制导可行初始位置域。

例12-2　假设高超声速导弹滑翔至h0=20 km时转入末制导，令初始侧向坐标y0=0。分别设导弹C与导弹D的初始速度为VC0=1 600 m/s与VD0=1 500 m/s。其他初始条件与例12-1相同。为了研究方便，令理想攻击时间Td1（s）在[26，34]中每隔1 s取值。约束条件Vfmin=700 m/s，nP=30。计算结果如表12-1和图12-8所示。

表12-1　一维可行初始位置域

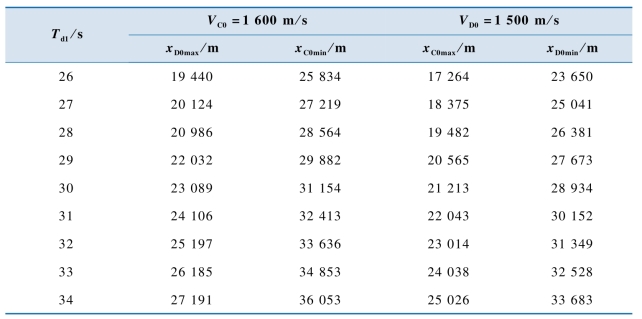
pagenumber_ebook=183,pagenumber_book=174

由表12-1与图12-8可知，对应着不同的理想攻击时间，两个导弹均具有各自的可行初始位置域。由表12-1可知，由于导弹C的初始速度大于导弹D的初始速度，因此有xC0min＞xD0min，xC0max＞xD0max。由于导弹D的初始速度较小，但其也必须满足末速要求，因此其初始位置域较小。例如，当Td1=30 s时，导弹C的可行位置域范围为8.065 km，导弹D只有7.721 km。另一方面，理想攻击时间越大，导弹可调整的范围就越大，其可行初始位置域也越大。

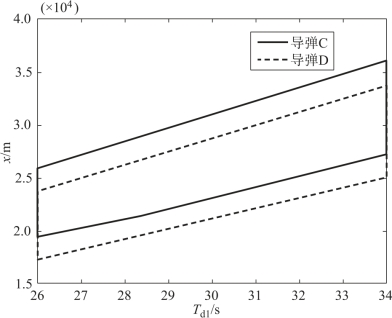
pagenumber_ebook=184,pagenumber_book=175

图12-8　两枚导弹的一维可行初始位置域

以导弹C为例，求解其二维可行位置域。同样假设其在高度为20 km处转入末制导。参考上述求得的一维可行位置域，同时为了计算方便，设导弹C在x方向的初始坐标xC0∈[xC0l，xC0h]=[20，30]。令xC0在[xC0l，xC0h]中每隔1 km取值，其他初始条件与例12-1中相同，求对应的侧向坐标范围。设定理想攻击时间Td2分别为28 s、30 s和32 s，得到二维可行初始位置域如图12-9所示。

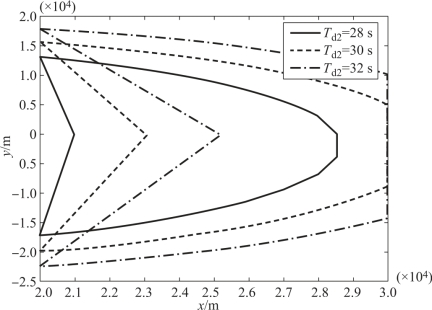
pagenumber_ebook=184,pagenumber_book=175

图12-9　不同Td2时的二维可行初始位置域

当Td2=28 s时，由表12-1可知，在yC0=0前提下，xC0（km）范围为[20.986，28.564]；当没有yC0=0的约束，求取二维可行初始位置域时，在20 km≤xC0＜20.986 km也存在可行位置域，但由图12-9可知，此时的可行yC0是不连续的。较小的xC0对应的可行较大，随着xC0的减小，可行yC0的范围减小，这是因为小的xC0和大的对应着相差不大的初始距离，才有可能实现同一攻击时间。当20.986 km≤xC0≤28.564 km时，其对应着连续可行yC0，随着xC0的增大，可行yC0的范围减小，同样是因为相差不大的初始弹目距离才有可能达到相同的攻击时间。而当xC0＞28.564 km时，初始弹目距离较大，导弹不做机动时的攻击时间已经大于理想攻击时间，故而无可行初始位置域。当Td2=30 s，32 s时，与上述分析类似。

由表12-1可知，Td2=28 s，30 s，32 s时，其一维可行初始位置域（km）的交集为[25.197，28.564]，在此范围内，Td2越大，同一xC0对应的yC0范围就越大，这是因为理想攻击时间越长，导弹能进行调节的时间和余地就大，因此其可行初始位置域也大。

由于本制导律需要在每个制导周期对飞行末端的弹目距离以及弹目距离变化率进行预测，基于此预测值进行剩余飞行时间的估算，因此考虑弹上在线实施，算法的计算速度就是一个需要重点考虑的问题。算法的计算速度可从软件和硬件两个方面考虑：从软件的角度，可对软件结构和程序编码进行优化；从硬件的角度，就是提升硬件的计算和存储能力。总之，科学技术的不断发展、软硬件水平的不断提高及人工智能技术的应用，都为此算法的在线实现提供了光明的前景。

飞行器协同制导：末制导初始位置域解析

相关推荐