【摘要】:本章在此基础上,考虑攻击角度的约束,给出能够同时实现攻击时间约束和攻击角度约束的末制导律。因此,导弹在预测时采用三维制导律表达式为不同于文献[58]中通过纵向弹道的调整来实现攻击时间约束,本章通过在侧向制导指令中加入理想攻击时间与预测攻击时间的误差作为反馈项来实现对攻击时间的控制,而在纵向采用式所示的偏置比例导引律来实现对攻击落角的控制。
高超声速导弹的速度在不断变化且不可控,这为多导弹协同末制导律的设计带来了很大的挑战。文献[58]以导弹每个时刻的状态量为基础,对终端时刻的弹目距离和弹目距离变化率进行预测,通过预测值来计算剩余飞行时间,将其与给定剩余攻击时间的差作为反馈来得到制导指令,从而实现攻击时间的控制。本章在此基础上,考虑攻击角度的约束,给出能够同时实现攻击时间约束和攻击角度约束的末制导律。
对于速度时变的高超声速导弹,其剩余飞行时间的高精度估计是一个难题,文献[58]采用数值计算的方法对其进行在线估计。具体过程如下:
第1步,导弹采用三维比例导引律攻击目标,实际剩余飞行时间与剩余飞行时间预测值分别为tPNG和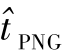 ,当前飞行时间为t,则TPNG=t+tPNG和
,当前飞行时间为t,则TPNG=t+tPNG和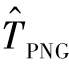 =t+
=t+ 分别为导弹实际飞行时间与导弹飞行时间预测值。在此基础上,剩余弹目距离预测值可表示为
分别为导弹实际飞行时间与导弹飞行时间预测值。在此基础上,剩余弹目距离预测值可表示为
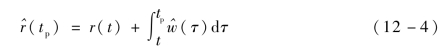
式中,tp——预测时刻;
 ——预测距离变化率。
——预测距离变化率。
由于在命中时刻的弹目距离为0,因此有

第2步,为了得到剩余飞行时间预测值,建立性能指标函数为

采用梯度下降法对式(12-6)所示的无约束优化问题求解,得到
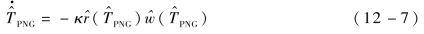
式中,κ——预测系数,κ>0。
由于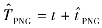 ,因此式(12-7)可写为
,因此式(12-7)可写为
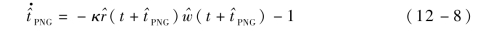
基于式(12-8),可对剩余飞行时间进行在线估计。
文献[58]中,在采用数值方法对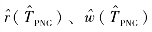 进行预估时,假设导弹在纵侧向均采用常规比例导引律,本章为了进一步考虑攻击角度的约束,在对这两个值进行预估时,假设导弹在侧向仍然采用常规比例导引律,而在纵向采用文献[59]中带落角约束的偏置比例导引律,其表达式为
进行预估时,假设导弹在纵侧向均采用常规比例导引律,本章为了进一步考虑攻击角度的约束,在对这两个值进行预估时,假设导弹在侧向仍然采用常规比例导引律,而在纵向采用文献[59]中带落角约束的偏置比例导引律,其表达式为
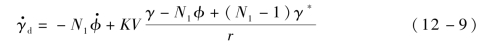
式中,γ*——理想落角;
N1——比例系数;
K——制导参数,K>0。
因此,导弹在预测时采用三维制导律表达式为
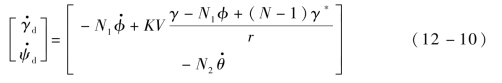
不同于文献[58]中通过纵向弹道的调整来实现攻击时间约束,本章通过在侧向制导指令中加入理想攻击时间与预测攻击时间的误差作为反馈项来实现对攻击时间的控制,而在纵向采用式(12-9)所示的偏置比例导引律来实现对攻击落角的控制。
考虑攻击时间约束,令攻击时间误差为

式中,Tr——为使导弹的指令较平滑而设计的理想攻击时间函数,其表达式为
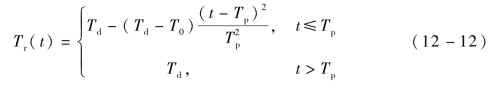
式中,T0——基于运动初始状态采用常规比例导引律的攻击时间;
Tp——控制T0到Td变化速度的时间参数。
将式(12-11)所示的时间误差作为反馈项引入侧向比例导引律指令,有
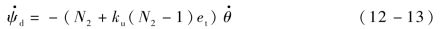
式中,N2——比例系数;
ku——设计参数。
侧向攻击时间控制思路:在每个制导周期,基于常规比例导引律进行预测,通过预测结果对剩余飞行时间进行计算估计,将计算得到的剩余飞行时间与理想剩余飞行时间的差et作为反馈项引入侧向制导律,此制导律作用于弹体后,导弹在下一周期的运动状态已经与预测弹道在下一周期的运动状态不同,将新的运动状态作为初始条件继续预测,同时继续通过et对导弹进行控制,直至最终实现在理想攻击时间击中目标。
三维空间的同时具有攻击时间约束和攻击角度约束的制导律为

在MATLAB环境中调用fmincon函数寻优得到攻角指令,有

式中,L——实际升力。
将式(12-2)中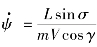 中的
中的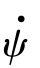 与L替换为
与L替换为 与Ld,可得倾侧角指令的表达式为
与Ld,可得倾侧角指令的表达式为

在本章中,由于重点是制导律的设计,故此处假设导弹具有理想控制系统(即实际攻角与倾侧角能够理想跟踪攻角指令与倾侧角指令),即

至此,得到了导弹的控制量,再代入运动方程组,即可实现对导弹的控制。
例12-1 假设目标位于原点,导弹A、B的初始位置(以千米(km)为度量单位)分别为(x0A,y0A,z0A )=(25,5,20),(x0B,y0B,z0B )=(28,-10,20)。两枚导弹的初始速度均为V0=1 600 m/s,初始弹道倾角均为γ0=-10°,初始弹道偏角均为ψ0=-80°。升力系数和阻力系数为
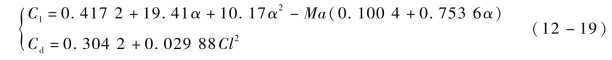
导弹的质量为m=1 600 kg,参考面积为S=0.502 6 m2。攻角和倾侧角的允许范围分别为[-15°,15°]和[-90°,90°]。在制导律中,N1=N2=3,κ=8×10-6,ku=10,K=-1.5。理想攻击时间Td=30 s,理想落角γ*=-80°。仿真结果如图12-2~图12-7所示。
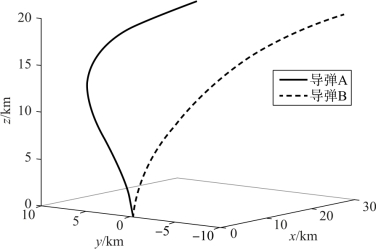
图12-2 两枚导弹的弹道曲线
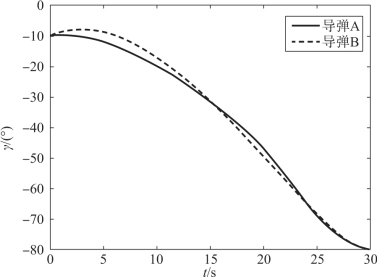
图12-3 两枚导弹弹道倾角的变化曲线
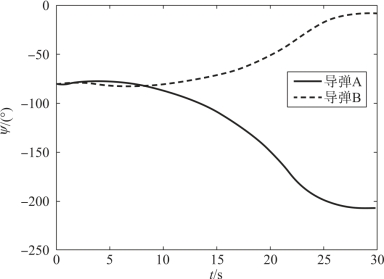
图12-4 两枚导弹弹道偏角的变化曲线
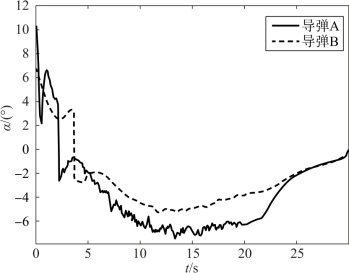
图12-5 两枚导弹攻角的变化曲线
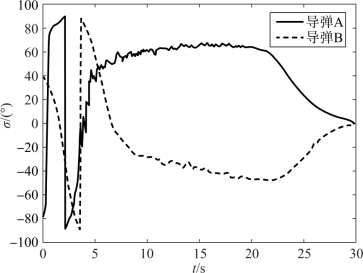
图12-6 两枚导弹倾侧角的变化曲线
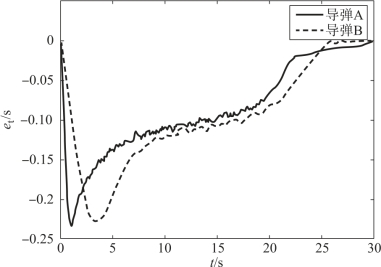
图12-7 两枚导弹et的变化曲线
由图12-2、图12-3可知,两枚导弹均在指定的攻击时间30 s以指定落角-80°命中了目标,实现了对目标的协同攻击。由图12-5、图12-6可知,导弹的控制量均在给定的范围内变化。以导弹A为例进行分析,由图12-7可见,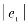 由初值0快速增加,由于导弹通过侧向运动实现攻击时间的调整,且在开始一段时间升力较小(飞行高度高),因此导弹在初始时的倾侧角较快增大,如图12-6所示。随着
由初值0快速增加,由于导弹通过侧向运动实现攻击时间的调整,且在开始一段时间升力较小(飞行高度高),因此导弹在初始时的倾侧角较快增大,如图12-6所示。随着 减小,当V
减小,当V +g cosγ<0时,升力指令随之改变符号,攻角与倾侧角均发生翻转。为了实现要求的较大落角,在末制导开始后的一段时间(如10~20 s)内,导弹以较大的负攻角飞行,使弹道下压,最终实现落角约束。由于导弹在纵侧向运动存在着耦合,因此,为了实现指定的攻击时间,倾侧角就较大,导弹绕弯(由图12-6可见)。综合纵侧向指令的耦合变化,最终实现了在三维空间内,导弹以指定的攻击时间和落角命中目标。导弹B的情况可类似分析。
+g cosγ<0时,升力指令随之改变符号,攻角与倾侧角均发生翻转。为了实现要求的较大落角,在末制导开始后的一段时间(如10~20 s)内,导弹以较大的负攻角飞行,使弹道下压,最终实现落角约束。由于导弹在纵侧向运动存在着耦合,因此,为了实现指定的攻击时间,倾侧角就较大,导弹绕弯(由图12-6可见)。综合纵侧向指令的耦合变化,最终实现了在三维空间内,导弹以指定的攻击时间和落角命中目标。导弹B的情况可类似分析。

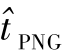 ,当前飞行时间为t,则T
,当前飞行时间为t,则T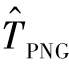 =t+
=t+ 分别为导弹实际飞行时间与导弹飞行时间预测值。在此基础上,剩余弹目距离预测值可表示为
分别为导弹实际飞行时间与导弹飞行时间预测值。在此基础上,剩余弹目距离预测值可表示为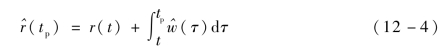
 ——预测距离变化率。
——预测距离变化率。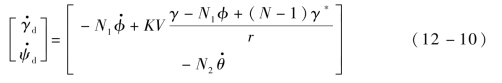
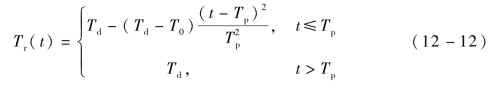

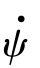 与L替换为
与L替换为 与L
与L

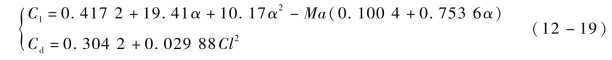






 +g cosγ<0时,升力指令随之改变符号,攻角与倾侧角均发生翻转。为了实现要求的较大落角,在末制导开始后的一段时间(如10~20 s)内,导弹以较大的负攻角飞行,使弹道下压,最终实现落角约束。由于导弹在纵侧向运动存在着耦合,因此,为了实现指定的攻击时间,倾侧角就较大,导弹绕弯(由图12-6可见)。综合纵侧向指令的耦合变化,最终实现了在三维空间内,导弹以指定的攻击时间和落角命中目标。导弹B的情况可类似分析。
+g cosγ<0时,升力指令随之改变符号,攻角与倾侧角均发生翻转。为了实现要求的较大落角,在末制导开始后的一段时间(如10~20 s)内,导弹以较大的负攻角飞行,使弹道下压,最终实现落角约束。由于导弹在纵侧向运动存在着耦合,因此,为了实现指定的攻击时间,倾侧角就较大,导弹绕弯(由图12-6可见)。综合纵侧向指令的耦合变化,最终实现了在三维空间内,导弹以指定的攻击时间和落角命中目标。导弹B的情况可类似分析。




相关推荐