为了避免导弹控制指令变化过于剧烈，可令xr、在过渡段连续变化。......
2023-08-02
多飞行器导引控制：11.3小节
【摘要】：为了使导弹以设计的相对距离跟踪导引点飞行，需设计跟踪控制器。表11-1导弹和导引点的初始参数及攻击参数表11-1中G2和G3的初始航向角是在已知G1运动规律的前提下根据攻击时间和攻击速度要求计算得到的。导弹航向角的变化也比较平稳，由数据可知3枚导弹的最大法向过载分别为0.12、0.91和1.35。图11-10导弹2的xr、yr跟随、的变化曲线控制器工作状态良好，它控制导弹与虚拟点的相对距离xr、yr快速、稳定地跟踪设计的理想相对距离。
为了使导弹以设计的相对距离跟踪导引点飞行，需设计跟踪控制器。由式（11-5）、式（11-6），可得
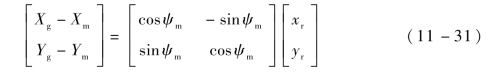
假设所设计的理想的相对距离为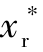
和
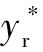，令
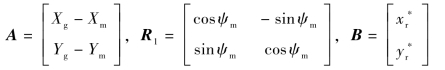
定义相对位置误差为
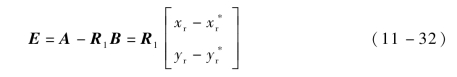
对式（11-32）求导，可得
式中，
如式（11-36）所示的导弹的跟踪控制律满足渐近稳定性质，使误差E趋于零，即实现导弹对导引点按设定相对距离的跟踪飞行。
综上，基于虚拟导引点的多弹协同制导控制方法的设计步骤如下：
第1步，给定目标位置、领弹的理想攻击速度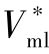
、领弹虚拟点的初始位置、初始航向角，令虚拟点的速度等于理想攻击速度，即Vg=
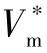，根据式（11-12）～式（11-15）计算出领弹虚拟点的长度L、qg以及导引点到达目标的时间Tg，将此Tg作为弹群的理想飞行时间
。
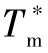第2步，令从弹虚拟点的速度等于从弹理想的攻击速度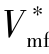
，再根据理想飞行时间
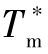，可求得从弹虚拟点的圆弧轨迹长度。在给定从弹导引点初始位置的基础上，根据式（11-13）求得虚拟点的初始航向角。此时，从弹导引点的运动规律唯一确定。
第3步，给定领弹在位置协同段与虚拟点间的理想相对距离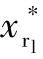
、
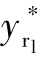；给定领弹的理想攻击角以及re，根据式（11-28）、式（11-29）确定在飞行末段领弹的理想相对距离；设定飞行位置协同结束的条件，获得当时时间t1，设定末段开始时间t2，根据式（11-30）求解过渡段的理想相对距离。
第4步，在飞行位置协同段，根据领弹的弹目距离rc和式（11-17）确定出从弹的理想相对距离；给定从弹的理想攻击角，结合re，计算出在飞行末段从弹的理想相对距离；类似于领弹，根据式（11-30）计算出过渡段的理想相对距离。
第5步，设计控制器，控制领弹和从弹以前述设计出的理想相对距离跟踪各自虚拟点的飞行。
例11-1 假设3枚导弹协同攻击一艘静止的舰艇，舰艇的位置（以千米（km）为度量单位）为（40，40）。导弹Mi（i=1，2，3，下同）及相应的导引点Gi的初始位置（X0，Y0）、初始速度V0、初始航向角ψ0及导弹Mi的理想攻击角q*见表11-1。以导弹1作为领弹，以导弹2、导弹3作为从弹，领弹和从弹的理想攻击速度均为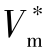
=200 m/s。
表11-1 导弹和导引点的初始参数及攻击参数
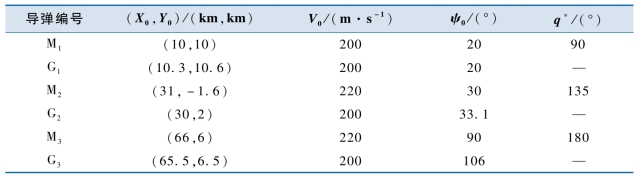
表11-1中G2和G3的初始航向角是在已知G1运动规律的前提下根据攻击时间和攻击速度要求计算得到的。导弹发射后即开始飞行位置协同，在领弹的弹目距离rc≤30 km时结束位置协同飞行，记录此时的时间为t1，在t2=160 s时进入末段飞行，r=re=2 m时引爆战斗部，实现对目标的攻击。位置协同段，领弹按照xr=yr=500 m飞行。3枚导弹的时间常数设为τV=1 s，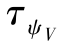
=0.3 s，相对误差动力学方程参数为
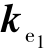=diag（32，32），
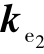=diag（15，15）。仿真结果如图11-4～图11-10所示。
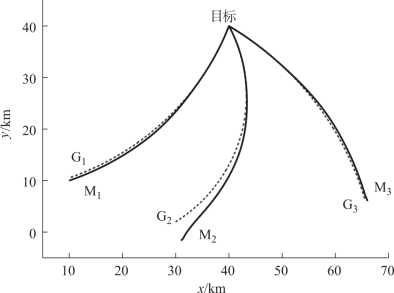
图11-4 导弹弹道及相应虚拟点轨迹
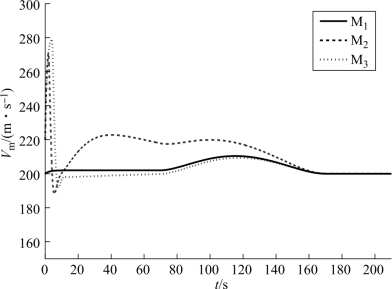
图11-5 飞行速度的变化曲线
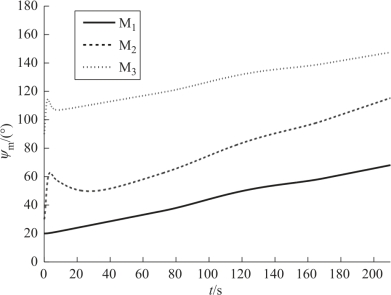
图11-6 航向角的变化曲线
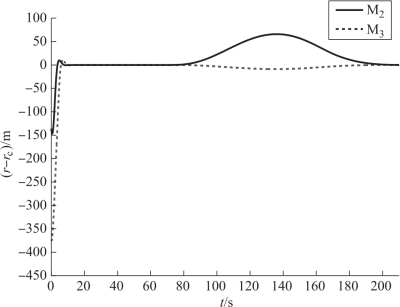
图11-7 弹目距离差的变化曲线
对仿真结果进行分析可知，在飞行时间为215.4 s时，3枚导弹与目标之间的距离均为1.97 m，其攻击速度均为200.0 m/s，攻击角度分别为90.3°、135.3°和179.6°。由此可知，3枚导弹在战斗部威力半径范围内同时到达目标，且实际攻击速度等于理想攻击速度，实际攻击角与理想攻击角之差均小于0.5°。因此，可认为3枚导弹以要求的速度和攻击角度同时命中了目标。由图11-4可见，各导弹虚拟点的轨迹均为圆弧段，各导弹跟随虚拟点飞行。
图11-8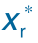 
的变化曲线
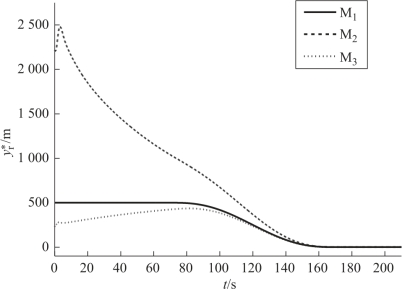
图11-9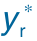 
的变化曲线
M1发射后，M2和M3经过几秒钟的调整，其弹目距离等于领弹的弹目距离，实现了飞行过程中的位置协同，提高了导弹的突防概率，位置协同在80 s左右结束（由图11-7可见）。在实现位置协同时，M1为领弹，因此，其速度变化较M2、M3平稳。在起控后20 s内，M2和M3的速度变化比较大，之后变化相对平稳，由数据知，导弹2和导弹3的最大切向过载均为6.11，M1的最大切向过载为0.08。导弹航向角的变化也比较平稳，由数据可知3枚导弹的最大法向过载分别为0.12、0.91和1.35。因此，无论是需用切向过载还是需用法向过载，都比较小，有利于工程实现。
在进行位置协同时，3枚导弹的xr等于yr，之后进入光滑过渡段，最后一段时间保持在一定的常值上。xr和yr的设计至关重要，它直接关系到导弹在完成协同攻击时的需用切向过载和需用法向过载。在本实例中，xr和yr的变化比较平稳，因此各导弹的需用切向过载和需用法向过载均不大。
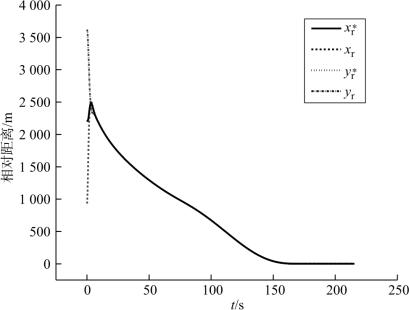
图11-10 导弹2的xr、yr跟随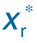
、
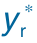的变化曲线
控制器工作状态良好，它控制导弹与虚拟点的相对距离xr、yr快速、稳定地跟踪设计的理想相对距离
。从弹导引点初始位置的选择对从弹的需用过载也有影响，当初始的xr、yr与
相差不大时，从弹的需用过载会比较小。
在本制导控制律中，还可通过对虚拟点初始位置、相对距离的设计来对协同飞行中的避撞问题进一步考虑，设计既能够实现协同飞行又能够避免飞行过程中多飞行器避免碰撞的制导控制方法。
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同控制成果详细阅读
在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
多飞行器协同避碰控制策略详细阅读
针对此问题，根据预设性能控制器可将系统误差控制在满足性能函数上下边界范围内的特点，可通过合理地设置性能指标函数来实现弹间的避碰。接下来，将上述性质应用于多弹编队成员间避碰策略的设计中。......
2023-08-02
-
信息与控制: 多飞行器协同制导详细阅读
信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致，必须存在一个各导弹共同关心的变量，这称为信息状态。此外，还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法，这称为一致性算法。因此，可将一致性理论应用于多导弹编队，基于一致性算法来设计导弹的编队控制算法。......
2023-08-02
-
多飞行器协同制导与控制：成功成果详细阅读
而为了占领战争的优势地位，战争另一方往往发射机动导弹对无人战机进行袭击。如果攻击弹具有强大的威力，那么为了能够成功拦截并摧毁它，则目标可能需发射多枚防御弹进行协同拦截。此时，一方面，涉及防御弹与目标的协同问题；另一方面，涉及多枚防御弹对攻击弹进行协同拦截的问题。......
2023-08-02
-
多飞行器协同制导与控制技术详细阅读
多飞行器协同飞行，当攻击目标时，如果能够从不同的方向同时命中目标，则能够大大提高对目标的攻击性能。要想实现此目的，需有协同末制导律作为技术支撑。进一步，在设计协同末制导律时，还需考虑各导弹的控制量受限、框架角受限等约束问题。对于通过信息传输实现协同攻击的多导弹，信息的传输模式、通信拓扑的设定和信息的利用规则是设计协同末制导律的关键问题。......
2023-08-02
-
多飞行器协同制导与防御弹2控制详细阅读
在目标、防御弹1和防御弹2协同对攻击弹拦截的过程中，目标和防御弹1采用式所示的协同拦截制导律飞行，防御弹2则跟踪防御弹1的弹目距离，最终实现和防御弹1同时拦截攻击弹。因此，当防御弹1与防御弹2距离攻击弹很近时，令防御弹2转为采用式所示的可实现落角约束的弹道成型制导律。......
2023-08-02
相关推荐