由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。......
2023-08-02
多飞行器协同制导设计：导弹-导引点相对距离
【摘要】：为了避免导弹控制指令变化过于剧烈，可令xr、在过渡段连续变化。
在确定导引点轨迹后，通过设计随时间变化的导弹与导引点之间的相对距离xr（t）、yr（t），可实现多导弹之间的位置协同和攻击时间协同，同时满足末端攻击角度的约束和攻击速度的约束。
此处，与第9章类似，为了提高导弹的突防概率，令几枚导弹在某一时间段内从不同的方向同步靠近目标，即使几枚导弹在每一时刻都处于一个以目标为球心的球面上（如果是平面，则是以目标为圆心的圆上），逐渐飞向目标。选多枚导弹中的一枚导弹作为领弹（参考弹），假设其距目标的距离为rc，其他导弹（称作从弹）根据领弹发送的位置信息来调节与导引点的相对距离xr、yr，使其与目标之间的距离也为rc，从而实现多枚导弹从不同的方向同时逼近目标。
令从弹i的弹目距离等于领弹的弹目距离rc，即
将式（11-5）和式（11-6）变形，得到以虚拟点位置、相对距离和航向角ψmi表示的从弹的位置Xmi和Ymi，将其代入式（11-15），假设xr=yr=u，且令
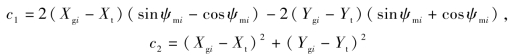
则式（11-15）变换为
求解式（11-16），得
只要c2≤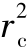
，即从弹导引点距目标的距离小于等于领弹距目标的距离，式（11-17）中的xr、yr就一定有解。由式（11-17）解得的xr=yr有两个值，可根据实际情况选择其中之一。
11.2.2.1 攻击角度控制
在地面坐标系中，有
式中，Vr——导引点与导弹的相对速度。
将式（11-18）投影到地面坐标系的Ox轴和Oy轴，得
当导弹以固定的相对距离（xr、yr为常数）跟随导引点飞行时，有
=0、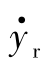
=0，代入式（11-19）、式（11-20），可得
将式（11-21）、式（11-22）两边平方再相加，可得
即
将式（11-24）代入式（11-21）、式（11-22），结合实际情况，可得
由式（11-24）、式（11-25）可知，当导弹以固定的相对距离跟随导引点飞行时，导弹和导引点的速度大小和方向均相同。
当导引点运动至目标时，点G与点T重合。此时，导弹与导引点（目标）之间的相对位置如图11-3所示。
图中的χ为由导弹与导引点之间的相对距离xr、yr决定的相对方位角，有
本章导弹的攻击角定义为末端的视线与Ox轴之间的夹角，即图11-3中的qm，其表达式为
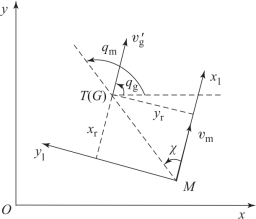
图11-3 导弹-导引点-目标之间的关系图
当确定导引点的运动规律后，就可以根据式（11-13）确定qg。综合式（11-26）、式（11-27）可知，通过设定xr和yr来设定相对方位角χ，最终可实现对导弹攻击角度的控制，即可使导弹以理想的攻击角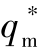
攻击目标。此时，xr和yr之间的关系可根据式（11-26）和式（11-27）确定：
假设战斗部的威力半径为rz，可认为当弹目距离r≤rz时，可通过引爆战斗部导弹来击中目标。假设在r=re（re≤rz）时引爆战斗部，此时有
由上可知，根据式（11-28）、式（11-29）即可确定在飞行末段导弹与导引点之间的相对距离xr和yr。也就是说，在飞行末段，如果导弹与导引点的相对距离保持为由式（11-28）、式（11-29）确定的值，那么可使导弹以理想攻击角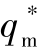
击中目标。
11.2.2.2 攻击速度及攻击时间控制
由式（11-25）可知，在飞行末段，当导弹以固定的相对距离跟踪虚拟点飞行时，导弹的速度等于虚拟点的运动速度。因此，在确定虚拟点的运动速度时，可假设其等于导弹的理想攻击速度，即可满足导弹末端攻击速度的要求。
在已知领弹理想攻击速度
和对应虚拟点的初始位置、初始航向角的基础上，根据式（11-12）、式（11-14）可计算得到其跟随导引点到达目标的时间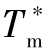
，将此时间作为多弹协同攻击目标的理想攻击时间Td=
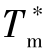。其他从弹则可根据
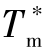和给定的理想攻击速度
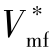来确定其对应导引点的运动轨迹长度，在已知导引点初始位置的基础上，可根据式（11-12）求得初始航向角。此时，从弹的导引点运动规律确定，控制从弹跟随导引点飞行即可实现攻击时间的协同。
11.2.2.3 过渡段相对距离设计
导弹发射后即开始位置协同，其与导引点间的相对距离xr、yr可根据式（11-17）确定；为了实现攻击角度协同，在飞行末段，xr、yr需要按照式（11-28）、式（11-29）来确定；在位置协同结束后，xr、yr需按照一定的规律过渡至末段的值。为了避免导弹控制指令变化过于剧烈，可令xr、
在过渡段连续变化。假设多弹位置协同在t1时刻结束、在t2时刻进入末段攻击，为保证在t1、t2时刻xr、yr以及其一阶、二阶导数连续变化，以xr为例，设
根据已知的t1和t2时刻的值
即可确定式（11-30）中的系数a、b、c、d、e、f，从而确定过渡段xr的变化规律。过渡段yr的确定类似于xr，在此不再赘述。
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同制导与控制：导弹平面运动模型详细阅读
图8-1多枚导弹协同攻击目标的示意图如图8-1所示，虽然每枚导弹的初始弹目距离和初始航向角不同，但协同攻击目标就是要求它们同时到达目标。由于反舰导弹攻击的目标——水面舰艇的机动性和速度无法与高亚声速或超声速反舰导弹相比，因此建模时可以假设目标是静止的。同时，假设导弹的速度恒定且忽略自动驾驶仪的滞后。假设终止时间Tf为理想攻击时间Td，则根据图8-2可得在将aF视为常值的基础上，求解一个控制能量最小的最优控制问题。......
2023-08-02
-
虚拟导引点与导弹相对运动模型详细阅读
导弹与虚拟导引点的相对运动关系如图11-1所示。在地面坐标系中，导弹和导引点的运动学方程为图11-1导弹与导引点的相对运动关系基于参考坐标系与地面坐标系之间的变换关系，可得导弹和导引点之间的相对运动关系为假设导弹具有一阶自动驾驶仪，则有式中，τV，τψm——导弹马赫数自动驾驶仪和航向角自动驾驶仪的时间常数；Vmc，ψmc——导弹的速度指令和航向角指令。......
2023-08-02
-
多飞行器协同制导与控制：相对运动模型解析详细阅读
图13-1目标-攻击弹-防御弹的相对运动关系图中，Vi、θi、ai分别为3个飞行器的速度、弹道倾角以及法向加速度；rmt和qmt分别为攻击弹和目标之间的相对距离和视线角；rmd和qmd分别为防御弹和攻击弹之间的相对距离和视线角；uq和vq分别表示攻击弹和目标垂直于攻击弹-目标视线方向的加速度；wq和分别表示防御弹和攻击弹垂直于防御弹-攻击弹视线方向的加速度。......
2023-08-02
-
多飞行器协同制导与控制：弹目距离及跟踪指令详细阅读
而且，如果各导弹的rc相同，而各导弹的弹目距离能够跟踪rc，那么在飞行过程中，多枚导弹将同步接近目标，实现位置协同。为控制弹目距离跟踪式（9-7）给定的弹目距离指令，实现多导弹的弹目距离协同，只需设计制导律u，并控制导弹的速度前置角跟踪导弹前置角指令σc。......
2023-08-02
-
多飞行器协同制导与控制：附加制导指令确定详细阅读
本节阐述如何确定满足攻击时间要求的附加指令uF。联立式、式，可以得到加速度指令，也就是基于线性模型得出的ITCG导引律，为由式可知，当导弹接近目标时，xgo趋于0，此时上述制导指令会趋于无穷大。表8-14枚导弹的初始参数图8-3给出了4枚导弹采用PNG和ITCG时的弹道对比。在采用PNG时，导弹1、导弹2、导弹3和导弹4的攻击时间分别为35.67 s、30.83 s、27.40 s和31.89 s，4枚导弹采用PNG时的攻击时间差较大，最大攻击时间差为8.27 s。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
信息与控制: 多飞行器协同制导详细阅读
信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致，必须存在一个各导弹共同关心的变量，这称为信息状态。此外，还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法，这称为一致性算法。因此，可将一致性理论应用于多导弹编队，基于一致性算法来设计导弹的编队控制算法。......
2023-08-02
相关推荐