当应用12.2节中的协同末制导律时，在进入末制导前，各导弹可通过信息共享来确定共同的理想飞行时间。本节介绍在飞行过程中弹间存在通信的协同制导律。类似于第8章，末段切换为比例导引律后，各弹之间不再存在协同，因此不能保证n枚导弹在精确同一时间到达目标。表12-2两枚导弹末制导初始参数采用平均弹目距离作为理想弹目距离，仿真结果如图12-10～图12-20所示。......
2023-08-02
多飞行器协同制导与控制：基于MPSP的制导律
【摘要】：需要说明的是，基于10.2节的模型，式中的综上，基于MPSP的三维协同制导律的实现流程如下：第1步，综合考虑弹群中各弹的初始位置及速度，为虚拟领弹设置合适的初始位置及速度。采用MPSP制导律则在原具有攻击时间约束的弹道基础上对其进行了调整，从而实现对攻击角度的约束。表10-4～表10-6给出了4枚从弹分别采用基于弹目距离跟踪的攻击时间协同的制导律和本章提出的同时具有攻击时间约束和攻击角度约束的MPSP制导律时，各导弹的攻击角度情况。
由10.2节的运动模型可知，状态变量为X=[VmθmψVm xm ym zm]T，控制量为U=[ay az]T，输出变量为
，基于MPSP算法思路，通过预测-校正迭代循环来获取新的控制量，使得导弹在t*时刻的输出趋近于理想的终端值
首先对10.2节中的运动模型进行离散化，然后定义末端时刻输出量偏差ΔYN=YN（tf）-YNd（tf）（tf=t*），其他步骤同10.1。需要说明的是，基于10.2节的模型，式（10-6）中的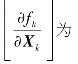
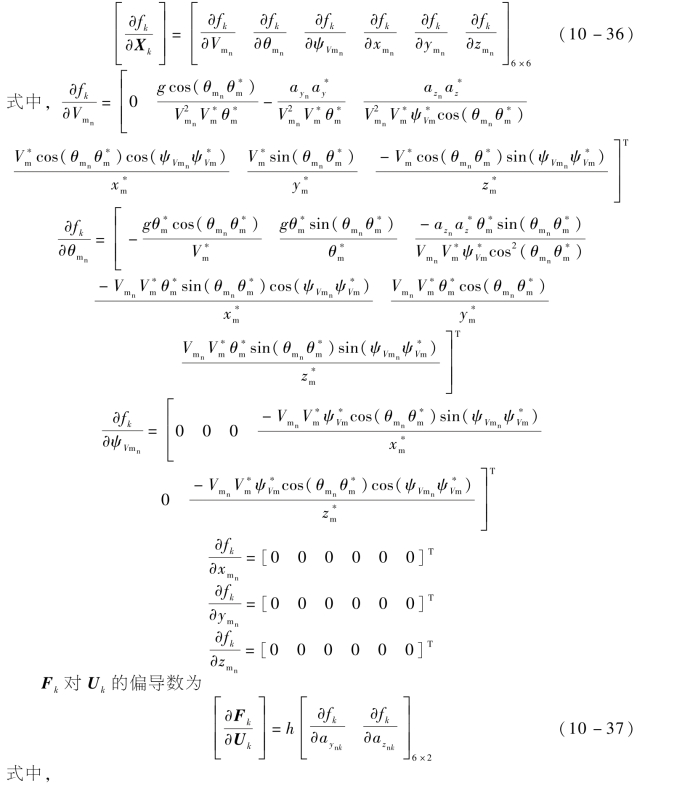
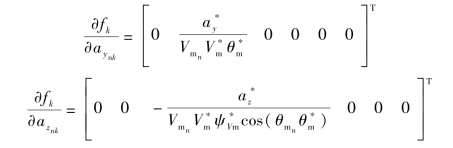
综上，基于MPSP的三维协同制导律的实现流程如下：
第1步，综合考虑弹群中各弹的初始位置及速度，为虚拟领弹设置合适的初始位置及速度。设虚拟领弹采用增强比例导引飞行，虚拟领弹攻击目标的时间即协同攻击时间t*。设定步长h，根据t*和h就可得到终端时刻步数N。
第2步，从弹俯仰通道采用式（10-27）所示的三维增强比例导引指令，侧向采用能够实现对虚拟领弹弹目距离进行跟踪的指令（式（10-31）），此时两个通道的指令就作为MPSP算法的初始猜测控制量。
第3步，基于猜测控制量，采用某数值积分方法对导弹运动方程组进行积分，即进行预测。
第4步，计算末端输出状态YN，根据指定的末端约束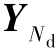
，求出偏差dYN，如果大于设定的门限值则进入第5步，否则退出循环，将此刻的控制量作为最终的控制量输出。
第5步，计算敏感矩阵Bk，k=N-1，N-2，…，1。
第6步，计算Aλ和bλ。
第7步，计算dUk并更新控制变量Uk，将此时的Uk作为猜测控制量，返回第3步。
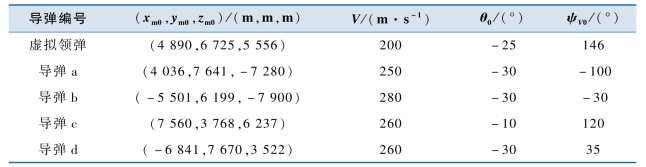
例10-1 假设4枚常速导弹（导弹a、导弹b、导弹c、导弹d）协同攻击位于水平面内的目标，所设计的虚拟领弹及四枚从弹的初始参数见表10-1。
表10-1 虚拟领弹和从弹的初始参数
以米（m）为度量单位，假设目标的初始位置为（0，0，0），令目标分别为静止目标、匀速直线运动目标和蛇形机动目标，具体情况见表10-2。设制导系数K=3，各导弹采用APN攻击不同目标时的攻击时间见表10-3。
表10-2 目标运动情况
表10-3 APN制导时的攻击时间s
由表10-3可见，虚拟领弹采用APN制导时的攻击时间大于各枚从弹采用APN制导时的攻击时间，因此为从弹提供了调整飞行时间的裕度。
虚拟领弹攻击目标的时间t*即弹群的理想攻击时间。为了增强多弹对目标的攻击能力和毁伤效果，指定导弹a、导弹b、导弹c、导弹d的理想攻击角度
分别为（-30°，-140°）、（-20°，-80°）、（-45°，90°）、（-75°，-90°）。
协同策略中k=10、ηψmax=π/4，低通滤波器时间常数τη=0.01，仿真步长为0.01 s，4枚导弹采用基于弹目距离跟踪的攻击时间协同制导律（本章中的初始猜测解）和采用本章设计的MPSP制导律时的弹道如图10-2～图10-4所示。
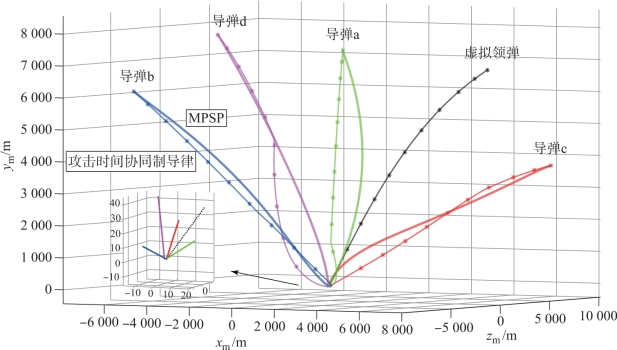
图10-2 协同攻击静止目标1时的弹道图
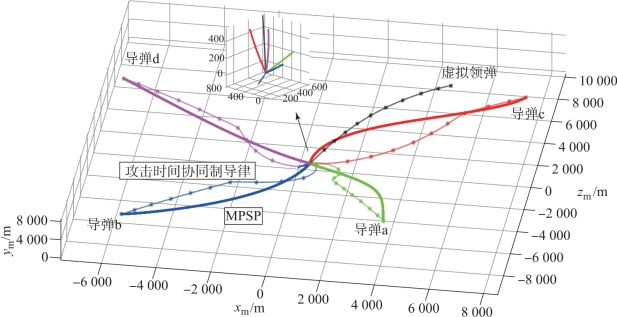
图10-3 协同攻击目标2时的弹道图
图10-4 协同攻击目标3时的弹道图
在攻击目标1、目标2和目标3时，虚拟领弹的时间分别为26.12 s、26.28 s和26.02 s，在这3种情况下，4枚从弹均实现对虚拟领弹弹目距离的跟踪，与虚拟领弹同时到达目标，即4枚从弹实现了在同一时间对目标的攻击。由图10-2～图10-4可知，各弹采用基于弹目距离跟踪的攻击时间协同制导律时，并不能满足攻击角度的约束。采用MPSP制导律则在原具有攻击时间约束的弹道基础上对其进行了调整，从而实现对攻击角度的约束。
表10-4～表10-6给出了4枚从弹分别采用基于弹目距离跟踪的攻击时间协同的制导律（以下简称“攻击时间协同制导律”）和本章提出的同时具有攻击时间约束和攻击角度约束的MPSP制导律时，各导弹的攻击角度情况。
表10-4 协同攻击目标1的攻击角度[（°），（°）]
表10-5 协同攻击目标2的攻击角度[（°），（°）]
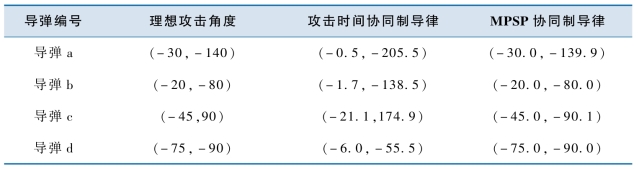
表10-6 协同攻击目标3的攻击角度[（°），（°）]
不失一般性，接下来以导弹c为例，给出两种制导律下的弹道倾角、弹道偏角以及控制量变化曲线。
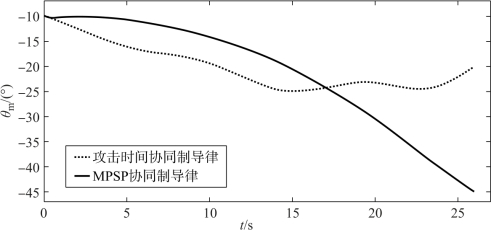
图10-5 弹道倾角θm的变化曲线
图10-6 弹道偏角ψVm的变化曲线
图10-7 控制量ay的变化曲线
由图10-5、图10-6可见，导弹c在两种制导律下的攻击时间相同。攻击时间协同制导律情况下的攻击角度没有达到指定的攻击角度，以图10-7、图10-8中虚线表示的攻击时间协同制导律的控制量为初始控制量，基于MPSP理论对初始控制量不断调整，最后实现了对末端攻击角度的约束。而且，MPSP理论的思路就是要满足末端约束且控制能量最小，所以图10-7、图10-8中MPSP协同制导律下的控制量变化比较平缓，更易于工程实现。
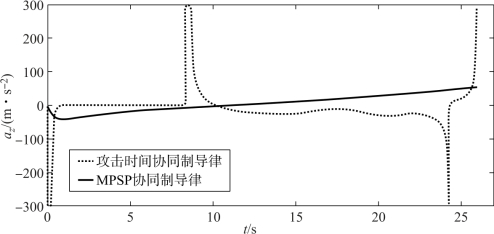
图10-8 控制量az的变化曲线
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同制导与控制的防御弹单向协同制导律详细阅读
针对如式所示的目标信息单向传输时的模型，类似地设计协同拦截制导律。例14-1假设目标、防御弹和攻击弹的初始位置、速度和弹道倾角同例13-1中的表13-1，3个飞行器常速飞行，攻击弹和防御弹分别采用Nm=4、Nd=4的增强比例导引律。图14-6不同防御弹制导律时qmd的变化曲线图14-7不同防......
2023-08-02
-
多飞行器协同制导与控制：附加制导指令确定详细阅读
本节阐述如何确定满足攻击时间要求的附加指令uF。联立式、式，可以得到加速度指令，也就是基于线性模型得出的ITCG导引律，为由式可知，当导弹接近目标时，xgo趋于0，此时上述制导指令会趋于无穷大。表8-14枚导弹的初始参数图8-3给出了4枚导弹采用PNG和ITCG时的弹道对比。在采用PNG时，导弹1、导弹2、导弹3和导弹4的攻击时间分别为35.67 s、30.83 s、27.40 s和31.89 s，4枚导弹采用PNG时的攻击时间差较大，最大攻击时间差为8.27 s。......
2023-08-02
-
信息与控制: 多飞行器协同制导详细阅读
信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致，必须存在一个各导弹共同关心的变量，这称为信息状态。此外，还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法，这称为一致性算法。因此，可将一致性理论应用于多导弹编队，基于一致性算法来设计导弹的编队控制算法。......
2023-08-02
-
多飞行器协同制导与控制技术详细阅读
多飞行器协同飞行，当攻击目标时，如果能够从不同的方向同时命中目标，则能够大大提高对目标的攻击性能。要想实现此目的，需有协同末制导律作为技术支撑。进一步，在设计协同末制导律时，还需考虑各导弹的控制量受限、框架角受限等约束问题。对于通过信息传输实现协同攻击的多导弹，信息的传输模式、通信拓扑的设定和信息的利用规则是设计协同末制导律的关键问题。......
2023-08-02
-
多飞行器协同制导：攻击时间和角度约束制导律详细阅读
本章在此基础上，考虑攻击角度的约束，给出能够同时实现攻击时间约束和攻击角度约束的末制导律。因此，导弹在预测时采用三维制导律表达式为不同于文献[58]中通过纵向弹道的调整来实现攻击时间约束，本章通过在侧向制导指令中加入理想攻击时间与预测攻击时间的误差作为反馈项来实现对攻击时间的控制，而在纵向采用式所示的偏置比例导引律来实现对攻击落角的控制。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
多飞行器协同制导求解详细阅读
由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。......
2023-08-02
相关推荐