虚拟领弹运动及从弹协同策略关键参数——多飞行器协同制导与控制

2023-08-02 理论教育版权反馈

【摘要】：为使er→0，即＜0，最好Vm＞Vl，即虚拟领弹的速度小于从弹速度。所以需设置er=r-rl＞0，即从弹位置较远，需先追赶虚拟领弹，通过合理设计参数kr，飞行中后期进行小范围机动缩小弹目距离偏差，令速度前置角常处于非饱和状态，此时飞行剩余距离较短，协同效果较好。综上所述，虚拟领弹运动参数需满足式中，下标为“0”表示此为初始时刻的值。根据式设计虚拟领弹的初始条件，可使协同策略中的脱靶量较小，时间协同效果较好。

设当前导弹的弹目距离与虚拟领弹弹目距离的差为er，er=r-rl。对其求导，并考虑式（10-18）中弹目距离变化率的表达式，可得

式中，下标为“l”表示此处为虚拟领弹的量；第二项和第四项是关于目标速度的乘积项，因目标速度较小，可以忽略。

为使er→0，即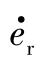 pagenumber_ebook=149,pagenumber_book=140 ＜0，最好Vm＞Vl，即虚拟领弹的速度小于从弹速度。如果有i枚导弹参与协同作战，粗略地估计导弹i的攻击时间≈ri0/Vmi（ri0为导弹i的初始弹目距离，Vmi为导弹i的速度），由于还需为后续调整角度留出足够的调整裕度，因此设计的协同攻击时间t*（即虚拟领弹的攻击时间）应满足

式中，tl——虚拟领弹攻击目标的时间；

　　　tgi——第i枚导弹为调整攻击角度留出的时间裕度；

　　　rl0——虚拟领弹的初始弹目距离；

　　　maxi（ pagenumber_ebook=149,pagenumber_book=140 +tgi）——所有参与协同作战导弹的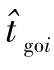+tgi的最大值。

分析式（10-32）可知，当初始时刻er＜0时，从弹的弹目距离小，需进行一定机动绕弯以等待虚拟领弹，如果从弹绕弯飞行路程比较长，那么从弹的速度可能衰减至小于虚拟领弹的飞行速度，在弹道末段可能会出现长时间以速度前置角η=0°飞行但仍无法跟踪上虚拟领弹的弹目距离变化的情况，此时协同效果不好。所以需设置er=r-rl＞0，即从弹位置较远，需先追赶虚拟领弹，通过合理设计参数kr，飞行中后期进行小范围机动缩小弹目距离偏差，令速度前置角常处于非饱和状态，此时飞行剩余距离较短，协同效果较好。

综上所述，虚拟领弹运动参数需满足

式中，下标为“0”表示此为初始时刻的值。

根据式（10-34）设计虚拟领弹的初始条件，可使协同策略中的脱靶量较小，时间协同效果较好。初始猜测控制解设计得合理，会为后续MPSP算法实现对攻击角度的约束奠定良好的基础，会减少MPSP算法的迭代次数，加快其收敛速度。

受框架角等因素约束，导弹的速度前置角应在一定范围内变化，即ηψ∈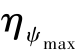（ pagenumber_ebook=150,pagenumber_book=141 为允许的最大速度前置角），考虑到此约束，协同过程中应尽可能使速度前置角指令ηψc∈[0，ηmax]。在基于弹目距离跟踪的攻击时间协同策略中，参数kr影响着弹目距离误差的收敛速度，对协同的成功与否起决定性作用。若kr大，则弹目距离误差收敛得快；反之，收敛得慢。但若kr选取过大，很小的弹目距离差就会引起很大的速度前置角指令，就可能使ηψc长时间处于极值（ηmax或0），从而导致协同失败；若kr取值过小，则速度前置角指令对弹目距离差的敏感度就会很低，就可能出现很长时间也不能实现协同的情况。因此，应根据弹群协同作战的初始条件对参数kr进行合理预估。由于希望

因此将初始时刻的参数代入式（10-35），得到初始状态下kr的选取范围，然后在此范围内适当取值。对于参与协同作战的多枚导弹来讲，参数的设计方法相同。例如，末制导开始时，各弹的初始状态差异不大，可用相同的kr；但若差异较大，则应分别设计协同策略中的kr。

虚拟领弹运动及从弹协同策略关键参数——多飞行器协同制导与控制

相关推荐