首页理论教育协同制导与控制：三维空间导弹-目标运动模型

协同制导与控制：三维空间导弹-目标运动模型

2023-08-02 理论教育版权反馈

【摘要】：导弹在三维空间攻击目标的相对运动关系如图10-1所示。图10-1三维空间导弹-目标导引几何关系假设目标仅在水平方向运动，则三维空间弹目相对运动方程组为导弹在地面坐标系中的运动学方程组为式中，xm，ym，zm——导弹质心在地面坐标系三轴的投影。如果各导弹的理想攻击时间t*相同，则多枚导弹能够实现在同一时刻从不同的指定方向命中目标。

导弹在三维空间攻击目标的相对运动关系如图10-1所示。图中，Axyz是地面惯性坐标系；M与T分别表示导弹与目标；r为弹目距离；qθ和qψ分别为俯仰方向和偏航方向的视线角；Vm、θm和ψVm分别为导弹的速度、弹道倾角与弹道偏角；Vt、θt和ψVt分别为目标的速度、弹道倾角与弹道偏角。图中所示均为角度的正方向。

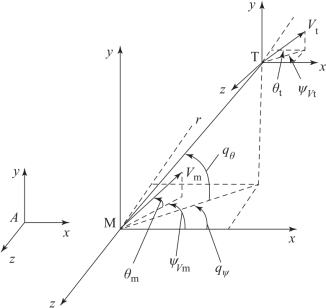
pagenumber_ebook=145,pagenumber_book=136

图10-1　三维空间导弹-目标导引几何关系

假设目标仅在水平方向运动（即θt=0），则三维空间弹目相对运动方程组为

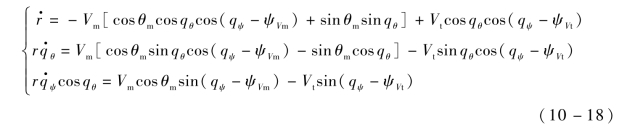
pagenumber_ebook=145,pagenumber_book=136

导弹在地面坐标系中的运动学方程组为

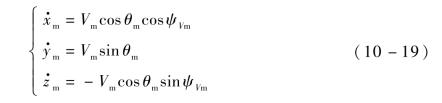
pagenumber_ebook=145,pagenumber_book=136

式中，xm，ym，zm——导弹质心在地面坐标系三轴的投影。

将导弹视为质点，导弹的动力学方程组为

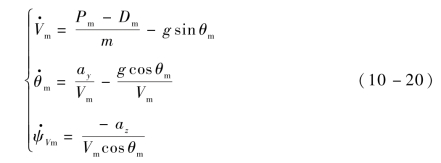
pagenumber_ebook=145,pagenumber_book=136

式中，Pm——推力；

　　　Dm——阻力；

　　　m——导弹质量；

　　　ay，az——导弹俯仰方向和偏航方向的法向加速度。

假设导弹自动驾驶仪模型为

pagenumber_ebook=146,pagenumber_book=137

式中，τ——自动驾驶仪时间延迟系数；

　　　ayc，azc——y、z方向的指令加速度。

由于本章假设目标在水平面运动，因此其运动模型为

pagenumber_ebook=146,pagenumber_book=137

式中，azt——目标的法向加速度；

　　　xt，zt——目标质心在水平面内的位置坐标。

联立式（10-19）、式（10-20），可得在地面坐标系下导弹的三维运动模型为

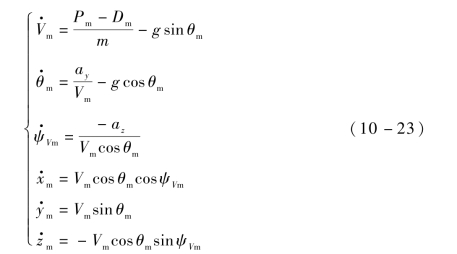
pagenumber_ebook=146,pagenumber_book=137

令X=[Vm θm ψVm xm ym zm]T为导弹的状态变量，U=[ay az]T为控制变量，对状态变量和控制变量进行归一化处理，可得

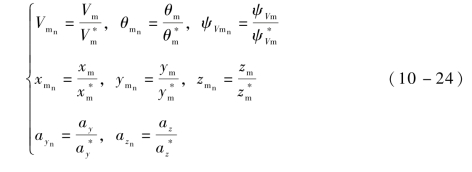
pagenumber_ebook=146,pagenumber_book=137

式中，带下标“n”的量表示归一化后的变量；带上标“*”的量表示归一化的参考数值。

归一化后的导弹运动方程组可写为

pagenumber_ebook=147,pagenumber_book=138

类似地，将目标运动方程组进行归一化处理，可得

pagenumber_ebook=147,pagenumber_book=138

针对如式（10-25）所示的导弹非线性运动模型，选取输出变量Y=。给定多导弹的协同攻击时间Td=t*，假设仿真时末端终止时间步数为N，根据脱靶量和攻击角度约束，给定理想的末端输出变量。协同制导律的设计目标：通过设计控制变量，使得在t*时刻各导弹的输出Y能够趋近于理想的输出变量，即满足末端约束。如果各导弹的理想攻击时间t*相同，则多枚导弹能够实现在同一时刻从不同的指定方向命中目标。