【摘要】:而且,如果各导弹的rc相同,而各导弹的弹目距离能够跟踪rc,那么在飞行过程中,多枚导弹将同步接近目标,实现位置协同。为控制弹目距离跟踪式(9-7)给定的弹目距离指令,实现多导弹的弹目距离协同,只需设计制导律u,并控制导弹的速度前置角跟踪导弹前置角指令σc。
为满足弹群同时到达目标的协同任务需求,在文献[53]的基础上设计各枚导弹的弹目距离指令为
式中,μ,V′——待设计的参数,μ>0,V′>0;
Td——期望的攻击时间;
t——当前飞行时间。
由式(9-7)可知,当t=Td时,有rc=0,因此多枚导弹能够在t=Td时同时命中目标。而且,如果各导弹的rc相同,而各导弹的弹目距离能够跟踪rc,那么在飞行过程中,多枚导弹将同步接近目标,实现位置协同。与文献[53]直接设计制导律跟踪rc的研究方法不同,本章进一步将弹目距离跟踪控制问题转化为导弹速度前置角跟踪控制,避免了文献[53]中的控制器奇异问题。
首先,定义弹目距离跟踪误差
对其求导并将式(9-1)代入,可得
式中,σc——待设计的导弹速度前置角指令。
为使er→0,可设计
式中,kr>0,代入式(9-9),可得
因此,将有er→0。为控制弹目距离跟踪式(9-7)给定的弹目距离指令,实现多导弹的弹目距离协同,只需设计制导律u,并控制导弹的速度前置角跟踪导弹前置角指令σc。
由于式(9-10)的右端需满足范围[1,1],且导弹-目标的相对速度应小于零,σc的取值范围应满足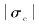 ∈[0,σmax](σmax为最大允许速度前置角,0<σmax<π/2),同时,为了命中目标,需有σc=0。因此,为保证命中目标,实现弹目距离协同、攻击时间协同,完成高效的信息化饱和攻击,可将式(9-10)所示的算法改进为
∈[0,σmax](σmax为最大允许速度前置角,0<σmax<π/2),同时,为了命中目标,需有σc=0。因此,为保证命中目标,实现弹目距离协同、攻击时间协同,完成高效的信息化饱和攻击,可将式(9-10)所示的算法改进为
式中,σ0——速度前置角的非零初始值,若σ0=0,则此处的符号取正或负均可;
rε——某一设定的较小的弹目距离。
当弹目距离不小于rε且(kr er- )/V≤-1时,说明当前的弹目距离小于期望的弹目距离很多,导弹的相对速度需要大幅减小以趋于期望弹目距离,但受到最大速度前置角的约束,速度前置角指令最大只能取σmax,符号则与初始速度前置角σ0的符号相同;当弹目距离r不小于rε,且
)/V≤-1时,说明当前的弹目距离小于期望的弹目距离很多,导弹的相对速度需要大幅减小以趋于期望弹目距离,但受到最大速度前置角的约束,速度前置角指令最大只能取σmax,符号则与初始速度前置角σ0的符号相同;当弹目距离r不小于rε,且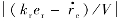 <1时,导弹速度前置角指令取arccos(kr er-
<1时,导弹速度前置角指令取arccos(kr er-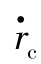 )/V即可,通过适当调节相对速度来使弹目距离跟踪期望弹目距离;当r≥rε且(kr er-
)/V即可,通过适当调节相对速度来使弹目距离跟踪期望弹目距离;当r≥rε且(kr er-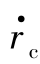 )/V≥1时,在式(9-12)中,属于“其他”的情况,有σc=0,此时导弹的弹目距离远大于期望弹目距离,因此导弹需以最大的相对速度飞行、接近目标,以尽快减小弹目距离,趋近于期望弹目距离。当弹目距离r<rε时,说明导弹距离目标比较近,此时令σc=0,即使导弹的速度方向与视线重合(实际为追踪法),以便较好地攻击目标,需要说明的是,此时制导指令不再是协同指令,但由于导弹前期按照协同指令飞行且rε比较小,因此后期的追踪法对理想攻击时间的实现影响不大。
)/V≥1时,在式(9-12)中,属于“其他”的情况,有σc=0,此时导弹的弹目距离远大于期望弹目距离,因此导弹需以最大的相对速度飞行、接近目标,以尽快减小弹目距离,趋近于期望弹目距离。当弹目距离r<rε时,说明导弹距离目标比较近,此时令σc=0,即使导弹的速度方向与视线重合(实际为追踪法),以便较好地攻击目标,需要说明的是,此时制导指令不再是协同指令,但由于导弹前期按照协同指令飞行且rε比较小,因此后期的追踪法对理想攻击时间的实现影响不大。
由式(9-12)可见,前置角指令可能存在跳变,其导数可能出现无穷大或很大的情况,考虑到控制系统的实现问题,采用如下的指令成型低通滤波器对式(9-12)进行滤波:
式中,τσ——滤波器时间常数。为保证导弹速度前置角期望值σd快速且稳定地跟踪式(9-12),应将τσ设计得较小。
综上设计与分析可以看出,为实现弹目距离协同、攻击时间协同并命中目标,制导律的设计目标是:寻找控制器u,使得导弹的速度前置角跟踪导弹的速度前置角期望值σd,并保证控制器u满足式(9-4)给出的约束条件。

 )/V≤-1时,说明当前的弹目距离小于期望的弹目距离很多,导弹的相对速度需要大幅减小以趋于期望弹目距离,但受到最大速度前置角的约束,速度前置角指令最大只能取σ
)/V≤-1时,说明当前的弹目距离小于期望的弹目距离很多,导弹的相对速度需要大幅减小以趋于期望弹目距离,但受到最大速度前置角的约束,速度前置角指令最大只能取σ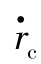 )/V即可,通过适当调节相对速度来使弹目距离跟踪期望弹目距离;当r≥r
)/V即可,通过适当调节相对速度来使弹目距离跟踪期望弹目距离;当r≥r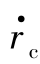 )/V≥1时,在式(9-12)中,属于“其他”的情况,有σ
)/V≥1时,在式(9-12)中,属于“其他”的情况,有σ







相关推荐