基于人工势场和信息一致性的防碰撞方法

2023-08-02 理论教育版权反馈

【摘要】：当rij≤rmin时，，此时编队指令ui基本上不起作用，导弹主要以避撞为主。式（7-8）表示考虑了碰撞避免问题的编队方法。当F1和F5之间的距离大于安全距离后，人工势场作用消失，导弹在一致性编队指令的作用下，最终形成编队。进一步考虑导弹位置的平滑变化，可将两枚导弹间距离的变化率考虑到人工势场的设计中。本章只将人工势场与一致性算法相结合，实现了多导弹编队过程中避免碰撞的基本思路和概念，进一步的研究，读者可自行进行。

为了研究问题的明确性，本章不考虑分布式飞行飞行器间的通信约束问题，即假设多飞行器间的通信是理想的。在第6章中，基于一致性算法设计了可实现多导弹编队飞行的方法，但是其无法保证在队形形成过程（算法收敛过程）中，导弹与导弹之间的距离不出现≤rmin的情况。因此，可在一致性编队指令的基础上附加与相对距离相关的人工势场力，当弹间距rmin＜rij≤ρ时，开始有排斥力产生，阻止两弹靠近；当rij≤rmin时，排斥力为无穷大；当两弹的距离到达安全距离后，排斥力消失，导弹继续在一致性编队指令的作用下飞行，以形成编队。

导弹i受到的人工势场力总和为Fi，由其引起的指令加速度为

pagenumber_ebook=109,pagenumber_book=100

式中，mi——导弹i的质量。

综合一致性编队算法和人工势场防碰撞算法，可得导弹的指令加速度为

式中，ui——第6章中得到的一致性编队算法，即式（6-18）。当弹间距离大于等于安全距离ρ时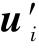， pagenumber_ebook=109,pagenumber_book=100 =0，只有一致性编队指令作用，导弹朝着形成编队的方向飞行。当处于rmin＜rij≤ρ时，ui和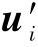均不等于零，导弹在两者同时作用下飞行。当rij≤rmin时，，此时编队指令ui基本上不起作用，导弹主要以避撞为主。

式（7-8）表示考虑了碰撞避免问题的编队方法。

例7-1　假设有1枚虚拟领弹（VL）和6枚从弹（F1～F6），它们之间的通信拓扑如图7-2所示，初始队形如图7-3所示。假设需要进行队形变换，变换后的队形如图7-4所示。

pagenumber_ebook=109,pagenumber_book=100

图7-2　通信拓扑

pagenumber_ebook=109,pagenumber_book=100

图7-3　初始队形

pagenumber_ebook=109,pagenumber_book=100

图7-4　期望队形

由图7-2可知，邻接矩阵A7= pagenumber_ebook=109,pagenumber_book=100

由图7-4可知，期望队形参数（各方向的单位均为米（m））如下：

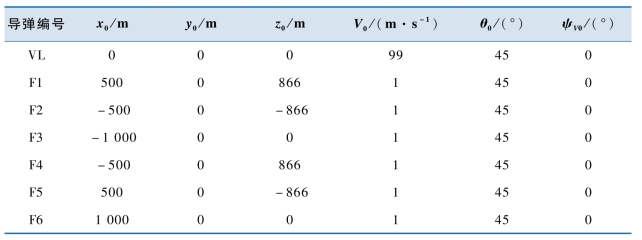
pagenumber_ebook=110,pagenumber_book=101

虚拟领弹的速度为ζ7=[70 70 0]T（m/s，m/s，m/s），虚拟领弹和各从弹的初始状态见表7-1，表中下标“0”表示初始时刻。

表7-1　多导弹初始状态

pagenumber_ebook=110,pagenumber_book=101

一致性编队算法（式（6-18））中的γ0=0.2、γ1=0.4，式（7-6）中的系数Kr=108，最小安全距离rmin=30 m，安全距离ρ=320 m，各导弹的最大切向加速度和法向加速度分别为40 m/s2、60 m/s2和60 m/s2。设从弹的最大速度为150 m/s。仿真结果如图7-5～图7-8所示。

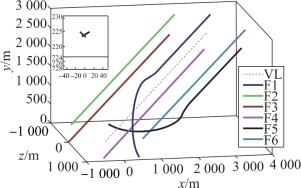
pagenumber_ebook=110,pagenumber_book=101

图7-5　无人工势场时的三维轨迹

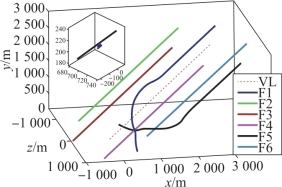
pagenumber_ebook=110,pagenumber_book=101

图7-6　有人工势场时的三维轨迹

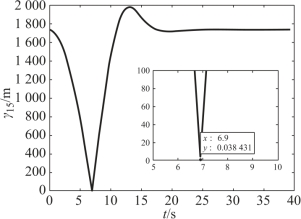
pagenumber_ebook=111,pagenumber_book=102

图7-7　无人工势场时的γ15变化曲线

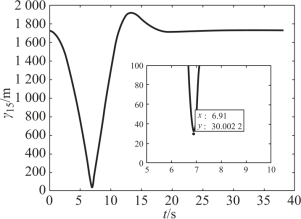
pagenumber_ebook=111,pagenumber_book=102

图7-8　有人工势场时的γ15变化曲线

由初始位置和期望队形可知，队形变换需要F1和F5对调位置；由图7-5、图7-6可知，在无人工势场指令和有人工势场指令的情况下，导弹最后都形成了指定的队形。但是，在无人工势场指令时，两枚导弹之间的最小间距小于0.05 m（图7-7），这远小于最小安全距离，故可视为已经发生了碰撞。当加了人工势场力之后，F1和F5的最小距离大于30 m，满足最小安全距离的要求，避免了碰撞，如图7-8所示。当F1和F5之间的距离大于安全距离后，人工势场作用消失，导弹在一致性编队指令的作用下，最终形成编队。

需要说明的是，在本实例中，只有F1和F5之间的距离出现了小于安全距离320 m的情况，其他导弹与导弹间的距离均大于320 m，因此人工势场力作用只存在于F1和F5之间，是一种比较简单的情况。另外，安全距离决定了人工势场力在什么时候开始起作用，只有合理设置它和人工势场力中的相关参数（如系数Kr），才能使弹间的最小距离大于最小安全距离，从而避免弹间碰撞。本章中的人工势场只与弹间的距离有关，弹间距离近，势场力就大，反之则小。此时，可能造成导弹位置的振荡。进一步考虑导弹位置的平滑变化，可将两枚导弹间距离的变化率考虑到人工势场的设计中。例如，在安全距离内，若弹间距离变化率大于0，则说明弹间距离在变大，此时的人工势场指令可小些；若弹间距离变化率小于0，则说明弹间距离在变小，在朝着更危险的方向变化，此时的人工势场指令可大些。本章只将人工势场与一致性算法相结合，实现了多导弹编队过程中避免碰撞的基本思路和概念，进一步的研究，读者可自行进行。

基于人工势场和信息一致性的防碰撞方法

相关推荐