首页理论教育通信噪声的改进一致性编队算法：飞行器协同制导与控制

通信噪声的改进一致性编队算法：飞行器协同制导与控制

2023-08-02 理论教育版权反馈

【摘要】：通常的一致性编队算法中，控制参数γ0、γ1均为常值，在本节中，为了减弱噪声对多飞行器系统编队的影响，令γ1随时间变化，对γ1进行设计，得到改进的一致性编队算法。，n，j=1，2）恒成立，故该领导跟随结构多飞行器系统在存在通信噪声的情况下采用式所示的一致性编队算法，误差系统能够收敛。图6-13改进一致性算法下的导弹位置跟踪误差变

6.3.2.1　算法设计及收敛性证明

为了减弱噪声对多飞行器系统编队飞行的影响，对以下一致性编队算法进行改进设计：

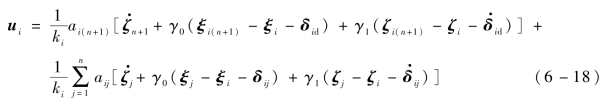
pagenumber_ebook=97,pagenumber_book=88

式中，ki——从弹i的入度，ki=

　　　γ0，γ1——待设计的控制参数；

　　　δid，δij——由期望队形确定，δij=δid-δjd。

对比式（6-18）和式（6-13）所示的一致性编队算法，其区别在于式（6-18）中加入了领弹和从弹j的加速度信息。根据文献[47]，在领弹和从弹间的通信拓扑存在有向生成树时，式（6-18）能够使从弹的位置和速度收敛，从而形成编队。在本节中，由于问题的焦点在于研究通信噪声对收敛性和收敛精度的影响，因此为了研究问题的方便，假设队形δid=δjd=0。通常的一致性编队算法中，控制参数γ0、γ1均为常值，在本节中，为了减弱噪声对多飞行器系统编队的影响，令γ1随时间变化，对γ1进行设计，得到改进的一致性编队算法。

将含有噪声信息的式（6-16）、式（6-17）代入式（6-18），可得

pagenumber_ebook=98,pagenumber_book=89

Q中包含了领弹和从弹的状态信息和通信拓扑中的噪声信息，各导弹的状态信息是有界的，通信噪声通常也是有界的，故Q有确定的上界，即‖Q‖≤K（K为Q的上界常数矩阵），也就是Qij≤Kij（i=1，2，…，2n，j=1）。要证明式（6-21）所示的多飞行器误差系统的收敛性，则在Q有界的条件下只需证明矩阵Γ的特征值在复平面的负半平面即可。矩阵Γ的特征多项式为

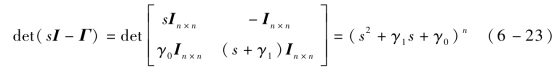
pagenumber_ebook=98,pagenumber_book=89

令det（s I-Γ）=0，则

所以Γ的两个特征值λi1、λi2（i=1，2，…，n，n维重根）分别为

pagenumber_ebook=99,pagenumber_book=90

由于γ0＞0、γ1＞0，因此，Reλij＜0（i=1，2，…，n，j=1，2）恒成立，故该领导跟随结构多飞行器系统在存在通信噪声的情况下采用式（6-19）所示的一致性编队算法，误差系统能够收敛。但是，通信噪声的存在会影响误差系统的稳态收敛值。接下来，讨论式（6-19）中的控制参数对稳态收敛误差的影响。

6.3.2.2　算法参数对稳态收敛误差的影响

对式（6-20）进行拉普拉斯变换，可得

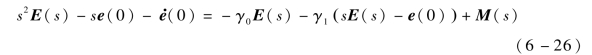
pagenumber_ebook=99,pagenumber_book=90

式中，e（0）——e在t=0时刻的初始值。

假设通信噪声为常值噪声，即αij=k1、βij=k2（i，j=1，2，…，n+1，k1、k2为常数），当通信拓扑和控制参数一定时，M为常值矩阵，此时其拉普拉斯变换为M（s）=M/s，则式（6-26）可以化简为

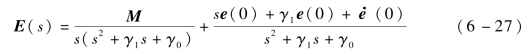
pagenumber_ebook=99,pagenumber_book=90

由终值定理可得

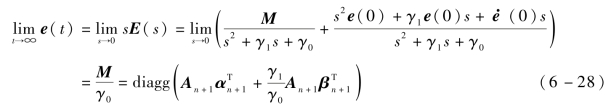
pagenumber_ebook=99,pagenumber_book=90

由式（6-28）可知，位置收敛总误差e与领弹与从弹之间的噪声信息、从弹之间的噪声信息以及控制参数γ0和γ1有关，可以通过设计控制参数γ0、γ1来减小位置收敛总误差。假设γ0不变，增大γ1，由式（6-26）可见，收敛速度加快，但收敛后总误差也增大；反之，减小γ1，收敛速度减慢，收敛后总误差也减小，从而提高了收敛精度。因此，设γ0为常数，设计γ1为

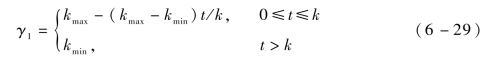
pagenumber_ebook=99,pagenumber_book=90

式中，kmax，kmin，k——常数。

按照式（6-29）设置的γ1在前期较大，可以使一致性算法快速收敛；在后期较小，可以保证良好的收敛精度。

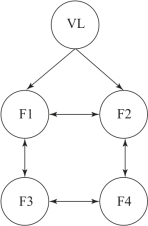
pagenumber_ebook=100,pagenumber_book=91

图6-8　多导弹间的通信拓扑

例6-2　假设1枚虚拟领弹和4枚从弹编队飞行，此处为了更方便地显示通信噪声的影响，仍然忽略导弹的队形参数，使得从弹和领弹的飞行轨迹一致（若考虑队形，只需按照队形要求赋予δid和δjd一定的值）。虚拟领弹（VL）和从弹（F1～F4）之间的通信拓扑如图6-8所示。

图中，通信拓扑中的通信权值取1。由图6-8可得到从弹（F1～F4）的邻接矩阵和拉普拉斯矩阵分别为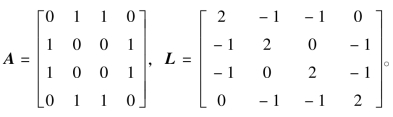 pagenumber_ebook=100,pagenumber_book=91 虚拟领弹（VL）与从弹（F1～F4）的邻接矩阵D=diag（1，1，0，0）。以各导弹的x方向为例，假设从弹（F1～F4）的初始位置、速度（ξ，ζ）分别为（1，0）、（2，0）、（3，0）、（4，0）。领弹的初始状态为（ξ5，ζ5）=（0，0）、加速度为u5=-sin t。假设常值噪声αij=βij=0.2（i，j=1，2，…，n+1）。在协同一致性编队算法中，控制参数γ0=γ1=10，仿真结果如图6-9、图6-10所示。图6-10中的ex表示位置跟踪误差。

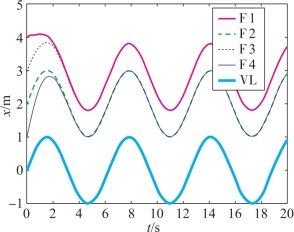
pagenumber_ebook=100,pagenumber_book=91

图6-9　γ0=γ1=10时的多导弹位置状态

pagenumber_ebook=100,pagenumber_book=91

图6-10　γ0=γ1=10时的多导弹位置跟踪误差变化曲线

由图6-9、图6-10可知，由于通信噪声干扰的存在，多导弹的位置并未收敛到一致，从弹始终与领弹的位置存在一定的稳态误差。针对F1，由第二部分的定义可得，ex1=a12（ξ1-ξ2）+a13（ξ1-ξ3）+a14（ξ1-ξ4）+a15（ξ1-ξ5），代入通信权值可得ex1=（ξ1-ξ2）+（ξ1-ξ3）+（ξ1-ξ5）。由终值定理推导，得出ex1=a12α12+a13α13+a14α14+a15α15+（a12β12+a13β13+a14β14+a15β15），代入噪声数值、通信权值和控制参数，可得ex1=1.2，即ex1=（ξ1-ξ2）+（ξ1-ξ3）+（ξ1-ξ5）=1.2。同理，可得ex2=（ξ2-ξ1）+（ξ2-ξ4）+（ξ2-ξ5）=1.2、ex3=（ξ3-ξ1）+（ξ3-ξ4）=0.8、ex4=（ξ4-ξ2）+（ξ4-ξ3）=0.8。由ex1=ex2，可得ξ1=ξ2；由ex3=ex4，可得ξ3=ξ4。将ξ3=ξ4代入ex3，可得ξ3-ξ1=0.8，即ξ4-ξ2=0.8。将ξ1=ξ2、ξ3-ξ1=0.8代入ex1，得到ξ1-ξ5=2，故ξ3-ξ5=2.8。图6-10显示了上述结论。

由式（6-28）可知，减小γ1/γ0能够减小收敛误差，令控制参数γ0=10、γ1=1.5，仿真结果如图6-11、图6-12所示。

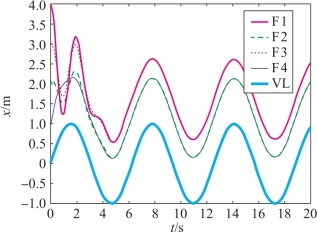
pagenumber_ebook=101,pagenumber_book=92

图6-11　γ0=10、γ1=1.5时的多导弹位置状态

pagenumber_ebook=101,pagenumber_book=92

图6-12　γ0=10、γ1=1.5时的多导弹位置跟踪误差变化曲线

由图可知，γ1的减小使得收敛误差减小，但是其收敛速度变慢。接下来，仍然令γ0=10，γ1如式（6-29）变化（kmax=10，kmin=1.5，k=3），仿真结果如图6-13所示。以F3的位置跟踪误差为例，γ0=10，γ1分别为10、1.5和按照式（6-29）变化（改进一致性算法）时的结果如图6-14所示，图中ex3表示F3的位置跟踪误差。

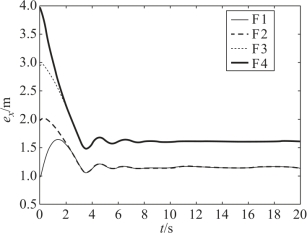
pagenumber_ebook=102,pagenumber_book=93

图6-13　改进一致性算法下的导弹位置跟踪误差变化曲线

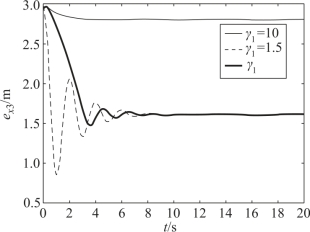
pagenumber_ebook=102,pagenumber_book=93

图6-14　不同γ1时F3的位置跟踪误差变化曲线

对比图6-13与图6-10，相比γ1=10的情况，引入时变控制参数的改进一致性算法的收敛误差有了较大幅度的减小，F1、F2的位置跟踪误差减小到1.2左右，F3、F4的位置跟踪误差减小到1.6左右，减小了收敛总误差。由图6-14可知，γ1=10时，F3的位置跟踪误差较快收敛至2.8附近；γ1=1.5时，F3的位置跟踪误差经过较大幅度的振荡与调整，慢慢收敛至1.6左右；当γ1采用设计的时变控制参数时，收敛速度较γ1=1.5时有所提升，收敛误差比γ1=10时小，收敛过程更加平滑，即改进的一致性算法能够使前期的收敛速度较快、后期的收敛误差较小，在满足收敛速度的前提下达到了降噪的目的。