【摘要】:信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致,必须存在一个各导弹共同关心的变量,这称为信息状态。此外,还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法,这称为一致性算法。因此,可将一致性理论应用于多导弹编队,基于一致性算法来设计导弹的编队控制算法。
近些年,多飞行器的协作和协同控制问题得到了广泛关注,多智能体一致性理论的提出为多飞行器实现群集、编队、协同提供了有效的途径。在实际应用中,多导弹要形成编队,即要保持它们之间的相对状态不变。当多个导弹对所关心的变量或者状态的取值达成共识时,就称它们已经达成“一致”。信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致,必须存在一个各导弹共同关心的变量,这称为信息状态。此外,还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法,这称为一致性算法。信息状态表达了导弹编队协同变量的实际含义,如编队的中心位置(或队形)、编队集结时间、飞行区域的大小、多导弹群运动的方向、军事目标的毁伤概率等。
由于假设各导弹基于其相邻导弹的信息状态来更新自己的信息状态,因此面临的问题就是如何设计一个更新律,使得网络中所有导弹的信息状态收敛于一个共同值。
传统的连续时间一致性算法描述为
式中,aij——t时刻关于通信拓扑图Gn的邻接矩阵An的第(i,j)项;
xi——第i枚导弹的信息状态。
于是,借助式(6-11),对任一初始时刻的xi(0)和所有i,j=1,2,…,n,当t→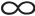 时,有xi(t)→xj(t),即称系统的状态达到一致。
时,有xi(t)→xj(t),即称系统的状态达到一致。
基于图论的一致性算法使得顶点的状态x趋于一致,对于多导弹编队而言,编队飞行时,各导弹的速度大小和方向应一致,且导弹间的距离趋于期望队形指定的距离。因此,可将一致性理论应用于多导弹编队,基于一致性算法来设计导弹的编队控制算法。

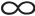 时,有x
时,有x






相关推荐