首页理论教育多飞行器协同控制成果

多飞行器协同控制成果

2023-08-02 理论教育版权反馈

【摘要】：在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。

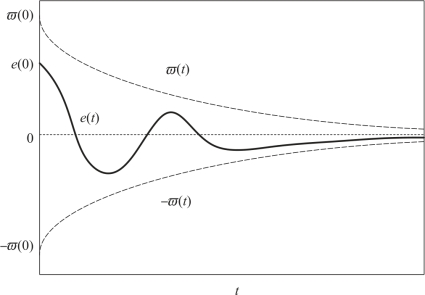
在预设性能控制理论中，通过合理设置性能函数 pagenumber_ebook=69,pagenumber_book=60 （t），控制器可保证稳态时跟踪误差e（t）收敛到一个预先设定的区域，且其瞬态性能（误差大小及收敛速度、超调量）同样满足预设的与性能函数相关的条件。在预设性能控制器的作用下，跟踪误差与性能函数的关系曲线如图5-1所示。

pagenumber_ebook=69,pagenumber_book=60

图5-1　跟踪误差与性能函数的关系曲线

为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。

针对多弹编队飞行问题，假设理想的队形为=[hxi hyi hzi ]T，则系统跟踪误差为e1=[ex ey ez ]T=X1-，通过设计合理的性能函数，可对相对位置误差e1的性能进行预设，从而实现在编队的同时能满足在队形形成过程中避免碰撞。可定义在三个方向上大于0且严格递减的性能函数分别为

pagenumber_ebook=70,pagenumber_book=61

当不等式成立时，误差e1（t）将在函数 pagenumber_ebook=70,pagenumber_book=61 1（t）和-1（t）的夹逼作用下收敛到一个0的小邻域内。

为了降低处理不等式的难度，在系统设计中，通过引入误差变换函数ftran（·）来将不等式约束转为等式约束再进行处理，定义

式中，ε——转换误差。

　　　ftran（ε）满足性质：

①光滑且单调递增。

②-1＜ftran(ε)＜1。

③(ε)=-1，(ε)=1。

针对本问题，选取误差变换函数为

根据ftran（ε）的性质可知，ftran（ε）可逆，则编队跟踪转换误差为

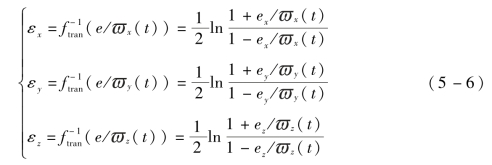
pagenumber_ebook=70,pagenumber_book=61

令ε1=[εxεyεz ]T为转换误差，对ε1进行求导，可得

针对本编队问题，考虑则式（5-7）变为

pagenumber_ebook=71,pagenumber_book=62

设计虚拟控制量X2c为

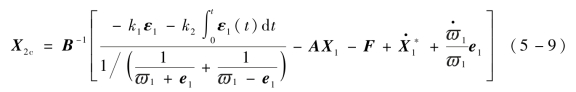
pagenumber_ebook=71,pagenumber_book=62

式中，k1，k2——设计参数。当取k1＞0，k2＞0时，将X2c代入式（5-8），即令式（5-8）中的X2=X2c，可知ε1满足闭环动力学方程因此ε1有界，不等式约束成立，进而跟踪信号满足预设性能要求。

考虑到微分膨胀问题，采用低通滤波器进行滤波，有

pagenumber_ebook=71,pagenumber_book=62

式中，τ——时间常数；

　　　X2d——式（5-1）中第二式中X2需跟踪的量。

设e2=X2-X2d，对其求导，可得

将式（5-1）中的第二式代入式（5-11），采用反演法设计控制器，得到控制量U为