1.终端约束令t0、tf分别为编队形成段的初始时刻与末端时刻，为保证从弹在tf时刻到达指定编队位置，需对从弹在tf时刻的相对位置x、y、z进行约束：式中，x*，y*，z*——从弹在领弹弹道坐标系下的期望编队位置。......
2023-08-02
多飞行器编队性能指标函数
【摘要】：为保证编队尽快形成，同时避免控制量过大，设计性能指标函数为式中，Q——控制加权矩阵，Q∈R3×3；R——终端加权系数。例4-1本实例中，首先给出复合编队策略时的结果，再对单独的动态面编队控制器和复合编队策略控制两种情况进行对比。两枚从弹的相关参数见表4-1，表中的初始相对位置和期望编队位置都是在领弹弹道坐标系中的位置，下标“0”表示初始时刻。导弹采用复合编队策略时的仿真结果如图4-2～图4-10所示。
为保证编队尽快形成，同时避免控制量过大，设计性能指标函数为
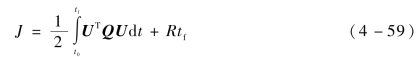
式中，Q——控制加权矩阵，Q∈R3×3；
R——终端加权系数。
综合式（4-31）、式（4-43）～式（4-59），可得到编队形成段理想轨迹生成的最优控制问题。可采用GPOPS工具生成基于高斯伪谱法的理想轨迹。将此理想轨迹作为动态面控制器的待跟踪量（即利用动态面控制器实现对队形形成理想轨迹的跟踪），然后进行队形保持，形成一种复合的编队策略，使得多飞行器能够以尽量短的时间、较少的控制能量形成编队并保持队形飞行，而且能避免队形形成过程中弹间的碰撞。
例4-1 本实例中，首先给出复合编队策略时的结果，再对单独的动态面编队控制器和复合编队策略控制两种情况进行对比。导弹采用单独的动态面控制器时，令理想轨迹X*在整个编队过程中始终保持为从弹的期望编队位置（x*，y*，z*），然后采用DSC控制器对X*进行跟踪，实现编队的形成与保持；当采用复合编队策略时，将基于高斯伪谱法生成的编队形成轨迹作为理想轨迹，利用动态面控制器对此理想轨迹进行跟踪，随后进行编队保持。
假设两枚从弹跟随一枚领弹编队飞行。领弹在惯性坐标系下的初始位置为（0，1 000 m，0），速度、弹道倾角和弹道偏角分别为Vl=200 m/s，θl=0°和ψVl=15°。两枚从弹的相关参数见表4-1，表中的初始相对位置和期望编队位置都是在领弹弹道坐标系中的位置，下标“0”表示初始时刻。
表4-1 两枚从弹的相关参数
表4-2 从弹的状态变量与控制变量约束
动态面参数k1=k2=5，辅助系统参数h1=h2=2，滤波器时间常数τ=0.1 s。在高斯伪谱法中，性能指标权重Q=diag（1，1，1），R=100，两枚从弹之间的最小允许距离ra=100 m。
导弹采用复合编队策略时的仿真结果如图4-2～图4-10所示。
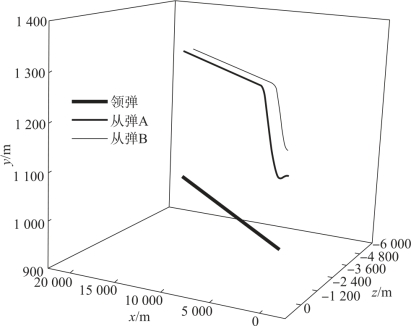
图4-2 导弹三维弹道图
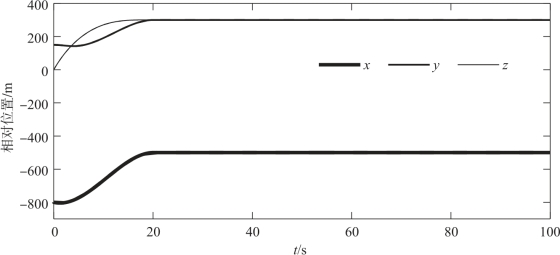
图4-3 从弹A的相对位置变化曲线
图4-4 从弹B的相对位置变化曲线
图4-5 从弹的速度变化曲线
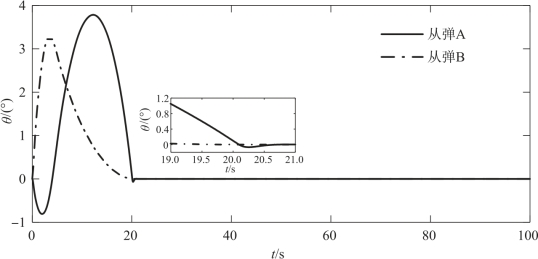
图4-6 从弹的弹道倾角变化曲线
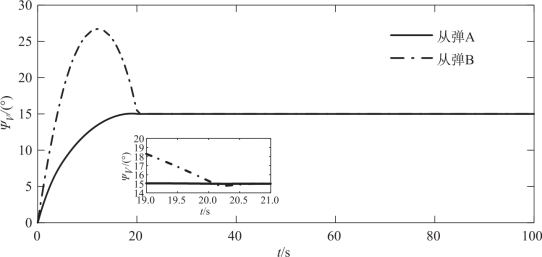
图4-7 从弹的弹道偏角变化曲线
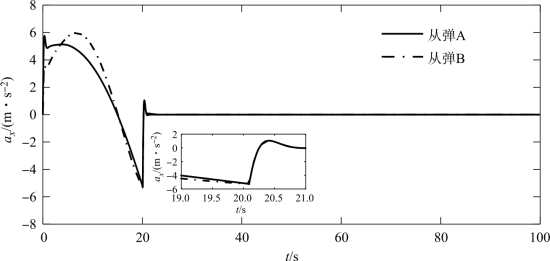
图4-8 从弹的切向加速度ax变化曲线
图4-9 从弹的法向加速度ay变化曲线
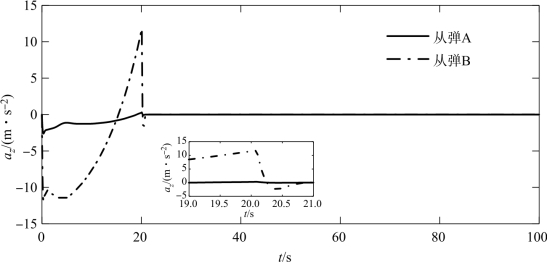
图4-10 从弹的法向加速度az变化曲线
复合编队策略下的编队轨迹如图4-2所示，由图4-3、图4-4可见，在DSC控制器的作用下，两枚从弹的实际运动轨迹实现了对GPM理想轨迹的准确跟踪，而后很好地保持了编队队形，证明了DSC控制器良好的控制精度。编队形成段末端对从弹运动状态的约束，使得在编队形成段与编队保持段衔接处，从弹的运动状态实现光滑过渡，如图4-5～图4-7所示。由于编队形成段从弹实际轨迹可对理想轨迹进行精确跟踪，因此编队形成过程中所需的控制量较小，且从弹运动状态的光滑过渡使得编队形成段向编队保持段过渡过程中所需的控制量较小，随后编队保持过程中的控制量基本为零，如图4-8～图4-10所示。
以从弹A为例，复合编队策略与单独DSC编队策略的仿真结果对比如图4-11～图4-14所示。
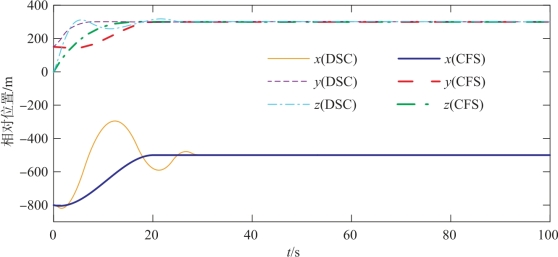
图4-11 两种编队策略时从弹A的相对位置变化曲线
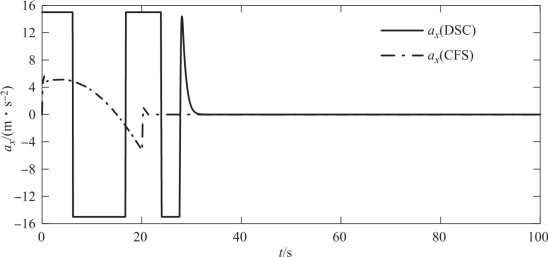
图4-12 两种编队策略时从弹A的切向加速度ax变化曲线
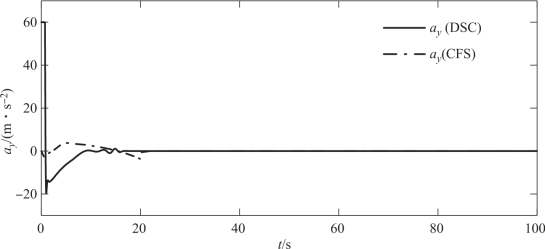
图4-13 两种编队策略时从弹A的法向加速度ay变化曲线
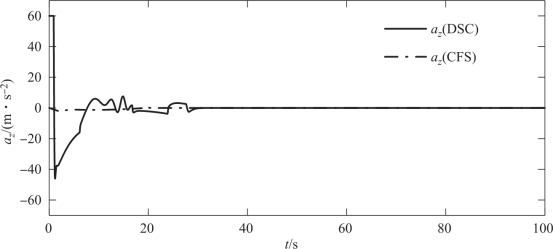
图4-14 两种编队策略时从弹A的法向加速度az变化曲线
由仿真数据可知，复合编队策略下由开始编队到编队队形良好保持共耗时20.4 s，而单独DSC编队策略则需耗时31.2 s，复合编队策略节省了1/3的编队时间，图4-11很好地体现了这一点，这也证明了本章提出的复合编队策略快速形成编队的优点，而节省的编队时间将有利于提高多导弹的协同搜索、协同突防等能力。对于单独DSC编队策略，因从弹的初始相对位置与期望编队位置间存在较大差值，故编队过程需要较大的控制量来实现从弹实际轨迹对理想轨迹的跟踪，如图4-12～图4-14所示；相比之下，复合控制策略所需的控制量则小得多，这将很大程度减少能量的消耗。此外，由于初始编队阶段较大的位置误差及较大的控制量作用，因此在单独DSC编队策略下，从弹的实际相对位置会发生大范围波动（图4-11），这将有可能引起从弹之间发生碰撞；而在复合编队策略下，从弹实际轨迹在精确跟踪理想轨迹后，可有效避免碰撞问题。
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同制导控制的理想通信时一致性编队算详细阅读
假设多导弹间的通信是理想的，选取导弹的位置和速度信息作为协同变量，基于一致性算法来设计多导弹编队控制方法。当时，称多导弹形成了期望的队形，达到了编队一致性。表6-1多导弹初始状态一致性编队算法中的控制参数k′=2，k″=4，各导弹的最大切向加速度和法向加速度分别为40 m/s2、60 m/s2和60 m/s2。......
2023-08-02
-
多飞行器协同制导求解详细阅读
由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。......
2023-08-02
-
多飞行器协同导控技术详细阅读
针对多飞行器协同任务规划问题，常用的模型有混合整数线性规划模型、多旅行商模型、多车辆路由模型、协同多任务规划模型等。通常采用直接法和间接法对航迹规划非线性最优控制问题进行求解，而采用基于几何学的搜索算法对航迹规划空间几何搜索问题进行求解。因此，相对单飞行器的航迹规划问题，多飞行器的协同航迹规划问题具有约束更多且更为复杂的特点。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
多飞行器协同控制成果详细阅读
在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。......
2023-08-02
-
多飞行器协同制导与防御弹2控制详细阅读
在目标、防御弹1和防御弹2协同对攻击弹拦截的过程中，目标和防御弹1采用式所示的协同拦截制导律飞行，防御弹2则跟踪防御弹1的弹目距离，最终实现和防御弹1同时拦截攻击弹。因此，当防御弹1与防御弹2距离攻击弹很近时，令防御弹2转为采用式所示的可实现落角约束的弹道成型制导律。......
2023-08-02
-
多飞行器协同避碰控制策略详细阅读
针对此问题，根据预设性能控制器可将系统误差控制在满足性能函数上下边界范围内的特点，可通过合理地设置性能指标函数来实现弹间的避碰。接下来，将上述性质应用于多弹编队成员间避碰策略的设计中。......
2023-08-02
相关推荐